Измеренных различными методами: Бринелля, Виккерса и Роквелла
| НВ, HV | HRB | 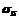 , МПа , МПа | НВ, HV | HRC | 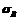 , МПа , МПа |
| 52,4 | 21,2 | ||||
| 57,5 | 22,1 | ||||
| 60,9 | 23,0 | ||||
| 64,1 | 23,9 | ||||
| 67,0 | 24,8 | ||||
| 69,8 | 25,6 | ||||
| 72,4 | 26,4 | ||||
| 74,7 | 27,2 | ||||
| 76,6 | 28,0 | ||||
| 78,3 | 28,8 | ||||
| 79,9 | 29,5 | ||||
| 81,4 | 30,2 | ||||
| 82,8 | 31,6 | ||||
| 84,2 | 33,0 | ||||
| 85,6 | 34,2 | ||||
| 87,0 | 35,3 | ||||
| 88,3 | 36,3 | ||||
| 89,5 | 37,2 | ||||
| 90,6 | 38,1 | ||||
| 91,7 | 38,9 | ||||
| 92,8 | 39,7 | ||||
| 93,8 | 40,5 | ||||
| 94,8 | 41,3 | ||||
| 95,7 | 42,1 | ||||
| 96,6 | 42,9 | ||||
| 97,5 | 43,7 | ||||
| 98,4 | 44,5 | ||||
| 99,2 | 45,3 | ||||
| 46,1 |
Справочные данные общего характера
3.4.1. Множители и приставки для образования десятичных
Кратных и дольных единиц
| Наимено-вание приставки | Обозначение приставки | Множитель | Наименование множителя | |
| рус. | международ. | |||
| эксф | Э | Е | 1000000000000000000 = 1018 | квинтиллион |
| пета | П | Р | 1000000000000000 = 1015 | квадриллион |
| тера | Т | Т | 1000000000000 = 1012 | триллион |
| гига | Г | G | 1000000000 = 109 | миллиард |
| мега | М | М | 1000000 = 106 | миллион |
| кило | к | к | 1000 = 103 | тысяча |
| гекто | г | h | 100 = 102 | сто |
| дека | да | da | 10 = 101 | десять |
| деци | д | d | 0,1 = 10-1 | одна десятая |
| санти | с | с | 0,01 = 10-2 | одна сотая |
| милли | м | m | 0,001 = 10-3 | одна тысячная |
| микро | мк | m | 0,000001 = 10-6 | одна миллионная |
| нано | н | n | 0,000000001 = 10-9 | одна миллиардная |
| пико | п | р | 0,000000000001 = 10-12 | одна триллионная |
| фемто | ф | f | 0,000000000000001 = 10-15 | одна квадриллионная |
| атто | а | a | 0,000000000000000001 = 10-18 | одна квинтиллионная |
В таблице приведены десятичные приставки СИ, обозначающие увеличение (кратные) или уменьшение (дольные) единиц.
Единицы механических величин в международной системе единиц (СИ)
| Величина | Единица СИ | |||
| Наименование | Обозначение | Наименование | Обозначение | Соотношение единиц |
| Сила | F, Q, N | ньютон | Н | 1 Н = 0,102 кгс |
| Напряжение | σ, t | паскаль | Па | 1 Па = 1 Н/м2 |
| Модуль упругости | E, G | паскаль | Па | 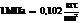 |
| Момент силы | M, T | ньютон-метр | Н·м | 1 Н·м = 0,102 кгс·м |
| Погонная нагрузка | q | ньютон на метр | Н/м | 1 Н/м = 0,102 кгс/м |
Единицы физических и механических величин
Основные единицы
| Длина | L | м |
| Масса | M | кг |
| Время | T | с |
Производные единицы
| Наименование | Сила, вес | Удельный вес | Давление | Плотность | Удельный объём | Момент силы | Работа, энергия | Мощность |
| Размерность | 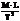 | 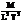 | 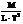 | 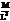 | 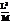 | 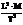 | 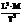 | 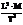 |
| Единицы | Н | 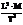 | 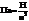 | 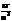 |  | Н·м | Дж = = Н·м | Вт = = Дж/с |
Ньютон – сила, которую следует приложить к массе 1 кг, чтобы сообщить ей ускорение 1 м/с2.
Сила 1 кгс = 9,807 Н.
1 мм ртутного столба (тор) = 133,3 Па.
1 мм водяного столба » 9,81 Па.
10 м водяного столба » 0,0981 Па.
1 атм = 1 кгс/см2 » 0,0981 МПа.
1 бар = 0,1 Н/мм2. 1 бар = 1,0197 атм.
Плотность воды – 999,973 кг/м3 при температуре 3,98 ºС.
Соотношения между единицами давления, напряжения
| Единицы измерения | Бар | Па [Н/м2] | кгс/см2 [атм] | кгс/м2 [мм вод. ст.] | мм рт. ст. |
| 1 Бар | 1∙105 | 1,02 | 10,2∙103 | ||
| 1 Па [Н/м2] | 1∙10-5 | 10,2∙10-5 | 0,102 | 7,5∙10-3 | |
| 1 кгс/см2 [атм] | 0,981 | 98,1∙103 | 1∙104 | 735,6 | |
| 1 кгс/м2 [мм вод. ст.] | 98,1∙10-6 | 9,81 | 1∙10-4 | 73,56 | |
| 1 мм рт. ст. | 1,33∙103 | 133,3 | 13,56∙10-4 | 13,56 |
Соотношения между единицами энергии
| Единицы измерения | кДж | кКал | кг∙м | кВт∙ч |
| 1 кДж | 0,239 | 0,279∙10-3 | ||
| 1 кКал | 4,1868 | 0,00116 | ||
| 1 кг∙м | 0,00981 | 0,00234 | 0,272∙10-5 | |
| 1 кВт∙ч | ||||
| 1 л.с.-час | 2647,8 | 632,3 | 2,7∙105 | 0,736 |
3.4.6. Связь крутящего момента T с мощностью N
и частотой вращения вала n
| Формула момента | Размерность |
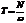 | 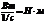 |
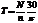 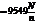 | 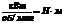 |
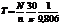  | 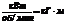 |
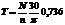 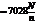 | 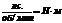 |
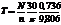  | 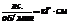 |
Список рекомендуемой литературы
1. Феодосьев, В. И. Сопротивление материалов: учебник для вузов / В. И. Феодосьев. – М.: Изд. МГТУ им. Баумана, 2001. – 592 с.
2. Сопротивление материалов. Конспект лекций. Ч. 1 / В. П. Багмутов [и др.]; ВолгГТУ, Волгоград. 2007. – 128 с.
3. Тимощук, Л. Т. Механические испытания металлов / Л. Т. Тимощук. – М.: Металлургия, 1971. – 224 с.
4. Авдеев, В. А. Техника определения механических свойств материалов / В. А. Авдеев. – М.: Машиностроение, 1965. – 488 с.
5. Степнов, М. Н. Статистические методы обработки результатов механических испытаний: справочник / М. Н. Степнов. – М.: Машиностроение, 1985. – 232 с.
6. Золоторевский, В. С. Механические свойства металлов / В. С. Золоторевский. – М.: Металлургия, 1983. – 350 с.
7. ГОСТ 1497-84. Металлы. Методы испытаний на растяжение. Введ. 01.07.90.
8. ГОСТ 25.503-80. Расчеты и испытания на прочность. Методы механических испытаний металлов. Метод испытания на сжатие. Введ. 01.07.81.
9. Беляев, Н. М. Сопротивление материалов / Н. М. Беляев. – М.: Наука, 1976. – 607 с.
10. Фридман, Я. Б. Механические свойства металлов. Ч. 2. Механические испытания. Конструкционная прочность / Я. Б. Фридман. – 3-е изд. – М.: Машиностроение, 1974. – 368 с.
11. Сопротивление материалов / Г. С. Писаренко [и др.]. – Киев: Вища школа, 1979. – 694 с.
12. Цурпал, И. А. Сопротивление материалов. Лабораторные работы: учеб. пособие для вузов / И. А. Цурпал, Н. П. Барабан, В. М. Швайко. – Киев: Выща школа, 1988. – 255 с.
13. Малинин, Н. Н. Кто есть кто в сопротивлении материалов / Н. Н. Малинин. Под ред. В. Л. Данилова. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2000. – 248 с.
14. Гудков, А. А. Методы измерения твердости металлов и сплавов / А. А. Гудков, Ю. И. Славский. – М.: Металлургия, 1982. – 167 с.
15. Конструкционные материалы: справочник / Б. Н. Арзамасов [и др.]. Под общ. ред. Б. Н. Арзамасова. – М.: Машиностроение, 1990. – 688 с.
16. Справочник. Инженерный журнал № 2. – М.: Машиностроение, 1999. – С. 2–3.
17. Справочник. Инженерный журнал № 1. – М.: Машиностроение, 1999. – С. 2–3.
Вячеслав Петрович Багмутов
Александр Станиславович Столярчук
Валентин Иванович Водопьянов
Олег Викторович Кондратьев
Александр Владимирович Белов
Наталья Георгиевна Неумоина
Анатолий Александрович Поливанов
ОРГАНИЗАЦИЯ И ВЫПОЛНЕНИЕ
ЭКСПЕРИМЕНТАЛЬНО-ТЕОРЕТИЧЕСКИХ
ИССЛЕДОВАНИЙ
В КУРСЕ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Часть 1
Учебное пособие
Редактор Пчелинцева М. А.
Компьютерная верстка Сарафановой Н. М.
Темплан 2010 г., поз. № 7К.
Подписано в печать 23. 12. 2010 г. Формат 60×84 1/16.
Бумага листовая. Печать офсетная.
Усл. печ. л. 8,5. Усл. авт. л. 8,31.
Тираж 500 экз. Заказ №
Волгоградский государственный технический университет
400131, г. Волгоград, пр. Ленина, 28, корп. 1.
Отпечатано в КТИ
403874, г. Камышин, ул. Ленина, 5, каб. 4.5
 |
[1] Вероятно, одними из первых, кто производил испытания материалов на растяжение, были Леонардо да Винчи (1452–1519), Галилео Галилей (1564–1642), Эдме Мариотт (1620–1684), которые исследовали образцы из проволоки, камня, древесины и бумаги.
[2] Запись диаграммы растяжения материала ввёл Жан Виктор Понселе (1788–1867). Он считал диаграмму важнейшей характеристикой материала и отмечал, что площадь, ограниченная этой кривой и осью абсцисс в определённом масштабе, равна отношению работы, необходимой для разрушения образца, к его объёму.
[3] Франтишек Иозеф Герстнер (1756–1832) установил: разгрузка подчиняется закону Гука; при вторичном нагружении пластические деформации возникают при напряжении, от которого производилась разгрузка, т. е. в результате нагружения за пределы пропорциональности границы закона Гука расширяются.
[4] Габриэль Ламе (1795–1870) заметил (1826) образование шейки при испытании образца на растяжение и его нагрев при деформировании за пределом пропорциональности.
[5] Понятия «напряжение» и «деформация» введены Огюстеном Луи Коши (1789–1857) в 1822 г. и Барре Сен-Венаном (1797–1886) в 1845 г.
[6] Введено в практику (1773) Семёном Кирилловичем Котельниковым (1723–1806), академиком Петербургской академии наук, математиком, механиком.
[7] Иоган Баушингер (1834–1893) – немецкий математик, физик, механик. Изобрёл зеркальный тензометр высокой чувствительности, с помощью которого были экспериментально определены модули упругости, коэффициент Пуассона. Он ввёл понятия предела упругости, пропорциональности, текучести.
[8] В России первая машина для испытаний на растяжение была построена в 1824 г. по инициативе Г. Ламе на Петербургском механическом заводе.
[9] Первые машины рычажного типа построены Р. Реомюром (1720) и П. Мушенброком (1729).
[10] Брùнелль или Бринèлль (Brinell) Юхан Август (1849–1925), шведский инженер. Опубликовал труды по металлургии стали и определению твердости металлов и сплавов. Метод определения твердости металлов, названный его именем, он предложил в 1900 г.
[11] Название от английского военно-промышленного концерна «Vickers Limited».
[12] Назван по имени американского металлурга С. П. Рòквелла (S. P. Rockwell).
[13] По имени американского промышленника XX в. А. Шора (A. Shore). Предложен в 1906 г.
[14] Роберт Гук (Нооk), (1635–1703) – английский физик, архитектор, изобретатель, инженер.
[15] Томас Юнг (Young), (1773–1829) – английский физик, медик, астроном, филолог.
[16]Анри Навье (Navier), (1785–1836) – французский инженер, строитель мостов, впоследствии академик.
[17] Симеон Дени Пуассон (Роisson), (1781–1840) – французский физик, механик, математик, астроном.
[18] Шарль Кулон (Coulomb), (1736–1806) – французский математик, астроном, военный инженер, строитель мостов и дорог, академик. Занимался механикой, электричеством, магнетизмом.
[19] Огюстен Луи Коши (Cauchy A. L., 1789–1857) – французский учёный. Опубликовал более 800 работ по математике, механике, физике, астрономии.
[20] Отто Христиан Мор (Mohr O. H., 1835–1918) – немецкий механик и инженер, профессор Высшей технической школы в Дрездене. Круговая диаграмма предложена им в 1882 г.
[21] Продольное волокно – это абстрактное понятие, употребляемое в сопротивлении материалов обычно для обозначения любого элемента бруса, эквидистантного (параллельного) его геометрической оси и имеющего бесконечно малое поперечное сечение площадью dA.
[22] Мгновенной геометрической осью называется направление касательной к криволинейной геометрической оси кривого бруса в рассматриваемом сечении.
[23] Балка – технический термин (брус, работающий на изгиб).
[24] См. раздел «Теория напряженного состояния» в курсе сопротивления материалов (СМ).
[25] См. формулу Дмитрия Ивановича Журавского для касательных напряжений при поперечном изгибе в курсе СМ.
[26] Чистым изгибом называется частный случай изгиба, при котором все внутренние усилия, кроме изгибающих моментов, отсутствуют. При плоском изгибе действует только один момент из двух возможных (см. раздел «Косой изгиб» в курсе СМ).
[27] Применение метода мысленных сечений для определения внутренних усилий см. в курсе СМ.
[28] По гипотезе Сен-Венана (см. раздел «Общие понятия» в курсе СМ), закон распределения напряжений в исследуемых – достаточно удаленных от силовых факторов – сечениях от способа нагружения (роликовая или шариковая опора) не зависит.
[29] Принцип работы мостовой схемы (моста Уитсона) см. в курсе электротехники.
[30] Ввиду малой экспериментальной выборки (небольшого числа опытов), эту погрешность в данном случае можно принять в расширенном интервале ± 10 %.
[31] Существует количественный – более корректный – способ построения графика искомой функции (эмпирической линии регрессии). Для ее нахождения используют метод наименьших квадратов (см. раздел «Регрессионный анализ» в курсе высшей математики).
[32] Дрейф нуля – специальный термин, означающий, что с течением времени показания прибора изменяются, т. е. смещается (дрейфует) от начального положения нуль шкалы. Причины этого явления могут быть различными: нестабильность эксплуатационных характеристик некоторых элементов электронной схемы прибора; изменение температурного режима работы при запуске и пр.
[33] В случае нулевых (или близких к нулю) экспериментальных или расчетных значений напряжений, величины расхождений δ между ними не подсчитываются. В этом случае объем выборки n (см. стр. 92) сокращается.
