Применение регрессионного анализа

Для обработки опытных данных

Для построения эмпирической линии регрессии после визуальной проверки линейности ожидаемой зависимости (см. пункты 2.2.2 и 2.2.3) воспользуйтесь уравнением (2.12). Значения параметров 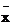, , 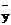, , 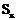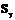r вычислены ранее (см. табл. 2.5). На основании полученных результатов постройте три эмпирические линии регрессии в координатах x, у.

Дисперсию и индивидуальное рассеяние результатов наблюдений вокруг линии регрессии, то есть ошибку определения эмпирической линии регрессии рассчитайте по формулам (2.14), (2.15).

На основании построенных эмпирических линий регрессии установите выборочные (случайные) границы изменения основных параметров прочности (σ_пц , σ_0,2 , σ _в), соответствующие некоторому заданному интервалу допустимых значений твердости (см. раздел 2.1) материала детали. Оцените, с какой ошибкой по напряжению (ошибку привести в МПа) для всех трех исследованных параметров вами установлена каждая из этих границ. Дайте вероятностную трактовку указанных ошибок. Отразите полученные результаты в выводах.

Для расчета и построения на графиках доверительных интервалов расположения теоретических линий регрессии используйте выражения (2.16, 2.17), приведенные в пункте 2.2.2. Уровень значимости α предварительно задается. Результаты расчетов удобно свести в таблицу (рекомендуемая форма приведена в виде табл. 2.6). При расчетах использовать табл. 2.3.

Таблица 2.6

Пример таблицы для оформления результатов регрессионного анализа

(таблица выполняется отдельно для каждой линии регрессии)

Номер	х (твердость)				=	+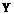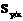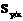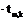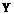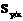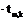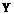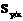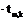
. . .

Границы доверительных областей нанесите пунктирными линиями на графики. Проанализируйте полученные доверительные интервалы для всех трех случаев и отразите результаты такого анализа в своих выводах.

Вопросы для самопроверки

1. Чем обусловлено применение корреляционного и регрессионного методов статистического анализа при обработке результатов механических испытаний элементов конструкций и деталей машин?

2. Сформулируйте основные задачи данного исследования.

3. Что такое объем выборки?

4. Что определяет генеральный коэффициент корреляции; в каких пределах он изменяется?

6. Приведите характерные уровни взаимосвязи между случайными величинами и генеральные коэффициенты корреляции, соответствующие этим уровням.

7. В каких случаях и для чего используют выборочный коэффициент корреляции?

9. При каком условии выборочный коэффициент корреляции стремится к генеральному?

10. Запишите уравнение, связывающее вероятность и уровень значимости.

11. Какой из параметров прочности, по вашим данным, лучше коррелирует с твердостью? Наблюдается прямая или обратная корреляция?

12. Какие зависимости называют уравнением линии регрессии и скедастической зависимостью?

13. Что такое математическая модель линии регрессии?

14. Запишите уравнение и изобразите график эмпирической линии регрессии, принимая линейную гипотезу.

15. Опишите метод линеаризации экспериментальных кривых.

16. Какие задачи решает регрессионный анализ?

17. Как оценить выборочные границы изменения основных параметров прочности, соответствующие заданному интервалу твердости?

18. Расшифруйте понятия теоретической и эмпирической линий регрессии.

19. В каком случае эмпирическая линия регрессии стремится к теоретической?

20. Какая мера используется в качестве ошибки определения эмпирической линии регрессии? Проиллюстрируйте ответ на полученных вами результатах.

21. Какова, по вашему мнению, степень достоверности оценки механических характеристик материала неразрушающими методами контроля (например, по твердости)?

22. Что такое нулевая гипотеза и в чем заключается ее проверка? Покажите на примере собственных расчетов.

23. Запишите формулу преобразования Фишера. Для чего применяется это преобразование?

24. Как, используя распределение Стьюдента, оценить область вероятного расположения теоретической линии регрессии?

25. Сделайте сравнительную оценку доверительных интервалов для изученных прочностных параметров.

26. Что такое выборочные ошибки при определении границ диапазона конкретного параметра прочности?

27. По полученным выборочным результатам дайте вероятностную трактовку параметров прочности исследованного образца (детали).

ПРИЛОЖЕНИЕ

Принятые обозначения

На основе сложившихся в мировой практике традиций стандартом ISO 3898:1997 Bases for design of structures – Notations – General symbols (Основы расчета строительных конструкций. Обозначения. Общие символы) для обозначения отдельных понятий при расчете конструкций предусматривается использование латинских и греческих букв, а также некоторых специальных обозначений, произошедших от терминов на английском, немецком и французском языках. В приведенных ниже таблицах указан преимущественно английский вариант термина. 3.1.1. Латинские прописные буквы
Буква	Значение	От англ. термина
A	Площадь (сечения)	area
D	Диаметр круга, наружный диаметр кольца, жесткость пластин и оболочек при изгибе	diameter
E	Модуль продольной упругости (модуль Юнга)	elasticity
F	Сосредоточенная сила; воздействие вообще	force
G	Постоянная нагрузка (вес); модуль упругости при сдвиге (скольжении)	нем. Gewicht; нем. Gleiten
Н	Горизонтальная составляющая силы; высота (колонны, фермы)	horizontal; height
I	Момент инерции площади сечения	inertia
К	Кинетическая энергия; коэффициент запаса	Kinetic energy; нем. Koeffizient
М	Момент вообще;изгиба­ющий (внутренний) момент	moment
N	Продольное (нормальное к сечению) усилие	normal
Р	Мощность	power
Q	Поперечная сила	нем. Die querlaufende Kraft
R	Опорная реакция; результирующая сила; расчетное сопротивление материала	reaction; resultant; rated resistance
S	Статический момент площади сечения	static moment
Т	Крутящий (внутренний) момент; температура (К)	torsion torque temperature
U	Потенциальная энергия	––
V	Объем тела; верти­кальная составляющая силы	volume; vertical
W	Работа; момент сопротивления сечения	work; нем. Widerstands
X, Y, Z.	Составляющие силы, параллельные осям x, у, z

3.1.2. Латинские строчные буквы
а	Ускорение; расстояние	acceleration
b	Ширина	breadth
d	Внутренний диаметр кольца; диаметр отверстия, болта и т. п.	diameter
е	Эксцентриситет (плечо) силы	eccentricity
f	Стрела прогиба	flexure
g	Ускорение свободного падения	gravity
h	Высота	height
i	Радиус инерции сечения	radius of inertia
k	Коэффициент	нем. Koeffizient
l	Длина элемента; длина пролета	length
m	Масса тела; среднее значение	mass; mean
п	Количество чего-либо	number
р	Давление;интенсивность нагрузки, распределенной по площади	pressure
q	Интенсивность линейной (погонной) распределенной нагрузки	––
r	Радиус	radius
s	Шаг, стандартное отклонение	step, standard deviation
t	Толщина тонкостенных элементов; время; температура (°С)	thickness; time; temperature
u	Удельная потенциальная энергия	––
v	Скорость	velocity
х	Горизонтальная ось поперечного сечения бруса; координата	__
у	Вертикальная ось поперечного сечения бруса и перемещение (прогиб) вдоль нее; координата	––
z	Продольная ось бруса; абсцисса сечения балки	––

3.1.3. Греческие буквы
D	Приращение величины; перемещение
Т	Равнодействующая внутренних касательных сил
α	Угол; коэффициент линейного расширения; отношение диаметров кольца (коэффициент пустотелости)
β	Угол (вообще)
γ	Угол сдвига; угол наклона линии прогиба при косом изгибе; удельный вес материала; коэффициент надежности
d	Перемещение
e	Относительная линейная деформация
θ	Относительное угловое перемещение, поворот
λ,	Гибкость стержня
µ	Коэффициент приведения длины сжатого стержня; отношение предельных напряжений при осевом растяжении и сжатии
n	Коэффициент поперечной деформации (коэффициент Пуассона)
ρ	Радиус кривизны; радиус-вектор; плотность материала
σ	Нормальное напряжение
t	Касательное напряжение
j	Абсолютный угол закручивания; коэффициент продольного изгиба
ω	Площадь эпюры внутренних усилий

3.2. Основные понятия и термины, употребляемые в курсе

Сопротивления материалов

Абсолютная поперечная деформация стержня – разность его поперечных размеров до и после деформации.

Амплитуда– максимальное отклонение от среднего значения .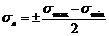

Анизотропи^´я [от греч. ánisos – неравный и tróроs – направление] – зависимость физических свойств вещества (механических, тепловых, электрических, магнитных, оптических) от направления (в противоположность изотропии – независимости свойств от направления).

Асимметричный цикл – цикл, при котором максимальное и минимальное напряжения не равны по абсолютной величине.

База тензометра (торсиометра) – длина участка, на котором производится измерение деформации (расстояние между остриями ножек прибора).

База тензорезистора – длина тензочувствительной части датчика.

Балка[от голл. balk] – конструктивный элемент с прямолинейной геометрической осью, обычно в виде бруса, работающий главным образом на изгиб.

Балка простая–однопролётная балка без консолей, лежащая на двух опорах: шарнирно-подвижной и шарнирно-неподвижной; расстояние между опорами называется пролётом.

Баушингера эффект заключается в понижении сопротивления материала начальным пластическим деформациям (например, предела пропорциональности) при нагружениях, противоположных по знаку предыдущему нагружению.

Безмоментная теория оболочек – теория, согласно которой из шести внутренних усилий отлична от нуля лишь нормальная к сечению сила (мембранная сила), а все моменты и поперечные силы равны нулю.

Бернулли (Bernoulli) – семейство, давшее ряд замечательных людей (семь), преимущественно в области математических наук.

Бернулли гипотеза (гипотеза плоских сечений) – сечения, плоские до деформации, остаются плоскими и в процессе деформации, не поворачиваются, перемещаясь поступательно вдоль оси бруса при растяжении; при изгибе поворачиваются не искривляясь.

Бринелль (Brinell) Юхан Август [1849–1925] – шведский инженер, автор работ по металлургии стали и по определению твёрдости металлов и сплавов. Предложил (1900) статический метод определения твёрдости металлов, получивший широкое распространение в технике.

Брус – тело, одно из измерений которого значительно больше двух других.

Вакансияв кристаллической решётке – узлы, не занятые атомами.

Вал – брус, работающий на кручение. Вращающаяся (обычно в подшипниках) деталь машины, передающая крутящий момент.

Виккерс–британский военно-промышленный концерн.

Внецентренное растяжение(сжатие)–частный случай сложного сопротивления, при которомбрус растягивается силами, параллельными оси бруса так, что их равнодействующая не совпадает с осью бруса, а проходит через точку Р, называемую полюсом силы.

Внешние силы – силы взаимодействия между рассматриваемым элементом конструкции и другими телами, связанными с ним.

Внутренние усилия–силы взаимодействия между частицами тела (кристаллами, молекулами, атомами), стремящиеся сохранить тело как единое целое.

Временное сопротивление(см. «Предел прочности»).

Выносливость – способность материала сопротивляться усталостному разрушению при циклических нагрузках.

Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).

Гибкость стержня– параметр 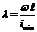, связывающий размеры стержня и способы закрепления его концов при продольном изгибе (см. «Продольный изгиб»).

Гипотеза отсутствия боковых давлений – волокна бруса при изгибе изменяют свою длину, но не давят друг на друга в поперечных направлениях.

Гипотеза плоских сечений (см. «Бернулли гипотеза»). При кручении брусьев некруглого сечения эта гипотеза не справедлива.

Гипотеза постоянства расстояния между сечениями при кручении – расстояния между плоскими поперечными сечениями не изменяются.

Гипотеза прямолинейности радиусов (при кручении) – радиусы, проведённые в плоских поперечных сечениях при кручении, остаются прямолинейными.

Главная плоскость инерции (плоскости)– плоскости, проходящие через главные оси поперечных сечений и геометрическую ось.

Главные деформации– относительные удлинения (ε₁ ≥ ε₂ ≥ ε₃) рёбер параллелепипеда, параллельных главным напряжениям.

Главные моменты инерции– моменты инерции относительно главных осей.

Главные направления– направления, параллельные главным напряжениям.

Главные напряжения – нормальные напряжения, действующие по главным площадкам (то есть площадкам, на которых отсутствуют касательные напряжения).

Главные оси – две взаимно перпендикулярные (ортогональные) оси, относительно которых центробежный момент инерции равен нулю, при этом осевые моменты инерции принимают экстремальные значения (максимальное и минимальное).

Главные площадки – такие, на которых касательные напряжения отсутствуют. Нормальные напряжения, действующие на главных площадках, называются главными.

Гук (Robert Hook) [1635–1722] – английский физик, механик, астроном. Положил начало механике упругих тел, опубликовав в 1678 г. работу, в которой описал установленный им закон пропорциональности между нагрузкой и деформацией при растяжении.

Гука закон – линейные зависимости составляющих напряжений от составляющих деформаций, например, при растяжении – сжатии σ = ε·E, 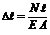; при кручении τ = γ·G, .

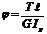Депланация – искривление поперечного сечения бруса, первоначально плоского.

Деформация – изменение формы и размеров тела под действием приложенных сил.

Деформация пластическая – деформация, остающаяся после снятия нагрузки.

Деформация упругая – деформация, исчезающая после снятия нагрузки.

Деформированное состояние в точке – совокупность относительных линейных деформаций и углов сдвига (угловых деформаций) для всевозможных направлений ортогональных осей, проведенных через данную точку.

Динамическая нагрузка – нагрузка, которая сопровождается ускорением частиц рассматриваемого тела или соприкасающихся с ним тел (деталей).

Динамические нагрузки – нагрузки, сопровождающиеся ускорениями как деформированного тела, так и взаимодействующих с ним тел.

Динамический коэффициент – отношение динамического значения некоторого фактора (внутреннего усилия, напряжения, деформации…) к соответствующему статическому значению этого фактора.

Дислокация – область относительного сгущения или разрежения атомов.Дислокации в кристаллах – дефекты кристалла, представляющие собой линии, вблизи которых нарушена характерная для него кристаллическая решетка.

Дифференциальные зависимости при изгибе(см. «Журавского теорема»).

Долговечность – способность конструкции сохранять необходимые для эксплуатации служебные свойства в течение предусмотренного срока (по времени или числу циклов).

Допускаемое напряжение[σ] или σ_adm–определяется по формуле 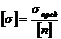. Предельнымиявляются механические характеристики материала, определяемые опытным путём: предел текучести, предел прочности, предел выносливости и др. Нормативный (требуемый) коэффициент запаса прочности [n] регламентируется для строительных конструкций СНиП, для машиностроительных – внутриотраслевыми нормами.

Жёсткость–способность конструктивного элемента воспринимать нагрузки без существенной деформации.

Жёсткость сечения– произведение модуля упругости на геометрическую характеристику поперечного сечения, например, ЕА – при растяжении, GA – при сдвиге, GI_p – при кручении, EI_ос – при изгибе.

Журавский Дмитрий Иванович [1821–1891] – русский учёный и инженер, специалист в области мостостроения и строительной механики.

Журавского теорема– дифференциальные зависимости приизгибе .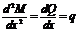

Журавского формула– касательные напряжения в произвольной точке балки при поперечном изгибе .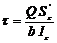

Закон Гука(см. «Гука закон»).

Закон парности касательных напряжений – касательные напряжения по двум ортогональным площадкам; они равны по величине и противоположны по знаку.

Закон сохранения энергии применительно к упругим системам при статическом нагружении – потенциальная энергия внешних сил U_P, действующих на тело, находящееся в равновесии, полностью переходит в потенциальную энергию деформации U этого тела.

Знакопеременный цикл – цикл, при котором максимальное и минимальное напряжения не равны по абсолютной величине и противоположны по знаку.

Знакопостоянный цикл – цикл, при котором максимальное и минимальное напряжения не равны по абсолютной величине и имеют одинаковый знак.

Изгиб– вид деформации, при которой происходит искривление оси прямого бруса или изменение первоначальной кривизны кривого бруса.

Изгиб косой–частный случай сложного сопротивления, при котором силовая плоскость не совпадает с главными плоскостями инерции балки.

Изгиб плоский– случай изгиба бруса, при котором внешние силы лежат в главной плоскости инерции и перпендикулярны к геометрическим осям поперечного сечения. Если сечение имеет ось симметрии, то внешние силы располагаются в плоскости симметрии.

Изгиб плоский поперечный – случай изгиба бруса, при котором внешние силы лежат в главной плоскости и перпендикулярны к геометрическим осям поперечного сечения. Если сечение имеет ось симметрии, то внешние силы располагаются в плоскости симметрии.

Изгиб поперечный – случай изгиба, при котором в поперечных сечениях бруса наряду с внутренним изгибающим моментом М действует и поперечная сила Q.

Изгиб с кручением–частный случай сложного сопротивления, при котором в поперечных сечениях возникают внутренние изгибающий и крутящий моменты.

Изгиб с растяжением–частный случай сложного сопротивления, при котором на брус действуют и продольные, и поперечные нагрузки, пересекающие ось бруса.

Изгиб чистый– вид деформации, при котором из шести внутренних усилий не равны нулю только изгибающие моменты М_z, М_y (либо один из них).

Изгибающий момент – момент, равный сумме моментов внешних сил относительно осей сечения y и z соответственно.

Изотропный материал – материал, свойства которого одинаковы по всем направлениям.

Истинное сопротивление разрыву– напряжение, определяемое отношением нагрузки в момент разрыва к площади поперечного сечения образца в месте разрыва в этот момент S_к = F_к/A_к.

Касательное напряжение – интенсивность внутренних поперечных сил (поперечная сила, приходящаяся на единицу площади в данной точке рассматриваемого сечения).

Консоль– балка с одним защемлённым и другим свободным концом или часть балки, выходящая за шарнирную опору.

Концентраторы напряжений – резкие изменения площади (или формы) поперечного сечения вследствие наличия отверстий, выточек, канавок, надрезов. Приводят к неравномерному распределению напряжений (концентрации напряжений).

Концентра´ция напряже´ний (в упругой области) – сосредоточение больших напряжений на малых участках, прилегающих к местам с резким изменением формы поверхности или сечения деформированного тела.

Коффина зависимость связывает изменение размаха пластической деформации за цикл с числом циклов до разрушения 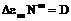,где m и D – постоянные.

Коффина-Мэнсона зависимость 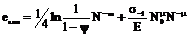связывает амплитуду пластической деформации с числом разрушающих циклов (второй член уравнения определяет упругую составляющую деформации).

Коэффициент концентрации напряженийопределяет кратность повышения наибольших местных напряжений у концентратора по отношению к номинальным в данном сечении.

Коэффициент пустотелости–отношение внутреннего диаметра d трубчатого сечения к наружному D. Обозначают буквой α или с = d/D.

Критерий оптимизации – признак, используемый при оптимизации. Величина, которая в ходе поиска оптимального решения должна принять либо минимум, либо максимум.

Критическая сила– нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы тела.

Критическая температура хрупкости–температура, при которой наблюдается резкое уменьшение ударной вязкости. Обычно это некоторый температурный интервал.

Критическое напряжение – напряжение, соответствующее критической силе при потере устойчивости.

Крутящий момент – момент, равный сумме моментов внешних сил (с одной стороны мысленного сечения) относительно геометрической оси x.

Кручение–вид деформации, при котором из шести внутренних усилий не равно нулю только одно – крутящий момент Т. Кручение возникает при действии на брус внешних сил, образующих момент относительно его геометрической оси.

Кручение с изгибом (см. «Изгиб с кручением»).

Линейное напряжённое состояние ; .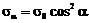

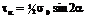Линейно-упругий материал – материал, подчиняющийся закону Гука в виде прямолинейной зависимости.

Мазинга принцип(1926) – кривая повторного нагружения материала совпадает с кривой при первом нагружении, если она построена с изменением знака нагрузки и в масштабе, увеличенном в два раза.

Массив–тело, у которого все три размера одного порядка.

Матрица–таблица расположенных в виде прямоугольника каких-либо математических объектов (чисел, алгебраических выражений…); основное понятие линейной алгебры.

Метод мысленных сечений (РОЗА)применяется для установления связи между внешними нагрузками и внутренними усилиями: Рассечь (мысленно) тело на две части, Отбросить одну из частей, Заменить действие отброшенной части на оставшуюся внутренними усилиями, Анализировать (применить статические уравнения равновесия).

Механические свойства – характеристики материала, описывающие его механическое состояние при внешних силовых воздействиях.

Момент инерции осевой– подсчитанная (интегрированная) по всей площади A сумма произведений элементарных площадок dA на квадраты расстояний от них до этой оси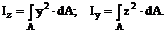

Момент инерции полярный–распространённая на всю площадь A сумма произведений элементарных площадок dA на квадраты расстояний от них до полюса p полярной системы координат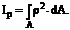

Момент инерции центробежный–распространённая на всю площадь A сумма произведений элементарных площадок dA на расстояния от них до двух ортогональных осей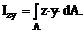

Момент сопротивления–отношение соответствующего момента инерции к расстоянию до наиболее удалённой точки поперечного сечения

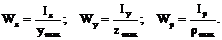
Мор (Mohr) Кристиан Отто [1835–1918] – немецкий учёный в области строительной механики и сопротивления материалов.

Нагрузка распределённая – силы, приложенныенепрерывно на протяжении некоторой длины или площади конструкции. Иначе: поверхностная нагрузка, действующая по узкой площадке большой длины.

Наибольшее местное напряжение – максимальное напряжение, действующее в месте концентрации напряжений.

Наклёп– явление упрочнения материала в результате прохождения пластической деформации; явление повышения предела упругости (текучести) материала вследствие предварительного пластического деформирования (объемного или поверхностного).

Напряжениев точке по сечению – внутренняя сила взаимодействия, приходящаяся на единицу площади у этой точки. Напряжение – величина, характеризующая интенсивность внутренних усилий в точке.

Напряжение касательное τ– напряжение, действующее в плоскости сечения.

Напряжение номинальное– напряжение, вычисленное на основе предположения об отсутствии концентрации напряжений.

Напряжение нормальное σ– напряжение, перпендикулярное к сечению.

Напряжение полное p– напряжение, уравновешивающее внешнюю нагрузку.

Напряжения первого рода(мезонапряжения) – напряжения, величина которых существенно меняется в пределах объёмов, соизмеримых с объёмами кристаллических зёрен или меньших структурных элементов, например, блоков мозаики и пр.

Напряжения первого рода (макронапряжения) – напряжения, уравновешивающиеся в объёмах, значительно превышающих объёмы кристаллических зёрен. Определяются методами теории упругости, теории пластичности или сопротивления материалов на основе континуальной модели среды, не учитывающей структуру реального материала.

Напряжения второго рода (микронапряжения) – напряжения, возникающие в результате нарушения регулярности межатомных связей из-за различных дефектов кристаллической решётки, например, вакансий, дислокаций, дисклинаций и пр. Величина этих напряжений существенно меняется в объёмах на несколько порядков меньших кристаллических зёрен.

Напряжения главные– нормальные напряжения, имеющие экстремальные значения; действуют по главным площадкам. Обозначаются: σ₁ > σ₂ > σ₃.

Напряжённое состояние– совокупность напряжений, действующих по всевозможным ортогональным площадкам, проходящим через рассматриваемую точку.

Нейтральная линия(нейтральная ось НО)– геометрическое место точек, в которых нормальное напряжение в поперечном сечении равно нулю. Иначе: НЛ – след пересечения нейтрального слоя (на котором нормальные напряжения при изгибе равны нулю) с плоскостью поперечного сечения.

Нить– брус с весьма малым по сравнению с длиной поперечным сечением; изгиба не испытывает.

Ньютон–размерность силы. Н –сила, которую следует приложить к массе в 1 кг, чтобы придать ей ускорение 1 м/с² (F = m∙a). 1 Н = 0,102 кгс.

Ньютон(Newton) [1643–1727] – английский физик и математик, создавший теоретические основы механики и астрономии, открывший закон всемирного тяготения, разработавший (наряду с Г. Лейбницем) дифференциальное и интегральное исчисления, изобретатель зеркального телескопа и автор важнейших научных работ по оптике.

Обобщенная сила – это сила или группа сил (с выбранной для расчета силовой размерностью), которую удобно принять при подсчете потенциальной энергии деформации.

Обобщенное перемещение – это тот вид перемещения (линейное, угловое, объемное и т. д.), на котором рассматриваемая обобщенная сила производит работу. Размерность обобщенного перемещения, таким образом, зависит от принятой обобщенной силы.

Оболочка–тело, ограниченное двумя криволинейными поверхностями, у которого длина и ширина велики по сравнению с толщиной.