Правила по технике безопасности и эксплуатации оборудования

1. Запрещается приступать к работе до получения инструктажа по технике безопасности и росписи в журнале.

2. Необходимо помнить, что напряжение в сети – 380 В. Поэтому не следует касаться металлических частей оборудования без необходимости.

3. Перед началом работы надо убедиться в надежности заземления.

4. При создании предварительной нагрузки в 100 Н на приборе Роквелла категорически запрещается переводить малую стрелку индикатора за черный штрих – это влечет за собой поломку прибора.

Лабораторная работа № 4

Упругие свойства металлов. Модули упругости для изотропного тела

Цель работы: экспериментальное определение модуля нормальной упругости, модуля касательной упругости, коэффициента упругой поперечной деформации; проверка справедливости закона Гука, установление связи между постоянными упругости; практическое определение деформаций тензометрическим методом.

Теоретическая часть

Исследуя часовые пружины – этого требовал век, нуждающийся в точных часах для навигации, член Лондонского королевского общества Р. Гук[14] свои заявки на приоритет оговорил в странной работе «Десяток изобретений, которые я намерен опубликовать», вышедшей в 1676 г. Среди других там была «Истинная теория упругости и жёсткости». Под этим заголовком стояла лишь анаграмма ceiiinossttuu, которую можно было понимать как угодно. Лишь двумя годами позже в трактате «De potentia restitutiva» («О восстанавливающей силе») с описанием опы­тов над пружинами и деревянными брусками Гук расшифровал её латинс­кой фразой «Ut tensio sic uis» – «Каково удлинение, такова и сила». Это утверждение известно как закон Гука. Оно является краеугольным камнем всей техники.

Однако при такой формулировке возникает неопределённость: сход­ные кривые «удлинение – сила» можно получить для различных материа­лов, подбирая соответствующим образом форму и размеры тела. Т. Юнг[15] в 1807 г., т. е. по прошествии 130 лет, пришел к выводу, что если абстрагироваться от размеров элемента и вида нагрузки, а пользо­ваться относительным значением деформации и силы (термин «напря­жение» введён А. Навье[16] в 1826 г., т. е. спустя 148 лет после Р. Гука), то закон Гука можно записать в следующем ви­де:

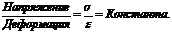
Юнг заключил, что эта константа является неотъемлемой характе­ристикой каждого химического вещества и представляет его жёсткость. Константу упругости назвали модулем Юнга и обозначили Е. Эту константу ещё называют модулем нормальной упругости, или модулем первого рода. Вводя закон Гука, Юнг обращает внимание на то, что этот закон сохраняет силу лишь до известного предела, за которым часть деформации получается не упругой, а составляет её необратимую, остаточную долю.

Описывая опыты на растяжение и сжатие брусьев, Юнг обращает внимание на тот факт, что продольная деформация всегда сопровожда­ется некоторым изменением поперечных размеров. Количественная связь между поперечной и продольной деформациями была исследована Пуассоном[17]. Опыты показали, что коэффициент Пуассона, как и мо­дуль Юнга, отражает особенности атомных взаимодействий, т. е. является отголоском фундаментальных свойств материи.

Деформация изотропного тела в упругой области может быть полностью описана, если известны упругие характеристики данного материала (упругие постоянные): модуль нормальной упругости Е, модуль касательной упругости G и коэффициент поперечной упругой деформации µ.

Модуль нормальной упругости E характеризует сопротив­ляемость мате­риала в упругой области деформации растяжения или сжа­тия. При постоянной температуре модуль нормальной упругости для дан­ного материала как при растяжении, так и при сжатии имеет практически одинаковую величину. Эта упругая характеристика материала входит, на­пример, в формулу закона Гука при растяжении и сжатии для определения абсолютного удлинения (укорочения) Dℓ = ℓ₁ – ℓ (рис. 4.1) или относитель­ной линейной деформации ε = Dℓ /ℓ стержня,

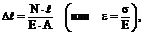(4.1)

где N – внутреннее осевое усилие (σ – нормальное напряжение, σ = N/A);

ℓ – длина стержня или его участка, в пределах которого определяется деформация (начальная длина);

ℓ₁ – длина стержня в деформированном состоянии;

А – площадь поперечного сечения стержня.

Произведение Е·А называется жесткостью сечения при растяженииили сжатии. Если тело испытывает упругопластические деформации, то зависимость между Dℓ и N становится более сложной и закон Гука те­ряет силу. Из формулы (4.1) можно экспериментально определить модуль нормальной упругости E:

(4.2)

определяя деформацию Dℓ (или ε), соответствующую усилию N (или нап­ряжению σ).

Из формулы (4.2) и рис. 4.2 следует геометрический смысл модуля упругости – модуль нормальной упругости соответствует тангенсу угла α наклона начального участка диаграммы растяжения к оси ε.

Рис. 4.1. Схема деформирования стержня при растяжении

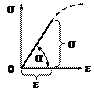
Рис. 4.2. Схема, поясняющая геометрический смысл модуля упругости

Модуль упругости Е имеет размерность напряжения [см. формулу (4.2)], Н/м² = Па, Н/мм² = МПа, из чего следует что модуль упругости – напряжение, которое следует приложить к стержню, чтобы увеличить его длину вдвое (Е = σ при e = 1, т. е. Dℓ = ℓ). Для реальных конструкционных материалов это напряжение примерно в тысячу раз превышает предел упругости. Значения характеристик упругости для ряда конструкционных материалов приведены в приложении.

Коэффициент поперечной упругой деформации µ (коэффициент Пуассона) – упругая постоянная материала. Она устанавливает связь между относительными поперечными 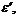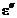и относительной продольной e деформа­циями в упругой области при линейном напряженном состоянии (растя­жении или сжатии) (рис. 4.1).

Относительные деформации стержня соответственно в продольном и поперечных направлениях определяются по формулам:

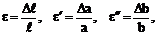(4.3)

где Da = a₁ – a и Db = b₁ – b – абсолютные деформации стержня в поперечных направлениях.

Величину коэффициента Пуассона µ для данного материала определяет отношение поперечной деформации к продольной, взятое по модулю (Da < 0 и Db < 0, т. к. поперечные размеры уменьшаются):

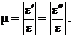(4.4)

Кроме того, величину коэффициента Пуассона можно оценить из из­вестного аналитического соотношения между Е, G, µ:

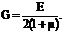(4.5)

Выражение (4.5) показывает, что из трёх постоянных, характеризую­щих упругие свойства изотропного материала, независимыми могут быть только две, так как любую третью можно определить, зная две другие упругие постоянные. Так, из формулы (4.5) следует;

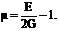(4.6)

Модуль касательной упругости G (модуль сдвига, модуль упругости второго рода) характеризует сопротивляемость материала деформации сдвига в упругой области. Закон Гука при кручении сформулирован в 1784 г. Ш. Кулоном[18]:

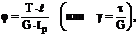(4.7)

где j – угол закручивания (γ – относительный угол сдвига);

Т – крутящий момент, внутреннее усилие (t – касательное напряжение);

I_Р – полярный момент инерции поперечного сечения;

ℓ – длина стержня или участка, в пределах которого определяется деформация.

Крутящий момент и полярный момент инерции в пределах данного участка должны быть постоянными. Произведение G·I_Р называется жест­костью сечения при кручении.

Аналогично растяжению из формулы (4.6) можно вычислить модуль сдвига для материала образца:

(4.8)

Модуль G имеет размерность напряжения Н/м² = Па, Н/мм² = МПа. Напомним, что для круглого сплошного сечения

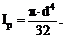
Приборы и оборудование

К настоящему времени разработан ряд экспериментальных методов определения упругих постоянных, из которых можно выделить основные три группы. Это статические, динамические: по скорости распространения упругой волны и по частоте колебаний (Т. Юнг определил величину модуля упругости стали из наблюдения частоты вибраций камертона) – и рентгенографические. Преимущество статических методов определения упругих постоянных заключается в том, что для их реализации не требуется специального оборудования – достаточно штатных испытательных машин и приборов, имеющихся в заводской лаборатории. Статические методы основаны на применении закона Гука при растяжении и кручении. Используется и связь между продольной и поперечной деформациями.

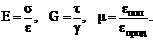
Из приведенных зависимостей следует, что для определения упругих характеристик необходимо измерение линейных и угловых деформаций, т. е. правильно поставленная тензометрия (от лат. tеndо – напрягаю, растягиваю и греч. μετρεω – измеряю). Тензометрия – область техники измерения, занимающаяся определением значения деформации, вызванной механическими напряжениями.

Приборы для измерения деформаций по принципу их действия можно подразделить на механические тензометры (использующие систему рычагов и стрелочных указателей), оптические и электрические. Электри­ческие тензодатчики, в свою очередь, подразделяются на несколько типов, характеризуемых принципом измерения. Индуктивные (перемещение ® изменение индуктивности ® электрический сигнал), ёмкостные (перемещение ® изменение ёмкости ® электрический сигнал), резистивные (от лат. rеsisto – сопротивляюсь, противостою), работающие по принципу: перемещение ® изменение размеров проводника или изменение положения реохорда, или изменение проводимости электролита, или изменение фотосопротивления ® электрический сигнал.

Измерение линейных деформаций при растяжении в настоящей работе осуществляют с помощью резистивных тензодатчиков (тензорезисторов).