Неполная индукция и аналогия.

Неполная индукция – это умозаключение, в котором на основе того, что некоторые объекты класса обладают определенным свойством, делается вывод о том, что этим свойством обладают все объекты данного класса.

Неполная индукция не является дедуктивным умозаключением, поскольку, рассуждая по такой схеме, можно придти к ложному выводу. Следует отметить, что данное умозаключение нельзя считать доказательством, с помощью него можно выдвинуть только гипотезу, которую потом следует доказать или опровергнуть.

Аналогия - это умозаключение, в котором на основании сходства двух объектов в некоторых признаках или наличии у одного из этих объектов еще одного признака делается вывод о том, что второй объект обладает теми же признаками.

Но следует отметить, что не всегда, рассуждая по аналогии, можно получить истинное заключение, а именно перенося переместительное свойство с действия «+» на действие «–» можем получить ложное заключение.

Вывод по аналогии носит характер предположения, гипотезы и поэтому нуждается либо в доказательстве, либо в опровержении.

Построение умозаключения, с помощью которого младшие школьники "открывают" свойство прямоугольника: "В любом прямоугольнике диагонали равны".

Неполная индукция (т.к. все прямоугольники проверить нереально)

Чертим несколько прямоугольников разного размера, потом чертим в них диагонали. Измеряем длину диагоналей в 1 прямоугольнике (равны, потом во втором и третьем,

На основе проведённого эксперимента мы можем предположить, что во всех прямоугольниках диагонали будут равны.

4. Дедуктивные умозаключения. Простейшие схемы дедуктивных умозаключений. Примеры построения дедуктивных умозаключений с использованием этих схем. Построение умозаключения, доказывающего, например, что: «В заданном прямоугольнике противоположные стороны равны».

Дедуктивным называется умозаключение, в котором посылки и заключение находятся в отношении логического следствия.

Если посылки дедуктивного умозаключения обозначить буквами А₁, А₂, …, А_n, а заключение – буквой В, то схематично само умозаключение можно представить так: А₁, А₂, …, А_n → В.

Простейшие схемы дедуктивных умозаключений.

В(х) – общая посылка

А(а) – частная посылка

В(а) - заключение

Примеры построения дедуктивных умозаключений с использованием этих схем.

1. Правило заключения:

# Если запись числа х оканчивается цифрой 5, то число х делится на 5 Запись числа 135 оканчивается цифрой 5. Следовательно число 135 делится на 5.

2. Правило отрицания:

# Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не оканчивается цифрой 5. Следовательно, оно не делится на 5.

3. Правило силлогизма:

# Если число х кратно12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно З.

Построение умозаключения, доказывающего, например, что: «В заданном прямоугольнике противоположные стороны равны».

Для того, чтобы доказать данное утверждение строят общую посылку: если четырехугольник прямоугольный, то его противоположные стороны равны.

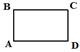
Частная посылка: ABCD – прямоугольник. Заключение: AB=CD, AD=BC

Данное рассуждение проходило по правилу заключения: (А(х) => B(x) и А(ABCD)) => B(ABCD) – верно.

5. Понятие соответствия между множествами. Взаимно однозначные соответствия. Определение числовой функции. Способы задания функций. Примеры числовых функций из начального курса математики, заданных при помощи: а) таблицы; б) выражения с переменной; в) формулы.