Основные проекции, применяемые в навигации: проекция Меркатора, универсальная проекция проекция Меркатора, поперечная равноугольная цилиндрическая проекция.

Картой называют уменьшенное обобщенное изображение земной поверхности на плоскости, выполненное по определенному масштабу и способу.
Так как Земля имеет сферическую форму, ее поверхность невозможно изобразить на плоскости без искажений
Для решения навигационных задач пользуются искаженными, плоскими изображениями земной поверхности — картами.
Все существующие картографические проекции могут быть подразделены на классы по двум признакам: по характеру искажений и по способу построения картографической сетки.

По характеру искажений проекции разделяются на равноугольные, равновеликие и произвольные.
Равноугольные проекции. На этих проекциях углы не искажаются, т. е. углы на местности между какими-либо направлениями равны углам на карте между теми же направлениями.

Равновеликие проекции. На этих проекциях сохраняется пропорциональность площадей фигур

Произвольные проекции. Эти проекции не сохраняют ни подобия фигур, ни равенства площадей, но могут иметь какие-нибудь другие специальные свойства, необходимые для решения на них определенных практических задач.

Цилиндрические проекции. Картографическую нормальную сетку получают путем проектирования координатных линий Земли по какому-либо закону на боковую поверхность касательного цилиндра, ось которого совпадает с осью Земли

Универсальная поперечная проекция Меркатора (UTM)

На глобусе выделено 60 южных и северных зон, каждая шириной 6° по долготе. В каждой зоне есть свой собственный центральный меридиан.

Для картографирования полярных регионов используется система координат Универсальной полярной проекции.

Равновеликая цилиндрическая проекция Берманна

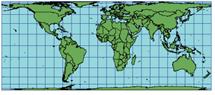Эта равновеликая цилиндрическая проекция подходит для составления карт мира.Цилиндрическая проекция. Стандартные параллели – 30° СШ и 30° ЮШ. Частный случай равновеликой цилиндрической проекции.

Погрешности навигационных измерений, их классификация. Вероятность и частота. Случайные погрешности измерений и их характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.

Погрешности измерений могут быть классифицированы по различным признакам.

По способу выражения их делят на абсолютные и относительные погрешности измерений.

Абсолютная погрешность измерения — погрешность, выраженная в единицах измеряемой величины.

относительная погрешность измерения— отношение абсолютной погрешности измерения к истинному значению измеряемой величины или результату измерений.

По источнику возникновения погрешности измерений делят на инструментальные, методические и субъективные.

Инструментальная погрешность измерения — составляющая погрешности измерения, обусловленная несовершенством применяемого оборудования

Методические погрешности — погрешности, обусловленные несовершенством метода

Субъективная погрешность – это погрешность возникающая из-за низкой степени квалификации оператора средства измерений, а также из-за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.

Ñ Случайной (Сл) погрешностью (СлП) называют погрешность, которая является случайной величиной и может принять в результате опыта то или иное значение, причём заранее неизвестно, какое именно

Среднеквадрати́ческое отклоне́ние (Средняя квадратическая погрешност) – это показатель рассеивания значений случайной величины относительно её математического ожидания.

Математи́ческое ожида́ние — среднее значение случайной величины (распределение вероятностей случайной величины, рассматривается в теории вероятностей)

Дисперсия (от лат. dispersio — рассеяние) в зависимости от контекста может означать:

Диспе́рсия случа́йной величины́ — мера разброса значений случайной величины относительно её математического ожидания.

Закон нормального распределение случайных погрешностей.

Оценка точности измерений.