Глава II. Теория вероятностей. Элементы математической статистики

Глава II. Теория вероятностей. Элементы математической статистики

Теоретические вопросы

1. Основные понятия теории вероятностей.

2. Понятие вероятности события. Классическое определение вероятности события.

3. Элементы комбинаторики.

4. Основные теоремы теории вероятностей.

5. Формула полной вероятности. Формула Байеса.

6. Повторение испытаний. Формула Бернулли. Асимптотические формулы.

7. Дискретные случайные величины. Числовые характеристики ДСВ.

8. Непрерывные случайные величины. Функция распределения, плотность распределения, числовые характеристики НСВ.

9. Нормальное распределение.

10. Элементы математической статистики.

Литература

1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1988.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1979.

Случайные события

Основные понятия теории вероятностей

Испытанием в теории вероятностей называется опыт, при проведении которого задается совокупность условий, не полностью предопределяющих исход этого опыта.

Случайным событием (событием) по отношению к данному испытанию называется явление, которое может произойти или не произойти в зависимости от исхода испытания.

Событие называется достоверным по отношению к данному испытанию, если оно осуществляется при любом исходе данного испытания.

Событие называется невозможным по отношению к данному испытанию, если оно не осуществляется ни при каком исходе данного испытания.

Обозначения событий: A, B, C, … - случайные события; U – достоверное событие , V- невозможное событие.

Два события A и B называются эквивалентными по отношению к данному испытанию, если из осуществления одного из них следует осуществление другого. Обозначение: A=B.

Действия над событиями

Суммой двух событий A и B по отношению к данному испытанию называется событие С, заключающееся в осуществлении хотя бы одного из складываемых событий. Обозначение: С= A+B.

Произведением событий A и B по отношению к данному испытанию называется событие С, заключающееся в одновременном осуществлении обоих перемножаемых событий. Обозначение: С= AB.

Для любых событий A, B и С справедливы следующие свойства действий над событиями:

1) A+B = B+ A

2) A+(B+С)=(A+ B)+С

3) A+ A = A

4) AB= BA

5) A(BС)=(AB)С

6) A A = A

7) AU=A

8) AV=V

9) (A+B)C=AC+BC

Элементы комбинаторики

Конечное множество называется упорядоченным, если его элементы каким-либо образом пронумерованы, т.е. указан порядок следования элементов.

Пусть дано конечное множество M, состоящее из m элементов. Размещением из m элементов по n элементов называется любое упорядоченное подмножество, содержащее n элементов, из множества M, содержащего m элементов. Таким образом, различные размещения отличаются друг от друга либо составом входящих в них элементов, либо порядком их расположения.

Число размещений из m элементов по n элементов обозначается 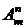и вычисляется по формуле:

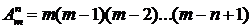(2)

Перестановками из n элементов называются различные упорядочения конечного множества, состоящего из n элементов. Таким образом, различные перестановки отличаются друг от друга лишь порядком элементов. Число перестановок обозначается P_n и вычисляется по формуле:

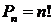(3)

Сочетанием из m элементов по n элементов называется любое подмножество, содержащее n элементов, из множества M, содержащего m элементов. Таким образом, различные сочетания отличаются друг от друга только составом входящих в них элементов.

Число сочетаний из m элементов по n элементов обозначается 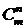и вычисляется по формуле:

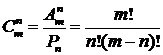(4)

Задание 2. Восемь книг расставлены на полке случайным образом. Найти вероятность того, что две определенные книги окажутся поставленными рядом.

Решение. Воспользуемся классическим определением вероятности события. Общее число элементарных событий в данном случае равно n=P₈=8! - число способов расставить 8 книг на полке (число перестановок из 8 элементов). Событию А благоприятствуют 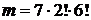элементарных событий (число способов расставить 8 книг так, чтобы 2 определенные книги оказались поставленными рядом). Тогда, согласно классическому определению вероятности события, имеем: .

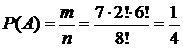Задание 3. На карточках разрезной азбуки напечатаны буквы з, а, д, а, ч, а. Карточки тщательно перемешаны. Найти вероятность того, что на 4-х вынутых по одной и расположенных в ряд карточках, можно будет прочесть слово «дача».

Решение. Общее число элементарных событий в данном случае равно 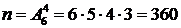- число способов вынуть 4 карточки из имеющихся 6 (число размещений из 6 элементов по 4 элемента). Событию А благоприятствуют 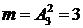элементарных событий (число способов получить слово «дача»). Тогда согласно классическому определению вероятности события имеем: .

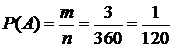Задание 4. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек для участия в соревнованиях. Найти вероятность того, что среди них будет 2 женщины.

Решение. Общее число элементарных событий в данном случае равно 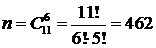- число способов выбрать 6 человек из имеющихся 11 (число сочетаний из 11 элементов по 6 элементов). Событию А благоприятствуют 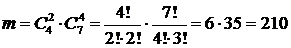элементарных событий (число способов выбрать 6 человек так, чтобы среди них было 2 женщины, а 4 - мужчины). Тогда согласно классическому определению вероятности события имеем: .

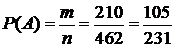Случайные величины

Переменная Х называется случайной величиной по отношению к данному испытанию, если в результате испытания она принимает одно из своих возможных числовых значений, но какое именно, до испытания неизвестно.

Случайные величины принято обозначать большими буквами латинского алфавита, например, X, Y, Z, а их возможные значения - соответствующими малыми буквами – x, y, z.

Функция F(x) действительной переменной x, -∞<x<∞, определяемая формулой

F(x) = P(X<x) ,

называется функцией распределения случайной величины Х.

Свойства функциираспределения:

1) 0≤ F(x) ≤1, -∞<x<∞;

2) F(-∞) =0, F(+∞) =1;

3) F(x) - неубывающая функция на всей оси;

4) F(x) непрерывна слева, т.е. .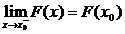

Различают случайные величины дискретного типа (ДСВ) и случайные величины непрерывного типа (НСВ).

Случайная величина Х называется дискретной случайной величиной, если множество ее возможных значений есть числовая последовательность (конечная или бесконечная).

Распределением дискретной случайной величиной называется функция, областью определения которой являются все возможные значения рассматриваемой величины, а областью значений - вероятности соответствующих значений. Распределение ДСВ удобно представлять в виде таблицы:

Возможные значения	x1	x2	x3	….	xn
Вероятности	p1	p2	p3	….	pn

Здесь p_i = P(X=x_i), 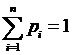(условие нормировки).

Случайная величина Х называется непрерывной случайной величиной, если ее возможные значения заполняют некоторый промежуток (конечный или бесконечный) числовой оси.

Плотностью распределения НСВ Х называется функция f(x), которая определена при всех x, -∞<x<∞, и удовлетворяет условиям:

1) f(x) ≥0 во всей области определения;

2) .

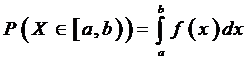Свойства плотности распределения НСВ:

1) Если f(x) -плотность распределения НСВ Х и F(x) – функция распределенияэтойслучайной величины, то

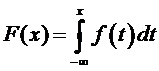
2) Еслиплотность распределения f(x) есть функция непрерывная при 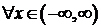, то

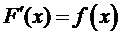
3) 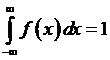(условие нормировки).

Числовые характеристики случайных величин

Математическим ожиданием случайной величины X называется действительное число M(X), определяемое в зависимости от типа случайной величины Х формулой:

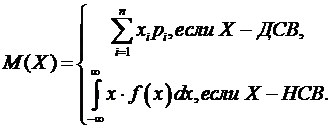
Две случайные величины Х и Y называются независимыми, если для любых x и y имеет место равенство P(X<x, Y<y)= P(X<x) ·P(Y<y).

Свойства математического ожидания:

1) M(C)=C, где C-const;

2) M(CX)=CM(X);

3) M(X±Y)=M(X) ±M(Y), где Х и Y – любые случайные величины;

4) M(X·Y)=M(X) ·M(Y), если Х и Y –независимые случайные величины.

Дисперсией случайной величины Х называется неотрицательное число D(X), определяемое в зависимости от типа случайной величины Х формулой:

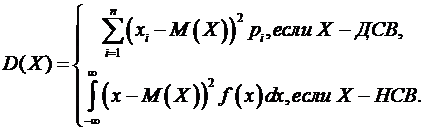
Свойства дисперсии:

1) D(C) =0, где C - const;

2) D(CX)=C² D(X);

3) D(X±Y)=D(X)+D(Y), если Х и Y –независимые случайные величины.

Теорема. Дисперсия любой случайной величины Х равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания:

D(X) = M(X²) - M² (X)

Нормальное распределение

Непрерывная случайная величина Х имеет нормальное распределение с параметрами m, σ (σ >0), если ее плотность определяется формулой:

, .

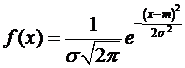Задание 1. Задан закон распределения дискретной случайной величины Х:

xi	-1
pi	0,1	0,2	0,4	0,2	0,1

Найти M(X), M(3X+4), D(X), D(4X- 5).

Решение.

1) По определению математического ожидания:

.

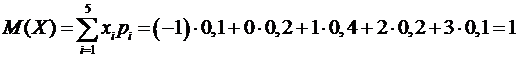2) По свойствам математического ожидания:

.

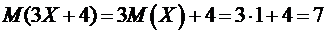3) По теореме о вычислении дисперсии:

.

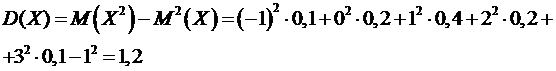4) По свойствам дисперсии:

.

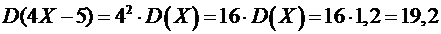Задание 2. Для НСВ Х задана функция распределения:

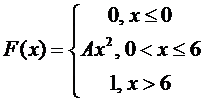
Найти A, f(x), M(X), M(3X-2), D(X), D(2X+4), P(X<5), P(X>1), P(-1<X <3).

Решение.

1) По свойству плотности распределения:

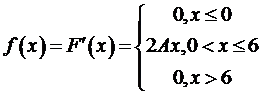
Воспользуемся теперь условием нормировки: 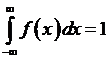. Имеем: 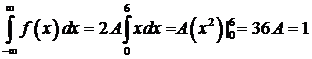, следовательно, .

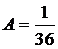2) Тогда плотность распределения случайной величины Х:

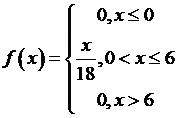
3) По определению математического ожидания:

.

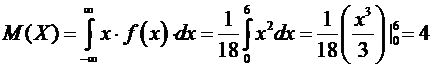4) По свойствам математического ожидания:

.

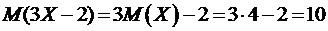5) По теореме о вычислении дисперсии:

.

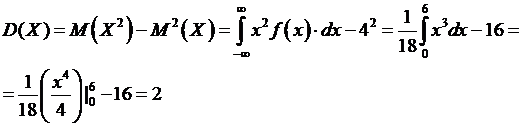6) По свойствам дисперсии:

.

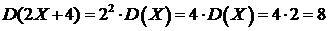7) По определению плотности распределения:

.

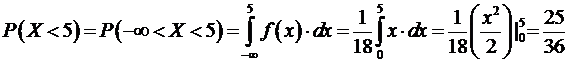8) Аналогично:

.

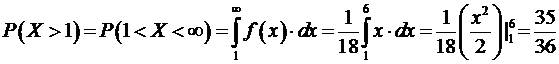9) И, наконец,

.

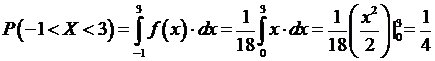Глава II. Теория вероятностей. Элементы математической статистики

Теоретические вопросы

1. Основные понятия теории вероятностей.

2. Понятие вероятности события. Классическое определение вероятности события.

3. Элементы комбинаторики.

4. Основные теоремы теории вероятностей.

5. Формула полной вероятности. Формула Байеса.

6. Повторение испытаний. Формула Бернулли. Асимптотические формулы.

7. Дискретные случайные величины. Числовые характеристики ДСВ.

8. Непрерывные случайные величины. Функция распределения, плотность распределения, числовые характеристики НСВ.

9. Нормальное распределение.

10. Элементы математической статистики.

Литература

1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1988.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1979.

Случайные события

Основные понятия теории вероятностей

Испытанием в теории вероятностей называется опыт, при проведении которого задается совокупность условий, не полностью предопределяющих исход этого опыта.

Случайным событием (событием) по отношению к данному испытанию называется явление, которое может произойти или не произойти в зависимости от исхода испытания.

Событие называется достоверным по отношению к данному испытанию, если оно осуществляется при любом исходе данного испытания.

Событие называется невозможным по отношению к данному испытанию, если оно не осуществляется ни при каком исходе данного испытания.

Обозначения событий: A, B, C, … - случайные события; U – достоверное событие , V- невозможное событие.

Два события A и B называются эквивалентными по отношению к данному испытанию, если из осуществления одного из них следует осуществление другого. Обозначение: A=B.

Действия над событиями

Суммой двух событий A и B по отношению к данному испытанию называется событие С, заключающееся в осуществлении хотя бы одного из складываемых событий. Обозначение: С= A+B.

Произведением событий A и B по отношению к данному испытанию называется событие С, заключающееся в одновременном осуществлении обоих перемножаемых событий. Обозначение: С= AB.

Для любых событий A, B и С справедливы следующие свойства действий над событиями:

1) A+B = B+ A

2) A+(B+С)=(A+ B)+С

3) A+ A = A

4) AB= BA

5) A(BС)=(AB)С

6) A A = A

7) AU=A

8) AV=V

9) (A+B)C=AC+BC