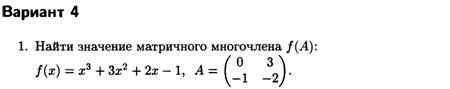Темы 1,2. Матричная алгебра. Определители, обратная матрица
ФОНДЫ ОЦЕНОЧНЫХ СРЕДСТВ
По дисциплине «Линейная алгебра»
Направление подготовки
Экономика»
Квалификация выпускника бакалавр
Форма обучения: очная, заочная
Авторы-составители:
Блохина В.Ф.
кандидат технических наук, старший научный сотрудник, доцент каф. гуманитарных и естественнонаучных дисциплин;
Обсужден и одобрен на заседании кафедры
(протокол №___от « __ » ___ 2017 г)
Москва — 2017
1. Назначение фонда оценочных средств по дисциплине
Цель методических материалов – обеспечить научно-методическую основу для организации и проведения текущего и промежуточного контроля по дисциплине.
Текущий контроль по дисциплине — вид систематической проверки знаний, умений, навыков обучающихся.
Задача текущего контроля — получить первичную информацию о ходе и качестве усвоения учебного материала, а также стимулировать регулярную целенаправленную работу обучающихся.
Промежуточный контроль заключается в объективном выявлении результатов обучения, которые позволяют определить степень соответствия действительных результатов обучения и запланированных в программе. Направлен на проверку конечных результатов обучения, выявление степени усвоения студентами системы знаний, умений и навыков, полученных в результате изучения отдельного предмета.
Задачи промежуточной аттестации — получить полную и достоверную информацию о степени освоения дисциплины.
Формы текущего контроля – практические работы; контрольные работы; тестирование.
Виды контроля:
1 семестр — экзамен
ПАСПОРТ
Фонда оценочных средств
| № | Темы РП (Из РП) | Компетенции по каждой теме | Оценочные средства* | |||
| Тесты | Контрольные работы | Практические занятия | Вопрос и практические задания к зачету и экзамену | |||
| Матричная алгебра | ПК 7, ОПК-2,5, ОК-3 | 1-6 | №1 | Решение задач, предложенных преподавателем | 1-3/1,2 | |
| Определители, обратная матрица. | ПК 7, ОПК-2,5, ОК-3 | 7-11 | №1 | Решение задач, предложенных преподавателем | /3,4 | |
| Линейные пространства | ПК 7, ОПК-2,5, ОК-3 | №2 | Решение задач, предложенных преподавателем | /10,110 | ||
| Векторные линейные пространства, линейные преобразования | ПК 7, ОПК-2,5, ОК-3 | 23, 24 | №2 | Решение задач, предложенных преподавателем | ||
| Ранг матрицы | ПК 7, ОПК-2,5, ОК-3 | 13-15 | №1 | Решение задач, предложенных преподавателем | ||
| Системы линейных уравнений | ПК 7, ОПК-2,5, ОК-3 | 16-21 | №2 | Решение задач, предложенных преподавателем | 7-9 | |
| Задача линейного программирования | ПК 7, ОПК-2,5, ОК-3 | 25, 26 | Решение задач, предложенных преподавателем |
*Оценочные средства:
Средство для оценки текущей аттестации – практические занятия, контрольные работы
Средства для оценки промежуточной аттестации - тесты, вопросы и практические задания к зачету (экзамену).
Перечень оценочных средств
| № | Наименование оценочного средства | Характеристика оценочного средства | Представление оценочного средства в ФОС | Методы оценки результатов |
| Практическое занятие | Средство контроля усвоения учебного материала темы, раздела или разделов дисциплины, организованное как учебное занятие в виде собеседования преподавателя с обучающимися. | Вопросы по темам | экспертный | |
| Тест | Средство, позволяющее оценить уровень знаний обучающегося путем выбора им одного из нескольких вариантов ответов на поставленный вопрос. Возможно использование тестовых вопросов, предусматривающих ввод обучающимся короткого и однозначного ответа на поставленный вопрос. | Тестовые задания | электронный | |
| Контрольные работы | Средство контроля за освоением знаний для решения конкретных задач | Ситуационные задания | экспертный | |
| Вопросы и практические задания к зачету за семестр | Средство контроля, позволяющее проверить уровень освоения тем предмета и навыков решения задач | Вопросы и задания по темам | экспертный |
2. Компетенции, формируемые в результате освоения дисциплины
В результате изучения данной дисциплины студент должен обладать следующими компетенциями:
| ПК 7, ОПК-2,5, ОК-3 | ||
| Этапы формирования компетенции | ||
| Начальный (знает) | Промежуточный (умеет) | Завершающий (владеет) |
| Определение и свойства определителей, обратной матрицы, линейных пространств,векторных линейные пространств, линейных преобразований, ранга матрицы, методы решения систем линейных уравнений однородных и неоднородных. Постановку задач линейного программирования, симплекс-метод, способ решения задач линейного программирования с помощью MS Excel. | Производить арифметические опреации с матрицами, вычислять опеделители и обращать матрицы, определять линейную независимость и зависимость векторов, находить ранг матрицы, определять совместность или несовместность системы, находить ФСР однородной системы, общее решение системы линейных уравнений. Поставить задачу линейного программирования и решить ее с помощью MS Excel. | Методами матричной алгебры, методами решения систем линейных уравнений. Постановкой задач линейного программирования и технологией ее решения с помощью MS Excel |
| Задания для оценивания компетенции на различных этапах её формирования | ||
| Начальный этап — Вопросы 1–46 Промежуточный этап — Задания для самостоятельной работы №1–10, контрольные работы 1¸6, тест 1-66 Завершающий этап —зачет,экзамен. |
Задания для текущего контроля
Практические занятия
| № раздела (темы) дисциплины | Тематика практических занятий | Технологии проведения | Часы | ||
| очное | заочное | очно-заочное | |||
| 1. | Матричная алгебра | Решение задач, предложенных преподавателем | |||
| 2. | Определители, обратная матрица. | Решение задач, предложенных преподавателем. Контрольная работа №5 | |||
| 3. | Линейные пространства | Решение задач, предложенных преподавателем | |||
| 4. | Векторные линейные пространства, линейные преобразования | Решение задач, предложенных преподавателем | |||
| 5. | Ранг матрицы | Решение задач, предложенных преподавателем | |||
| 6. | Системы линейных уравнений | Решение задач, предложенных преподавателем Контрольная работа №6 | |||
| 7. | Задача линейного программирования | Решение задач, предложенных преподавателем |
Контрольные работы
Текущий контроль знаний студентов осуществляется с помощью контрольных работ, выполняемых на практическом занятии по темам 1¸7 и индивидуальных самостоятельных работ, выполняемых дома в ходе подготовки к занятию по «Линейной алгебре». Типовые контрольные работы приведены ниже.
Контрольная работа №1






Контрольная работа №2



5. Найти размерность линейной оболочки векторов (1,-1,3,4,5); (2, 1,3,2,6), (-1,-2,0, 2,-1)

5. Найти размерность линейной оболочки векторов (-1,-2,3,4,5); (2, 1,3,2,6), (3,3,0, -2,1)
Вариант 3

5. Найти базис линейной оболочки векторов (-1,-2,3,4,5); (2, 1,3,2,6), (3,3,0, -2,1)
Вариант 4


5. Найти базис линейной оболочки векторов (5,-2,3,4,5); (2, 1,-3,2,6), (-3,3,-6, -2,1)
Задания для итоговой аттестации
К итоговой аттестации допускается студент, успешно выполнивший контрольные работы и дополнительные задания для самостоятельной работы по всем темам.
Итоговым этапом проверки знаний по данному курсу является экзамен, который проводится в письменной форме. Содержание вопросов одного экзаменационного билета охватывает различные разделы курса с тем, чтобы наиболее более полно отразить пройденный материал. В билет входят:
1. Тестовая часть.
2. Практическая часть.
3. Общетеоретическая часть.
Ниже излагаются основные принципы формирования экзаменационных билетов.
I. Тестовая часть
Перечень тестовых вопросов
1. Если матрицы  и
и  , то матрица 3A – 2B имеет вид
, то матрица 3A – 2B имеет вид
а)  , б)
, б)  , в)
, в)  , г)
, г)  ,д)
,д) 
2. Для матриц  указать те операции, которые можно выполнить:
указать те операции, которые можно выполнить:
а) АВ, б)ВА , в) АТВ, г) ВТА, д) АВТ,е) ВТАТ, ж) АТ ВТ, з) ВАТ
3. При умножении матрицы A на матрицу B справа должно соблюдаться условие
а) число строк матрицы A равно числу строк матрицы B
б) число строк матрицы A равно числу столбцов матрицы B
в) число столбцов матрицы A равно числу столбцов матрицы B
г) если матрицы не квадратные, то они должны быть одинакового размера
д) верный ответ отсутствует
4. Для матриц  элемент c23 произведения С = B A равен:
элемент c23 произведения С = B A равен:
а)1, б)0, в)2, г)-2
5. Квадратная матрица называется диагональной, если
а) элементы, лежащие на побочной диагонали, равны нулю
б) элементы, лежащие на главной диагонали, равны нулю
в) элементы, не лежащие на главной диагонали, равны нулю
г) элементы, лежащие ниже главной диагонали, равны нулю
д) элементы, лежащие на главной диагонали, обязательно равны
6. Квадратная матрица называется верхнетреугольной, если
а) элементы, лежащие на побочной диагонали, равны нулю
б) элементы, лежащие на главной диагонали, равны нулю
в) элементы, не лежащие на главной диагонали, равны нулю
г) элементы, лежащие ниже главной диагонали, равны нулю
д) элементы, лежащие на главной диагонали, обязательно равны
7. При каком a определитель  равен 0
равен 0
а)0 ,б)1 ,в)-1 ,г)1,5
8. При замене некоторой строки невырожденной квадратной матрицы на сумму этой строки и какой-то другой, умноженной на число α, определитель.
а) не изменится
б) поменяет знак
в) умножится на число α
г) станет равным нулю
д) увеличится в два раза
9. Указать верные утверждения, связанные с определением и существованием обратной матрицы:
а) обратная матрица A-1 существует, если матрица A – квадратная и det A ≠ 0
б) обратная матрица A-1 существует, если матрица A – квадратная
в) обратная матрица A-1 существует, если матрица A – квадратная и вырожденная, т.е. det A ≠ 0
г) A·A-1 = A-1·A = E, где E – единичная матрица соответствующего размера
д) A·A-1 = A-1·A = A
е) A·A-1 = A-1·A = 1
10. Элемент  обратной матрицы A– (в случае существования) вычисляется по формуле
обратной матрицы A– (в случае существования) вычисляется по формуле
а) 
б) 
в) 
г) 
д) 
е) 
11. Если матрица  , то элемент
, то элемент  матрицы, обратной к A, равен:
матрицы, обратной к A, равен:
а)4, б)-4 в)1/4 ,г)-1/4 , д)2 , е)-2
12. Чему равен определитель матрицы B, где  .
.
а)4, б)20 в)1 ,г)-1, д)2 , е) 21
13. Указать те преобразования строк (столбцов) матрицы, которые являются элементарными:
а) умножение строки (столбца) на ненулевое число
б) замена элементов строки (столбца) произвольными числами
в) замена строки (столбца) суммой этой строки (столбца) и другой строки (столбца), предварительно умноженной на некоторое число
г) поменять местами две строки (два столбца)
д) замена строки (столбца) нулевой строкой (столбцом)
е) транспонирование матрицы
14. Выбрать верные утверждения. Ранг матрицы равен...
а) числу ненулевых строк в ступенчатом виде матрицы;
б) числу столбцов матрицы;
в) произведению числа строк на число столбцов матрицы;
г) максимальному число линейно независимых строк (столбцов) матрицы;
д) число строк матрицы.
15. Чему равен ранг матрицы 
а)1,б)2,в)3,г)4
е) Ранг матрицы может измениться если
а) транспонировать матрицу,
б) переставить строки,
в) переставить столбцы,
г) умножить строку на ненулевое число,
д) добавить строку
16. Если матрица системы n уравнений квадратная и ее определитель не равен нулю, то система
а) не имеет решений
б) имеет единственное решение
в) имеет не более n решений
г) имеет ровно n решений
д) имеет бесконечно много решений
17. Если  , то
, то
а) 
б) 
в) 
г) 
д) 
18. Число векторов в фундаментальной системе решений однородной системы равно...
а) рангу матрицы системы
б) числу ненулевых строк в ступенчатом виде
в) числу базисных переменных
г) числу свободных переменных
д) наивысшему порядку отличного от нуля минора
е) числу констант в общем решении
19. Чему равно b, при котором система  совместна
совместна
а)1, б)2,в)3,г)4
20. Чему равно значение n, при котором система 
имеет бесконечно много решений.
а)1, б)2,в)3,г)4
21. В системе  базисными можно объявить переменные
базисными можно объявить переменные
а)  ,
,
б) 
в) 
г) 
д) 
е) 
22. В линейном пространстве определены операции:
а) Сложения и умножения на число,
б) Сложения, умножения и умножения на число,
в) Сложения, умножения, деления и умножения на число
23. Набор векторов образует базис линейного векторного пространства если
а) они линейно независимы
б) их количество равно размерности пространства
в) они линейно независимы и любой вектор пространства представим их линейной комбинацией
г) они линейно независимы и их количество равно размерности пространства
д)  они линейно независимы, но добавление к ним еще одного делает их линейно зависимыми
они линейно независимы, но добавление к ним еще одного делает их линейно зависимыми
24. Базисом линейной оболочки векторов являются векторы
а) любые два
б) 
в) 
г) 
д) 
25. Задача, характеризующаяся тем, что целевая функция является инейной функцией переменных, а область допустимых значений определяется системой линейных равенств или неравенств, называется
A. Задача математического программирования
B. Задача линейного программирования
C. Задача динамического программирования
D. Задача о составлении плана производства
26. Последовательное улучшение плана задачи линейного программирования, позволяющее осуществлять переход от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают и за конечное число шагов находится оптимальное решение это
A. Симплекс-метод
B. Стохастическое программирование
C. Смешанные стратегии
D. Семейный спор
II. Практическая часть
Практическая частьвключает в себяоднузадачу прикладного характера, требующую использования знаний по нескольким темам дисциплины, таким как, исследование функций, вычисление площадей фигур и т.п.
Практическая часть экзаменационной работы оценивается от 0 до 2 баллов в зависимости от правильности и полноты решения задачи.
Ниже приводятся примеры заданий практической части экзаменационной работы.
1. Найти  , где
, где 
2. Вычислить  , где
, где  ,
, 
3. Вычислить определитель матрицы 
4. Найти обратную для матрицы 
5. Найти фундаментальную систему решений системы  , где
, где  ,
, 
6. Найти ранг матрицы 
7. Найти решение системы методом Крамера  , где
, где  ,
, 
8. Найти решение системы методом Гаусса.  ,
,  ,
, 
9. Найти ФСР и общее решение системы уравнений
2х1-х2+3х3-2х4+4х5=0
4х1-2х2+5х3+х4+7х5=0
2х1-х2+х3 +8х4+2х5=0
10. Привести пример базиса в R4
11. Найти базис линейной оболочки векторов(3,1,3,4,-2); (-2,1,3,2,6), (-1,-2,0,2,-1), (2,4,6,4,5).
12. Найти матрицу линейного преобразования, переводящего (1,1) в (-3,4) и (0,4) в (5,7).
Вопросы
1. Сколько тонн нефти следует ежедневно перерабатывать в первом режиме?
2. Сколько тонн нефти следует ежедневно перерабатывать во втором режиме?
3. Каков минимальный ежедневный расход нефти?
Задача 4
Металлургическая фирма решает, какое количество чистой стали и какое количествометаллолома следует использовать для приготовления (из соответствующего сплава) литья для одного из своих заказчиков. Литьё поставляется заказчику по цене 9 у.е. за 1 т (1 у.е=$1000). Пусть производственные затраты в расчёте на 1 т чистой стали равняются 3 у.е., а затраты в расчёте на 1 т металлолома – 5 у.е. Последняя цифра больше предыдущей, так как использование металлолома сопряжено с его предварительной очисткой. Заказ предусматривает поставку не менее 5 т литья; при этом заказчик готов купить и большее количество литья, если фирма поставит перед ним такие условия.
Предположим, что запасы чистой стали ограничены и не превышают 4 т, а запасы металлолома не превышают 6 т. Отношение веса металлолома к весу чистой стали в процессе получения сплава не должно превышать 7:8. Производственно-технологические условия таковы, что на процессы плавки и литья не может быть отведено более 18 ч; при этом на 1 т стали уходит 3 ч, а на 1 т металлолома – 2 ч производственного времени.
Вопросы
1. Какое оптимальное количество продукции (литья) следует произвести?
2. Какое оптимальное количество стали и металлолома нужно использовать для выполнения заказа?
3. Изменится ли оптимальный план выпуска продукции, если цена продаваемого литья возрастёт до 10 у.е.?
4. Какое минимальное количество стали может быть использовано для выполнения заказа, если не обращать внимания на оптимизацию прибыли?
Задача5
Фирма «Мелодия» планирует произвести аудиозаписи певицы «Феклы» ипоставить их в города по цене 250 рублей: в город№1 – 500, в город№2 – 300, в город№3 –400, в город№4 – 1000 и в город№4 – 300 кассет. Запись кассет осуществляется на трех студиях, которые могут записать не более определенного количества кассет: студия 1 – 500 кассет, студия 2 – 1000 кассет и студия 3 – 1250 кассет соответственно. Себестоимость одной записи на студии 1 составляет 200 рублей, на студии 2 – 180 рублей, на студии 3 –160 рублей. Транспортные расходы, связанные с доставкой одной кассеты в магазин, составляют в рублях
| город№1 | город№2 | Студия | город№4 | город№5 | |
| Студия1 | |||||
| Студия 2 | |||||
| Студия 3 |
Вопросы
1. Определить максимальную прибыль фирмы.
2. Сколько кассет должна отправить студия 2 в Студия?
3. Какая студия сможет произвести ещё 100 кассет, если возникнет дополнительный спрос?
10. Методические рекомендации по организации изучения дисциплины
Преподавание дисциплины проводится в форме лекций (теоретическая часть курса) и практических занятий в компьютерных классах (компьютерный практикум). В компьютерном классе студенты на каждом занятии работают над выполнением задания по теме под руководством преподавателя. Каждый вид работы, выполняемый студентом, в течение семестра оценивается рейтинговой оценкой.
Для допуска к сдаче зачета студент по каждому виду семестровой работы должен набрать количество баллов не менее зачетного минимума.
| Виды работы | 1 семестр | 2 семестр | ||
| Количество баллов | Количество баллов | |||
| Зачетный минимум | Зачетный максимум | Зачетный минимум | Зачетный максимум | |
| Выполнение практических заданий в течение семестра | ||||
| Контрольная работа | ||||
| Тест | ||||
| Всего | ||||
| Зачет с оценкой | ||||
| Всего по курсу |
Успешность освоения студентом курса «Информационные технологии управления» оценивается по шкале, максимальная сумма баллов которой равняется 100 (ста) баллам. Итоговая оценка семестра является комплексной и выводится на основании результатов зачета и данных о текущей работе студента в учебном процессе.
В течение семестра студент под руководством преподавателя выполняет десять практических заданий. После выполнения практического задания преподаватель проводит опрос по теме занятия.
Критерии оценки практического задания.
| Качество выполнения задания | Оценка по балльной шкале |
| Работа выполнена полностью, без замечаний. На все вопросы даны правильные и точные ответы. | |
| Работа выполнена полностью, с несущественными недочетами. Вопросы раскрыты достаточно полно и правильно. | |
| Работа выполнена с существенными замечаниями. Ответы на вопросы даны в целом правильно, однако неполно. | |
| Работа выполнена не полностью, с существенными замечаниями. Обучающийся не знает до конца ни одного вопроса, путается в основных базовых понятиях. | (работа не засчитана) |
В течение семестра студент выполняет контрольную работу.
Выполнение не менее 90% объема задания контрольной работы без замечаний оценивается в 20—18 баллов.
Выполнение не менее 80 % объема задания контрольной работы (возможно наличие несущественных замечаний оценивается в 17—15 баллов.
Выполнение не менее 60 % объема задания (возможно наличие замечаний оценивается в 14—12 баллов.
Контрольная работа считается успешно выполненной, если студент набрал не менее 12 баллов.
Тестовое задание содержит десять вопросов. Количество набранных по итогам теста баллов соответствует проценту правильных ответов. 100% — 10 баллов. Тест считается пройденным, если студент правильно ответил на 60% вопросов.
ФОНДЫ ОЦЕНОЧНЫХ СРЕДСТВ
По дисциплине «Линейная алгебра»
Направление подготовки
Экономика»
Квалификация выпускника бакалавр
Форма обучения: очная, заочная
Авторы-составители:
Блохина В.Ф.
кандидат технических наук, старший научный сотрудник, доцент каф. гуманитарных и естественнонаучных дисциплин;
Обсужден и одобрен на заседании кафедры
(протокол №___от « __ » ___ 2017 г)
Москва — 2017
1. Назначение фонда оценочных средств по дисциплине
Цель методических материалов – обеспечить научно-методическую основу для организации и проведения текущего и промежуточного контроля по дисциплине.
Текущий контроль по дисциплине — вид систематической проверки знаний, умений, навыков обучающихся.
Задача текущего контроля — получить первичную информацию о ходе и качестве усвоения учебного материала, а также стимулировать регулярную целенаправленную работу обучающихся.
Промежуточный контроль заключается в объективном выявлении результатов обучения, которые позволяют определить степень соответствия действительных результатов обучения и запланированных в программе. Направлен на проверку конечных результатов обучения, выявление степени усвоения студентами системы знаний, умений и навыков, полученных в результате изучения отдельного предмета.
Задачи промежуточной аттестации — получить полную и достоверную информацию о степени освоения дисциплины.
Формы текущего контроля – практические работы; контрольные работы; тестирование.
Виды контроля:
1 семестр — экзамен
ПАСПОРТ
Фонда оценочных средств
| № | Темы РП (Из РП) | Компетенции по каждой теме | Оценочные средства* | |||
| Тесты | Контрольные работы | Практические занятия | Вопрос и практические задания к зачету и экзамену | |||
| Матричная алгебра | ПК 7, ОПК-2,5, ОК-3 | 1-6 | №1 | Решение задач, предложенных преподавателем | 1-3/1,2 | |
| Определители, обратная матрица. | ПК 7, ОПК-2,5, ОК-3 | 7-11 | №1 | Решение задач, предложенных преподавателем | /3,4 | |
| Линейные пространства | ПК 7, ОПК-2,5, ОК-3 | №2 | Решение задач, предложенных преподавателем | /10,110 | ||
| Векторные линейные пространства, линейные преобразования | ПК 7, ОПК-2,5, ОК-3 | 23, 24 | №2 | Решение задач, предложенных преподавателем | ||
| Ранг матрицы | ПК 7, ОПК-2,5, ОК-3 | 13-15 | №1 | Решение задач, предложенных преподавателем | ||
| Системы линейных уравнений | ПК 7, ОПК-2,5, ОК-3 | 16-21 | №2 | Решение задач, предложенных преподавателем | 7-9 | |
| Задача линейного программирования | ПК 7, ОПК-2,5, ОК-3 | 25, 26 | Решение задач, предложенных преподавателем |
*Оценочные средства:
Средство для оценки текущей аттестации – практические занятия, контрольные работы
Средства для оценки промежуточной аттестации - тесты, вопросы и практические задания к зачету (экзамену).
Перечень оценочных средств
| № | Наименование оценочного средства | Характеристика оценочного средства | Представление оценочного средства в ФОС | Методы оценки результатов |
| Практическое занятие | Средство контроля усвоения учебного материала темы, раздела или разделов дисциплины, организованное как учебное занятие в виде собеседования преподавателя с обучающимися. | Вопросы по темам | экспертный | |
| Тест | Средство, позволяющее оценить уровень знаний обучающегося путем выбора им одного из нескольких вариантов ответов на поставленный вопрос. Возможно использование тестовых вопросов, предусматривающих ввод обучающимся короткого и однозначного ответа на поставленный вопрос. | Тестовые задания | электронный | |
| Контрольные работы | Средство контроля за освоением знаний для решения конкретных задач | Ситуационные задания | экспертный | |
| Вопросы и практические задания к зачету за семестр | Средство контроля, позволяющее проверить уровень освоения тем предмета и навыков решения задач | Вопросы и задания по темам | экспертный |
2. Компетенции, формируемые в результате освоения дисциплины
В результате изучения данной дисциплины студент должен обладать следующими компетенциями:
| ПК 7, ОПК-2,5, ОК-3 | ||
| Этапы формирования компетенции | ||
| Начальный (знает) | Промежуточный (умеет) | Завершающий (владеет) |
| Определение и свойства определителей, обратной матрицы, линейных пространств,векторных линейные пространств, линейных преобразований, ранга матрицы, методы решения систем линейных уравнений однородных и неоднородных. Постановку задач линейного программирования, симплекс-метод, способ решения задач линейного программирования с помощью MS Excel. | Производить арифметические опреации с матрицами, вычислять опеделители и обращать матрицы, определять линейную независимость и зависимость векторов, находить ранг матрицы, определять совместность или несовместность системы, находить ФСР однородной системы, общее решение системы линейных уравнений. Поставить задачу линейного программирования и решить ее с помощью MS Excel. | Методами матричной алгебры, методами решения систем линейных уравнений. Постановкой задач линейного программирования и технологией ее решения с помощью MS Excel |
| Задания для оценивания компетенции на различных этапах её формирования | ||
| Начальный этап — Вопросы 1–46 Промежуточный этап — Задания для самостоятельной работы №1–10, контрольные работы 1¸6, тест 1-66 Завершающий этап —зачет,экзамен. |
Задания для текущего контроля
Практические занятия
| № раздела (темы) дисциплины | Тематика практических занятий | Технологии проведения | Часы | ||
| очное | заочное | очно-заочное | |||
| 1. | Матричная алгебра | Решение задач, предложенных преподавателем | |||
| 2. | Определители, обратная матрица. | Решение задач, предложенных преподавателем. Контрольная работа №5 | |||
| 3. | Линейные пространства | Решение задач, предложенных преподавателем | |||
| 4. | Векторные линейные пространства, линейные преобразования | Решение задач, предложенных преподавателем | |||
| 5. | Ранг матрицы | Решение задач, предложенных преподавателем | |||
| 6. | Системы линейных уравнений | Решение задач, предложенных преподавателем Контрольная работа №6 | |||
| 7. | Задача линейного программирования | Решение задач, предложенных преподавателем |
Контрольные работы
Текущий контроль знаний студентов осуществляется с помощью контрольных работ, выполняемых на практическом занятии по темам 1¸7 и индивидуальных самостоятельных работ, выполняемых дома в ходе подготовки к занятию по «Линейной алгебре». Типовые контрольные работы приведены ниже.
Темы 1,2. Матричная алгебра. Определители, обратная матрица
Контрольная работа №1