Выпуклость функции. Точки перегиба.
Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка, то график функции является вогнутым (выпуклым) на этом промежутке.
| Определение. | Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута. |
Если вторая производная дважды дифференцируемой функции при переходе через некоторую точку 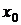 меняет свой знак, то
меняет свой знак, то 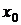 есть точка перегиба ее графика.
есть точка перегиба ее графика.
Схема исследования функции на выпуклость и точки перегиба.
1. Найти ОДЗ функции 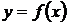 .
.
2. Найти вторую производную функции 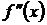 .
.
3. Найти точки, в которых вторая производная 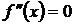 или не существует.
или не существует.
4. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба.
5. Найти значения функции в точках перегиба.
Пример.
Найти интервалы выпуклости и точки перегиба графика функции 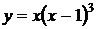 .
.
Решение.
1. ОДЗ: 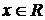 .
.
2. 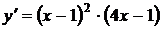 (см. пример №3).
(см. пример №3).
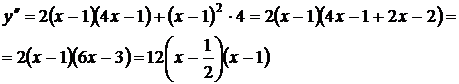 .
.
3. Т.е. 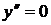 при
при 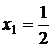 и
и 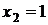 .
.
 |
+ – +
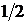 1
1 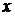
4. 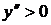 на интервалах
на интервалах 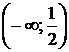 и
и 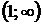 , следовательно, на этих интервалах функция вогнута.
, следовательно, на этих интервалах функция вогнута.
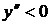 на интервале
на интервале 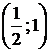 . Следовательно, функция на нем выпукла.
. Следовательно, функция на нем выпукла.
5. 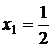 и
и 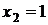 есть точки перегиба.
есть точки перегиба.
Асимптоты графика функции
| Определение. | Асимптотой графика функции 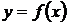 называется прямая, обладающая тем свойством, что расстояние от точки называется прямая, обладающая тем свойством, что расстояние от точки 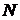 , лежащей на кривой до этой прямой стремится к нулю при неограниченном удалении этой точки графика от начала координат. , лежащей на кривой до этой прямой стремится к нулю при неограниченном удалении этой точки графика от начала координат. |
Различают три вида асимптот: вертикальные, горизонтальные, наклонные.
1. Вертикальные.
Если при 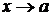
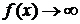 , то
, то 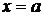 - вертикальная асимптота.
- вертикальная асимптота.
Вертикальные асимптоты следует искать в точках разрыва функции 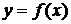 .
.
2. Наклонные.
Прямая 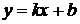 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 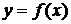 , если существуют конечные пределы:
, если существуют конечные пределы:
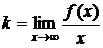 ,
, 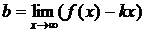 .
.
3. Горизонтальные.
Горизонтальные асимптоты – частный случай наклонных 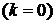 .
.
Пример.
Найти асимптоты кривой 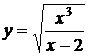 .
.
Решение.
Функция определена в интервалах 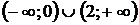 , а
, а 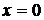 и
и 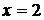 -точки разрыва. Так как
-точки разрыва. Так как 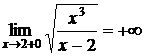 , то прямая
, то прямая 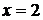 является вертикальной асимптотой кривой;
является вертикальной асимптотой кривой; 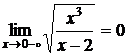 , т.е. прямая
, т.е. прямая 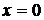 не является вертикальной асимптотой. Горизонтальных асимптот кривая не имеет, так как
не является вертикальной асимптотой. Горизонтальных асимптот кривая не имеет, так как 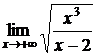 и
и 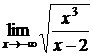 не являются конечными величинами. Определим, существуют ли наклонные асимптоты.
не являются конечными величинами. Определим, существуют ли наклонные асимптоты.
Находим:
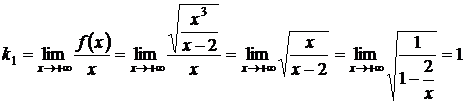 ;
;
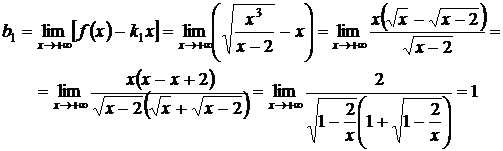 .
.
Таким образом, существует правая наклонная асимптота 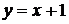 .
.
Аналогично находятся:
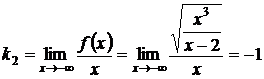 ;
;
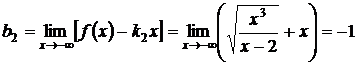 .
.
Итак, существует наклонная асимптота 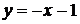 .
.
Общая схема исследования функций и построения их графиков
1. Найти область определения функции и точки разрыва.
2. Исследовать функцию на четность ( 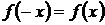 ) – нечетность (
) – нечетность ( 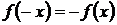 ), периодичность (
), периодичность ( 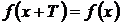 ).
).
3. Найти точки пересечения графика функции с осью 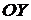 и если это несложно – с осью
и если это несложно – с осью 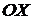 .
.
4. Найти асимптоты кривой.
5. Найти интервалы возрастания и убывания функции и ее экстремумы.
6. Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба.
7. На основе проверенного анализа построить график функции.
Пример.
Исследовать функцию 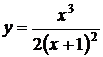 и построить ее график.
и построить ее график.
Решение.
1. Область определения 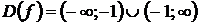 , т.е.
, т.е. 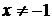 . Точка
. Точка 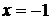 – точка разрыва.
– точка разрыва.
2. Четность, нечетность, периодичность:
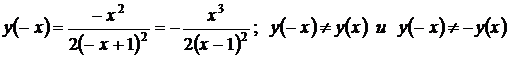 .
.
Значит, функция не является ни четной, ни нечетной; и не является периодичной, т.к. нет такого Т, чтобы выполнилось равенство 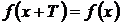 .
.
3. График функции проходит через начало координат.
4. Так как 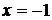 – точка разрыва, найдем предел функции при
– точка разрыва, найдем предел функции при 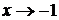 :
:
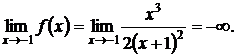
Таким образом, прямая 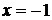 является вертикальной асимптотой.
является вертикальной асимптотой.
Проверим, имеет ли кривая наклонные асимптоты:
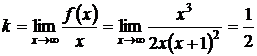 .
.
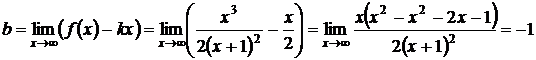 .
.
Т.о., прямая 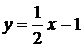 - наклонная асимптота.
- наклонная асимптота.
Горизонтальных асимптот нет.
5. Экстремумы и интервалы монотонности. Найдем:
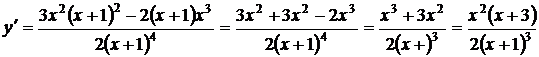 .
.
Производная обращается в ноль, если 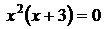 , т.е. при
, т.е. при 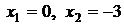 ; производная не существует при
; производная не существует при 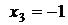 .
.
Однако критическими точками являются только точки 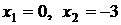 (так как значение
(так как значение 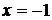 не входит в область определения функции).
не входит в область определения функции).
Поскольку при 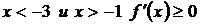 , а при
, а при 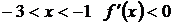 , то
, то 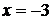 - точка максимума и
- точка максимума и 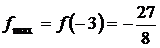 - максимум функции (
- максимум функции ( 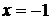 - точка разрыва, т. е. в ней функция не может иметь экстремума).
- точка разрыва, т. е. в ней функция не может иметь экстремума).
На интервале 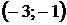 функция убывает, на интервалах
функция убывает, на интервалах 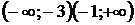 - возрастает.
- возрастает.
6. Интервалы выпуклости и точки перегиба. Найдем:
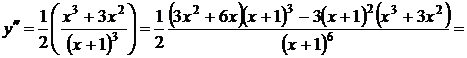
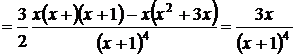 .
.
Вторая производная обращается в ноль при х=0 и не существует при х=-1. Очевидно, что 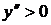 на интервале
на интервале 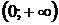 и функция вогнута на этом интервале
и функция вогнута на этом интервале 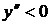 на интервалах
на интервалах 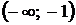 ,
, 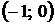 и на этих интервалах функция выпукла. Точкой перегиба является
и на этих интервалах функция выпукла. Точкой перегиба является 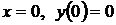 .
.
7. По данным исследований строим график:
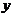 | ||||||||||||||||||||||||
| -3 -1 0 2 | 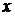 | |||||||||||||||||||||||
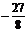 | ||||||||||||||||||||||||
