Что называется моментом инерции твердого тела относительно оси вращения?

Рассмотрим твёрдое тело, которое может вращаться вокруг неподвижной вертикальной оси. Чтобы удержать ось от перемещений в пространстве, заключим её в подшипники. Опирающийся па нижний подшипник фланец Фл , предотвращает передвижение оси в вертикальном направлении .

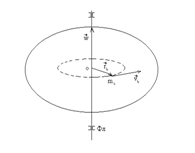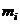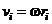Абсолютно твёрдое тело можно рассматривать как систему материальных точек с неизменным расстоянием между ними. Линейная скорость элементарной массы равна , где 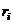-расстояние массы 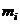от оси вращения. Следовательно, для кинетической энергии элементарной массы получается выражение

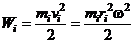
Кинетическая энергия вращающегося твёрдого тела складывается из кинетических энергий его частей.

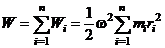
Сумму, входящую в правую часть этого соотношения назовём моментом инерции I тела относительно оси вращения

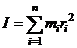- момент инерции твёрдого тела.

27. Получите выражение для момента импульса твердого тела относительно непод­вижной оси вращения.

28. Выведите формулу для момента инерции однородного тонкого стержня длиной / и массы т относительно оси, проходящей через центр масс стержня и перпен­дикулярной стержню.

29. Выведите формулу для момента инерции однородного тонкого стержня дли­ной / и массы т относительно оси, проходящей через конец стержня и перпен-^ \ дикулярной стержню.

30 Выведите формулу для момента инерции однородного тонкого диска радиуса и массы т относительно оси, проходящей через центр масс диска и перпендику лярной плоскости диска.

31. Выведите формулу для момента инерции тонкого обруча радиуса К и массы т относительно оси, проходящей через центр масс обруча и перпендикулярной плоскости обруча.

Пример 1: Вычисление момента инерции тонкого стержня массы m и длинной l, вращающегося вокруг оси перпендикулярной стержню и проходящей через центр масс.

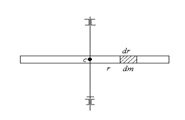Будем считать стержень однородным, тогда

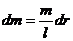
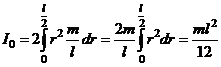
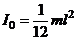
Другие примеры значений моментов инерции для некоторых тел правильной формы приведём без вычислений .

Пример 2:Полый тонкостенный цилиндр, тонкое кольцо :

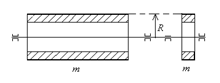
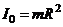- момент инерции цилиндра или

тонкого кольца

Пример 3: Сплошной цилиндр, диск.

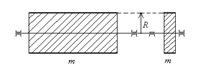
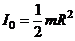- момент инерции сплошного

цилиндра или диска

Пример 4: Сплошной шар .

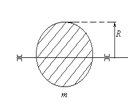
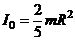- момент инерции шара.

Заметим, что во всех приведённых примерах, тела предполагаются однородными, и вычисляются моменты инерции относительно центральных осей,

т.е. осей проходящих через центр масс.

32. Получите закон сохранения момента импульса твердого тела относительно оси _вращения.

В случае главной оси вращения при суммарном моменте внешней силы, действующем на тело, равном нулю, имеет место закон сохранения момента импульса твёрдого тела: 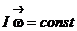- закон сохранения момента импульса твёрдого тела.

Если суммарный момент внешних сил 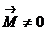, то он совершает работу, которая приводит к увеличению кинетической энергии вращающегося твёрдого тела (в этом случае потенциальная энергия ).

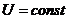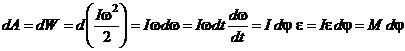
33. Получите формулу кинетической энергии вращающегося твердого тела. Кинетическая энергия(или энергия движения) определяется массами и скоростями рассматриваемых тел. Рассмотрим материальную точку, движущуюся под действием силы 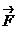. Работа этой силы увеличивает кинетическую энергию материальной точки 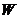. Вычислим в этом случае малое приращение (дифференциал) кинетической энергии:

.

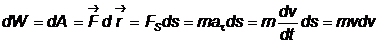При вычислении 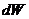использован второй закон Ньютона 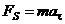, а также 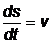- модуль скорости материальной точки. Тогда 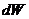можно представить в виде:

-

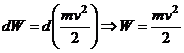- кинетическая энергия движущейся материальной точки.