Дайте определение угловой скорости и углового ускорения вращающегося

Дайте определение угловой скорости и углового ускорения вращающегося

твердого тела и установите их связь с линейными характеристиками точек вра­щающегося тела.

Вращательное движение – это такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Ось вращения может находиться и вне тела.

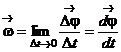- угловая скорость вращающегося тела, где Dt - время, за которое совершается поворот 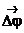. Угловая скорость w измеряется в радианах за 1с. [w] = 1радиан/с = 1с^-1.

Угловая скорость 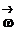направлена вдоль оси, вокруг которой вращается тело, в сторону, определяемую правилом правого винта. Модуль угловой скорости равен .

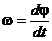Вращение с постоянной угловой скоростью называется равномерным вращением. Если вращение является равномерным, то 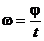, где j - конечный угол поворота за время t. Равномерное вращение можно характеризовать периодом обращения T - временем, в течение которого тело делает один оборот, т.е. поворачивается на угол 2p. Тогда

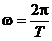,откуда .

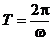Число оборотов единицу времени или частота вращения n равна:

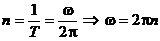- связь угловой скорости с частотой вращения.

Вектор 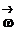может изменяться как за счет изменения скорости вращения тела вокруг оси, так и за счет поворота оси вращения в пространстве. Пусть за время Dt вектор 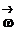получает приращение 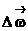. Изменение вектора угловой скорости со временем характеризуется величиной, которая называется угловым ускорением и определяется следующим образом:

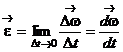- угловое ускорение вращающегося тела.

Угловое ускорение e измеряется в радианах за 1с², т.е. [e] = 1радиан/с² = 1с^-2.

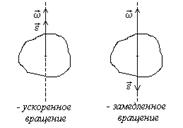Если ось вращения неподвижная, то угловое ускорение направлено вдоль оси вращения. При этом возможны два случая:

В частных случаях равномерного и равнопеременного вращения можно провести аналогию с соответствующими случаями прямолинейного поступательного движения:

Поступательное движение	Вращательное движение
a = 0	e = 0
v =const	w=const
s = vt	j = wt
- - - - - - - - - - -	- - - - - - - - - - -
a = const	e= const
v = v0 + at	w= w0 + et
s = v0t + at2/2	j= w0t + et2/2

Отдельные вращающегося тела имеют различные линейные скорости 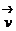. Скорость каждой из точек непрерывно изменяет свое направление. Величина скорости v определяется скоростью вращения тела w и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени Dt тело повернулось на угол Dj. Точка, находящаяся на расстоянии R от оси, проходит при этом путь Ds = RDj. Линейная скорость точки равна

,

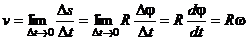т.е. v = wR . ( 1 )

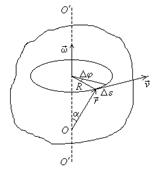
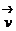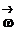Теперь найдем выражение, связывающее векторы и . Положение рассматриваемой точки тела будем определять радиус-вектором 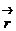. Как видно из рисунка, R = rsina, и формула (1) примет вид

v = wrsina ,

откуда следует

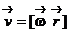- связь между линейной и угловой скоростью для вращающегося твердого тела.

23Что называется моментом силы, действующей на материальную точку, относи­тельно начала координат?

Дайте определение угловой скорости и углового ускорения вращающегося

твердого тела и установите их связь с линейными характеристиками точек вра­щающегося тела.

Вращательное движение – это такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Ось вращения может находиться и вне тела.

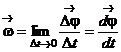- угловая скорость вращающегося тела, где Dt - время, за которое совершается поворот 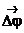. Угловая скорость w измеряется в радианах за 1с. [w] = 1радиан/с = 1с^-1.

Угловая скорость 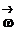направлена вдоль оси, вокруг которой вращается тело, в сторону, определяемую правилом правого винта. Модуль угловой скорости равен .

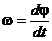Вращение с постоянной угловой скоростью называется равномерным вращением. Если вращение является равномерным, то 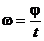, где j - конечный угол поворота за время t. Равномерное вращение можно характеризовать периодом обращения T - временем, в течение которого тело делает один оборот, т.е. поворачивается на угол 2p. Тогда

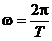,откуда .

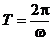Число оборотов единицу времени или частота вращения n равна:

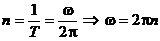- связь угловой скорости с частотой вращения.

Вектор 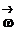может изменяться как за счет изменения скорости вращения тела вокруг оси, так и за счет поворота оси вращения в пространстве. Пусть за время Dt вектор 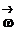получает приращение 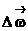. Изменение вектора угловой скорости со временем характеризуется величиной, которая называется угловым ускорением и определяется следующим образом:

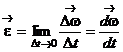- угловое ускорение вращающегося тела.

Угловое ускорение e измеряется в радианах за 1с², т.е. [e] = 1радиан/с² = 1с^-2.

Если ось вращения неподвижная, то угловое ускорение направлено вдоль оси вращения. При этом возможны два случая:

В частных случаях равномерного и равнопеременного вращения можно провести аналогию с соответствующими случаями прямолинейного поступательного движения:

Поступательное движение	Вращательное движение
a = 0	e = 0
v =const	w=const
s = vt	j = wt
- - - - - - - - - - -	- - - - - - - - - - -
a = const	e= const
v = v0 + at	w= w0 + et
s = v0t + at2/2	j= w0t + et2/2

Отдельные вращающегося тела имеют различные линейные скорости 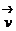. Скорость каждой из точек непрерывно изменяет свое направление. Величина скорости v определяется скоростью вращения тела w и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени Dt тело повернулось на угол Dj. Точка, находящаяся на расстоянии R от оси, проходит при этом путь Ds = RDj. Линейная скорость точки равна

,

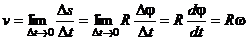т.е. v = wR . ( 1 )

Теперь найдем выражение, связывающее векторы 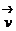и 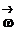. Положение рассматриваемой точки тела будем определять радиус-вектором 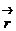. Как видно из рисунка, R = rsina, и формула (1) примет вид

v = wrsina ,

откуда следует

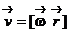- связь между линейной и угловой скоростью для вращающегося твердого тела.

23Что называется моментом силы, действующей на материальную точку, относи­тельно начала координат?