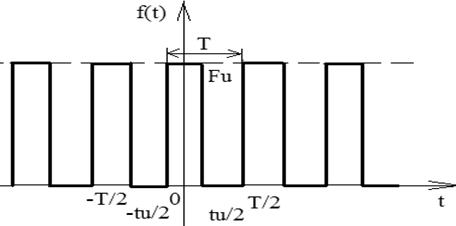
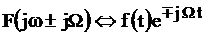Рассмотрим симметричное расположение импульсов

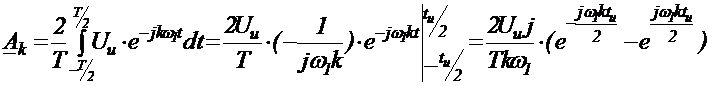
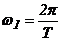
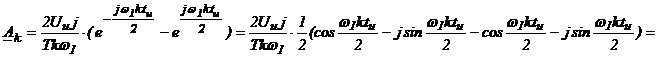
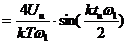
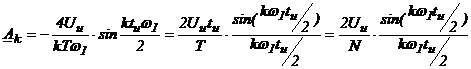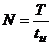, где - скважность.

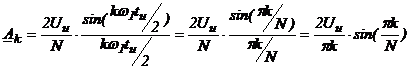
Найдем нулевые точки синуса:

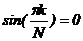
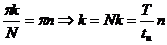
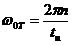Первая нулевая точка – самая важная для спектра последовательности прямоугольных импульсов.

АЧС последовательности прямоугольных импульсов:

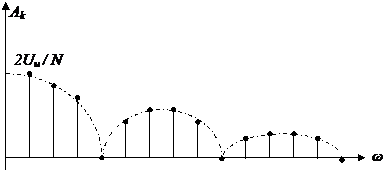
ω₁ ω₂ 2π/t_u 4π/t_u

Основную долю энергии несут гармоники, расположенные от 0 до первой нулевой точки (около 90% энергии). Эту область частот, где сосредоточено 90% энергии сигнала, называют шириной спектра (частотного) сигнала.

Для прямоугольного импульса ширина спектра - .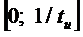

Любая цифровая передача сигнала требует большего спектра, чем простая аналоговая.

ФЧС последовательности прямоугольных импульсов:

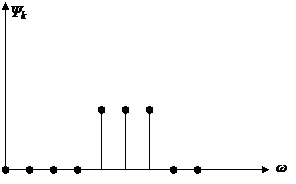если sun(x)>0, то Ψ_k=0

если sin(x)<0, то Ψ_k= π

π

Влияние длительности импульса и периода на вид спектра

Если длительность уменьшается, то основная частота не изменится, нулевые точки переместятся вправо. До первой нулевой точки, где сосредоточена основная энергия, попадает больше составляющих. Технически отмечают, что спектр расширяется.

Если же длительность импульса возрастает, то происходит сужение спектра.

Если период повторения увеличивается, то уменьшается основная частота. Если период повторения уменьшается, то основная частота увеличивается.

Изменение положения импульса или начала отсчета

Это не влияет на АЧС, при этом изменяется только фазовый спектр. Это можно отразить на основе теоремы запаздывания:

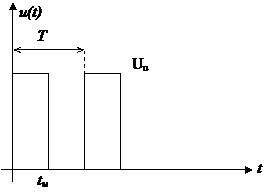
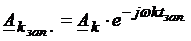
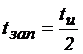
Фазовый спектр смещенного сигнала при N=4:

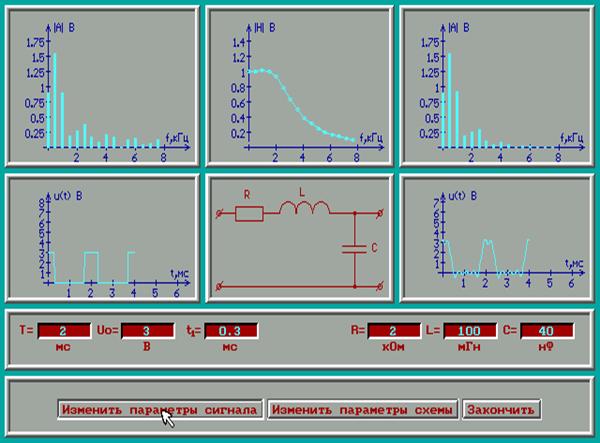
Понятие о расчете цепей при периодических сигналах

Методика расчета:

1. Определяется комплексный спектр периодического сигнала;

2. Оценивается спектр, оставляют наиболее значащие гармоники (первый критерий: отсекаются все, который составляют менее 0,1 от максимальной по величине амплитуды гармоники);

Рассчитываются токи и напряжения от каждой составляющей в отдельности. Можно использовать комплексный метод расчета.

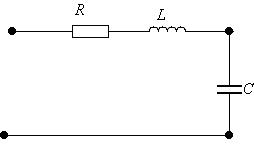
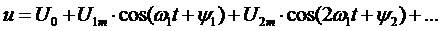
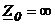I₀=0

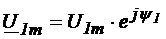
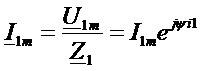
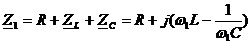
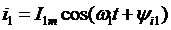
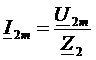
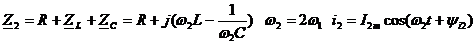
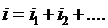
Оценить негармоническую функцию можно по действующему значению, т.е. среднеквадратичному за период:

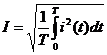
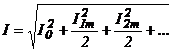
Понятие о спектре непериодического сигнала

Непериодические сигналы являются самыми важными, так как именно они несут информацию. Периодические сигналы являются служебными для передачи информации, а новой информации не несут. Поэтому возникает вопрос спектров непериодических сигналов. Их можно попробовать получить предельным переходом из периодических сигналов, устремив период к бесконечности ( 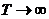). Остается одиночный сигнал. Найдем комплексную амплитуду спектра одиночного сигнала: при .

,

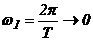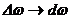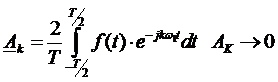
Непериодический сигнал можно разбить на бесконечную сумму гармонических составляющих с бесконечно малыми амплитудами и отличающихся по частоте на бесконечно малые величины – Это называется сплошным спектром не периодического сигнала, а не дискретным. Для расчетов используют понятие не комплексных амплитуд, и комплексной спектральной плотности амплитуд - величины амплитуды, приходящейся на единицу частоты.

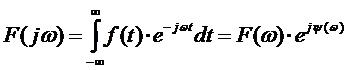Это прямое преобразование Фурье (двухстороннее).

Здесь F(ω) – спектральная плотность амплитуд (модуль), ψ(ω) – спектр начальных фаз (угол).

Размерность плотности амплитуд отличается от размерности исходного сигнала (Вс, В/Гц). Спектр непериодического сигнала похож на спектр такого же по форме периодического сигнала, но является сплошной непрерывной функцией частоты.

Одиночный сигнал можно найти по его спектру обратным преобразованием Фурье.

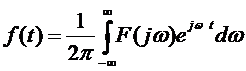
Свойства преобразования Фурье

1. Теорема линейности Если 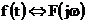, то .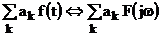

2. Теорема о дифференцировании сигнала по времени. Если 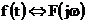, то .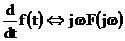

3. Теорема об интегрировании сигнала по времени. Если 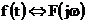, то .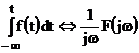

4. Теорема запаздывания ( смещение во времени) Если 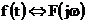, то .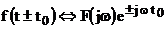

5. Теорема сжатия по времени. Если 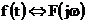, то .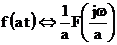

6. Теорема свертки

Если 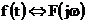, то .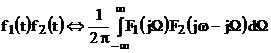

Если 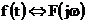, то .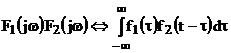

7. Теорема смещения по частоте. Если 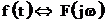, то