А угол – фазо - частотная характеристика (ФЧХ).

АЧХ показывает как изменяется отношение амплитуд выходного и входного сигнала электрической цепи при гармоническом воздействии. Фазо - частотная характеристика (ФЧХ) показывает как изменяется разность фаз выходного и входного сигнала электрической цепи при гармоническом воздействии. (Все это при изменении частоты.) Частотная характеристика показывает частотные свойства электрической цепи.

Методы расчета передаточных функций

При расчете передаточных функций используются законы Ома и Кирхгофа в операторной и комплексной форме обычно при нулевых условиях в зависимости от характеристики. Для сложных цепей приминаются некоторые специальные методы: метод контурных токов, метод узловых напряжений и т.п в операторном виде.

Временные характеристики электрических цепей

Под ними понимают функции времени численно равные реакции электрической цепи на стандартное воздействие на цепь. Применяются обычно для линейных цепей при нулевых условиях (без запаса энергии в цепи).

1. Единичная ступенчатая функция или функция Хевисайда. Определяется следующим способом:

σ(t) =1(t)

σ(t) = 0, t<0

σ(t) = 1, t>0

2. Единичная импульсная функция или функция Дирака.

δ(t)=0, t<0

δ(t)= ¥, t=0

δ(t)=0, t>0

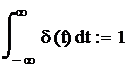
Ее можно рассматривать как предел импульсного сигнала такого вида:

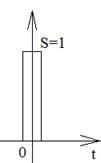t_U=Δt, U_u=1/Δt, Δt→0

В соответствии с испытательными (стандартными) сигналами используются две характеристики:

1. Переходная характеристика - это функция времени, численно равная реакции электрической цепи на единичное ступенчатое воздействие.

h(t) = k(t) = g_σ(t)

Различают в зависимости от типа воздействия и реакции четыре вида переходных характеристик: по напряжению, по току, по сопротивлению и по проводимости.

Размерность переходной характеристики определяется отношением размерности реакции цепи к размерности воздействия.

· по напряжению и по току - безразмерные.

· по сопротивлению - Ом.

· по проводимости - См (сименс).

2. Импульсная характеристика - это функций времени, численно равная реакции электрической цепи на единичное импульсное воздействие.

Обозначается: g_δ(t) = h_δ(t).

Существует также четыре вида импульсных характеристик: по напряжению, по току, по сопротивлению и по проводимости.

Размерность определяется отношением размерностей реакций цепи к размерности площади воздействия. Все импульсные характеристики имеют размерности.

Например, по напряжению - с^-1.

Методики расчета временных характеристик

Переходная характеристика.

· Можно рассчитать классическим методом, подключая ко входу цепи (t=0) источник напряжения (1В) или тока (1А) и рассчитывать ток или напряжение на выходе.

· Можно операторным методом. Аналогично рассчитывать ток или напряжение.

I₂(p) ¸>

U₂(p) ¸> с учетом что на входе U₁(p)= 1/p, потом u₂(t).

· Можно рассчитать через коэффициент передачи.

h (t) ¸ K(p)/p, h(t) = k(t) , U₂(p) = K(p)·U₁(p).

Если найдем оригинал U₂(p) получим переходную характеристику.

· Применяя какие-либо программные средства.

· Экспериментальным путем (по осциллографу).

Импульсная характеристика.

· Классический метод не пригоден, т.к. воздействие бесконечно.

· Операторный метод использовать можно. Здесь изображение воздействия 1.

· Через К(р)

… F₁(p) / F₂(p) = K(p)

g(t) ¸ K(p) Удобно для стандартных цепей.

Программные средства

Через переходную характеристику. Импульсная функция является производной от единичной ступенчатой функции, соответственно и импульсная является производной переходной.

g(t) = h^/(t) + h (0)· δ(t), если h(0) не равна 0.