Вид диаграмм зависит от выбранной частоты по отношению к резонансной.

1) ω<ω₀, U_L < U_C

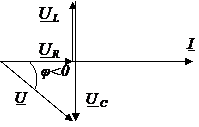
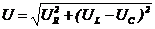
2) ω=ω₀ → U_L=U_C φ=0

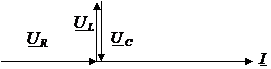
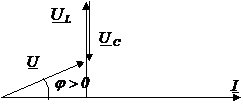3) ω>ω₀. U_L > U_C

Параллельные RLC - цепи

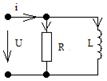
U=I·Z=I/Y 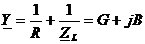Y – комплексная проводимость, B – реактивная Рассмотрим схему с параллельными RLC - элементами:

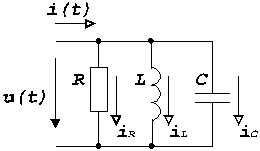
Все ее элементы соединены параллельно и находятся под одним и тем же напряжением u(t)=Um▪sin(wt+y_u). Необходимо определить ток в цепи i(t). На основании 1-го закона Кирхгофа в любой момент времени справедливо соотношение
i(t)=i_R(t)+i_L(t)+i_C(t) .
Отдельные составляющие токов определяются выражениями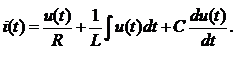
Подставив вместо u(t) гармоническую функцию времени и проведя необходимые математические операции, получим

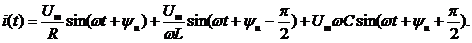
Будем определять искомый ток в виде i(t)=Im▪sin(wt+[K1] y_i).
Перейдем к комплексным мгновенным значениям.

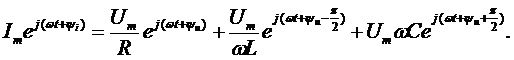
Сокращая на e^jwt и учтя, что 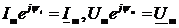, получим

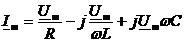
или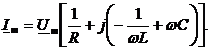
Выражение в скобках – комплексная проводимость цепи Y
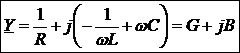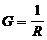, – резистивная составляющая проводимости,
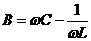– реактивная составляющая проводимости. и она может быть равна 0

на какой-то частоте ω₀, которую называют резонансной.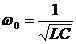

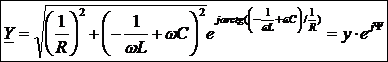
Закон Ома в комплексной форме для цепи записывается
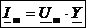или

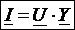
Отсюда следует, что при параллельном соединении ветвей цепи комплексная эквивалентная проводимость равна сумме комплексных проводимостей ветвей:

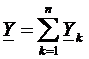Проанализируем векторную диаграмму параллельной RLC - цепи

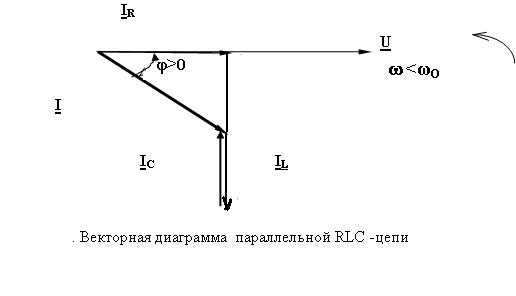
Напряжение взято как опорный вектор, ток в резисторе совпадает по фазе с напряжением , ток в индуктивности отстает на 90⁰, а ток емкостной опережает на 90⁰ и меньше (ω<ω₀). Общий ток равен сумме векторов всех токов и он отстает от напряжения по фазе.

Принцип дуальности в электрических цепях

В электрических цепях есть некоторые понятия, которые с одной стороны противоположны друг другу, а с другой стороны взаимосвязаны и дополняют друг друга (из физики: электромагнитное поле - электрическое поле и магнитное поле). Такие понятия, величины называются дуальными.

У дуальных величин формы записи и математические уравнения одинаковы.

Напряжение ток

Контур узел

Закон Кирхгофа 2 закон Кирхгофа

Сопротивление проводимость

U=I·ZI=U·Y

L C

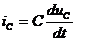
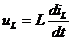
Последовательная цепь параллельная цепь

ИИН ИИТ

Формулы, полученные для некоторой цепи можно формально распространить на дуальные величины в дуальной цепи. Дуальные величины ведут себя одинаково в дуальных цепях, а такие же будут вести себя противоположно в тех же условиях.

Метод токов ветвей (МТВ)

МТВ основан на непосредственном применении законов Кирхгофа к электрической цепи, приводит к решению системы уравнений. Применяется для сложной цепи, особенно если нельзя определить эквивалентное сопротивление цепи или в цепи действует несколько ис­точников.

В качестве основных неизвестных в МТВ используют токи ветвей. В качестве дополни­тельных неизвестных рассматривают напряжения на идеальных источниках тока. Начинают с опре­деления структурных параметров (количество узлов, независимых контуров, ветвей). По первому закону Кирхгофа составляется (N_УЗ-1) уравнений. По второму закону составляется столько уравнений, сколько независимых контуров в цепи N_НК. Причем эти уравнения целесообразно разделить на основные и дополнительные. Поэтому соответ­ственно контуры разделяют на основные и дополнительные. В основные контуры не должны входить идеальные источники тока. Каждый дополнительный контур должен со­держать по одному идеальному источнику тока. Дополнительные уравнения, содержащие напряжения на источниках тока, не включают в систему уравнений, а записывают от­дельно.

Рассмотрим на примере.

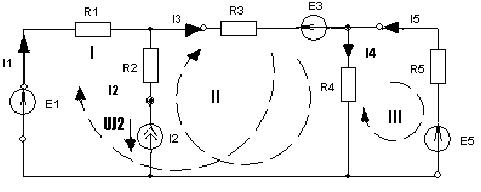
N_уз=3 N_уIзк=2 N_осн.ур.=2

N_нк=3 N_уIIзк=3 N_доп.ур.=1. Число неизвестных токов здесь 4 (I₁, I₃, I₄ ,I₅)