Телекоммуникаций и информатики

Министерство РФ по связи и информатизации

Поволжский Государственный университет

Телекоммуникаций и информатики

Кафедра ТОРС

Конспекты лекций

по дисциплине

для студентов специальности ФО

Самара 2011

ОГЛАВЛЕНИЕ

ОГЛАВЛЕНИЕ.. 2

Общее представление о предмете электротехника. 3

Основные понятия в теоретической электротехнике. 4

Идеальные источники электрической энергии. 5

Понятия об электрической цепи и схеме. 6

Расчет цепей на постоянном токе. 7

Законы Кирхгофа. 8

Переменн ые токи и напряжения. 9

Основные понятия и параметры.. 9

Оценка переменного тока и напряжения. 9

Понятия о комплексных и полных сопротивлениях электрической цепи. 11

Гармонический ток в пассивных элементах электрической цепи. 11

Параллельные RLC - цепи. 16

Принцип дуальности в электрических цепях. 16

. 16

Принцип и метод наложения в теории цепей. 16

Теоремы об эквивалентных источниках или генераторах. 19

(Теорема об автономном двухполюснике) 19

Теорема обратимости или взаимности. 22

Колебательные контуры и. 25

резонансы в электрических цепях. 25

Последовательный колебательный контур. 25

Частотные характеристики последовательного контура. 26

Влияние внешнего сопротивления на избирательность контура. 27

Параллельный колебательный контур (простой) 28

Реальный параллельный контур. 28

Схема замещения: 28

Частотные зависимости параллельного контура. 29

Влияние внешних сопротивлений. 32

на избирательность контура. 32

(Добротность, полоса пропускания, коэффициент подавления) 32

Сложные параллельные контуры.. 33

Расчет мощности в комплексной форме. 36

Баланс мощности в цепях переменного тока. 36

Физический смысл баланса мощности. 37

Определение условия максимума активной мощности. 38

при передаче энергии от источника в нагрузку. 38

Основные понятия о взаимной индукции. 38

Последовательное и параллельное соединения индуктивно. 40

Электрический трансформатор. 41

Входное сопротивление реального трансформатора. 43

Переходные процессы в электрических цепях. 43

Законы коммутации. 44

Начальные и конечные условия. 44

Схемы замещения элементов в различные моменты времени. 45

Классический метод расчета переходных процессов. 45

Анализ переходных процессов в RLC цепях классическим методом.. 46

Последовательные и параллельные RL и RC цепи. 46

Переходные процессы в RLC цепях. 48

Последовательная RLC цепь. 48

Подключение источника постоянного напряжении. 48

Отключение источника в последовательной RLC-цепи. 52

Расчет переходных процессов в сложных цепях. 52

Преобразования Лапласса. 53

Операторные схемы замещения реактивных элементов. 54

Нахождение функции времени в операторном методе. 54

Операторные передаточные функции. 56

Методы расчета передаточных функций. 56

Временные характеристики электрических цепей. 56

Методики расчета временных характеристик. 57

Расчет откликов в электрической цепи на кусочно-непрерывное воздействие. 58

(Интеграллы Дюамеля и наложения) 58

Определение отклика на прямоугольный импульс. 60

Классический метод. 60

Операторный метод. 60

Общие понятия. 62

Дифференцирующие цепи. 62

Интегрирующие цепи. 63

Список литературы

Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. - М.: Гардарики. 1999. –638 с.

Бакалов В.П., Дмитриков В.Ф., Крук Б.И Основы теории цепей. -М.: Радио и связь. 2000, 592 с.

Карлащук В. И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и её применение. - М.: Солон. 1999. –506 с.

Попов В. П. Основы теории цепей. М.: Высшая школа. 2000. –575 с.

Шебес М. Р., Каблукова М. В. Задачник по теории линейных электрических цепей. –М.: Высшая школа. 1990. –544 с.

Бакалов В.П., Крук Б.И., Журавлева О.Б. Теория электрических цепей. Новосибирск. СибГАТИ, 1998, -197 с.

Добротворский И. Н. Теория электрических цепей. Лабораторный практикум. М.: Радио и связь. 1990. –216 с.

Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники. –М.: Радио и связь, 1989. -528 с.

9. Методические указания к лабораторным работам по курсу ТЭЦ “Ис­следо­вание нелинейных цепей с помощью пакета Electronics Workbench”, ка­федра ТЭЦ ПГАТИ. Составители: к.т.н., доц. Михайлов В.И., к.т.н., доц. Алексеев А.П., Самара, 2000.

Основные понятия в теоретической электротехнике

В электротехнике используются понятия

Электрические заряд, ток, напряжение, электрические проводники, диэлектрики или изоляторы, полупроводники, электрическая мощность, излучатели и приемники электромагнитной энергии, источники электрической энергии – в общем, устройства, использующие электрическую энергию, называемые ЭТУ.

· i(t)-электрический ток; I-постоянный ток А

· u(t)-напряжение; U-постоянное напряжение В

· p(t)=u(t)▪i(t)- электрическая мощность ВА

· R-сопротивление (омическое) Ом

· R =0 Ом идеальный проводник

реальный проводник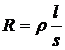

Резистор - деталь ЭТУ, где

Рассмотрим схему цепи

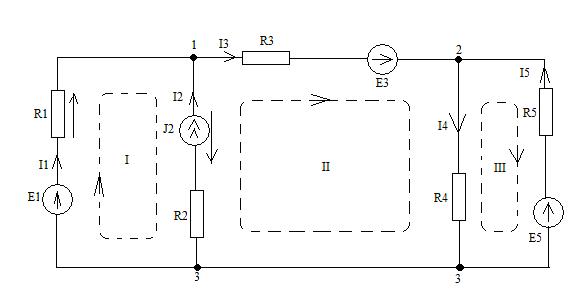
Для проведения расчета сложной цепи используют законы Кирхгофа.

В схеме сложной цепи применяют топологические и структурные понятия и параметры:

· ветвь и количество ветвей;

· узел и их количество;

· контур и их количество.

Ветвь - это участок электрической цепи, где протекает свой, не

разветвляющийся электрический ток. В нашем случае N_В=N_I=5.

Узел - это точка, соединения трех и более ветвей (элементов) электрической цепи. В нашей цепи N_УЗ=3. Узел может быть многоточечным – это когда между точками нет никаких элементов (3 узел).

Контур - это замкнутый путь, проходящий однократно по ветвям и узлам электрической цепи или схемы в явном и неявном виде.

Количество независимых контуров - это такая совокупность контуров, где каждый отличается от других каким-либо элементом. Причем все элементы должны войти в какой-то контур. Для нашей цепи

N_НК=N_В-N_УЗ+1=N_ЗЯ=3

Законы Кирхгофа

Законы Кирхгофа - это физические законы балансов токов в узлах и балансов напряжений в контурах цепи (моделях, схемах замещения).

Первый закон Кирхгофа: Алгебраическая сумма мгновенных значений токов узла равна нулю в любой момент времени.

Правило знаков: токи, направленные к узлу берутся с одним знаком, а от узла с противоположным.

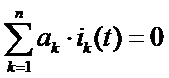, где i_k(t) - мгновенное значение силы тока, а а_k - множитель (-1; 1; 0).

Количество независимых уравнений определяется из условия N_13К(НУ)=N_УЗ -1=2.

Иногда используют другую формулировку первого закона Кирхгофа:

Основные понятия и параметры

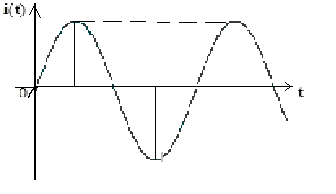Под переменным током или напряжением понимают ток или напряжение, меняющееся периодически по гармоническому закону косинуса или синуса.

i(t)=I_m ·cos(w∙t+j_i),

где I_m – амплитуда тока;

j_i - начальная фаза тока [рад](равна- π/2, так как для косинуса отсчет идет от положительного максимума и по оси с +),

w∙t+j_i – мгновенная фаза в момент времени t.

ω = 2π∙f [рад/с] – угловая частота, f – циклическая частота [Гц]

Т - период колебания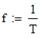

Аналогично для напряжения.

Самое известное действующее значение напряжения 220 В. (311). Обычно стандартные приборы градуируются в действующих значениях. Генераторы тоже градуируют в действующих значениях, но бывает и в амплитудных.

При вращении

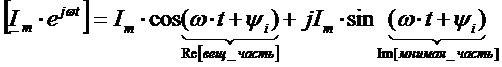
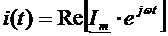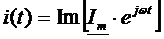(cos) (sin)

Кроме амплитудных комплексных, рассматриваются действующие комплексные значения

.

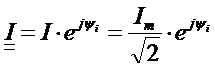Аналогично для напряжения вводятся понятия комплексных амплитудных U_m и действующих значений и U.

Индуктивность.

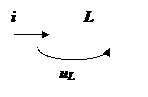
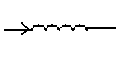
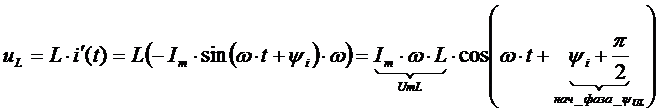
U_mL=I_m∙ωL – амплитуда напряжения на индуктивности пропорциональна частоте,

ωL=x_L - индуктивное сопротивление, φ_L = Ψ_UL-Ψ_i = π/2 - сдвиг фаз между индуктивным напряжением и током (индуктивное напряжение опережает ток на четверть периода (90⁰⁾).

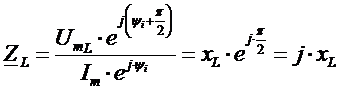- комплексное сопротивление индуктивного элемента, при постоянном токе (ω =0) x_L(0)=0

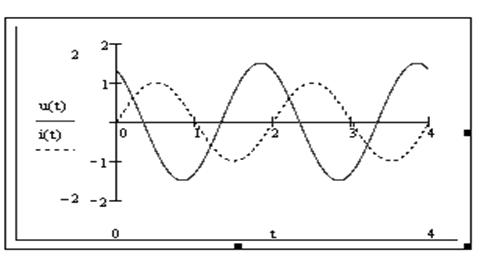
Емкость

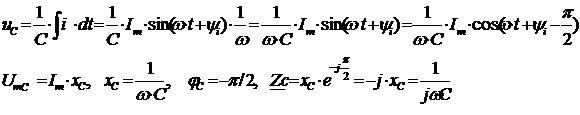
Совокупность нескольких векторов, отображающих токи и напряжения в некоторой цепи, называется векторной диаграммой. Для последовательной RLC – цепи диаграмму строят, откладывая по горизонтали ток, затем также по направлению тока откладывают в масштабе вектор резистивного напряжения, потом из его конца откладывают перпендикулярно вверх вектор индуктивного напряжения и из его конца вниз вектор емкостного.

Параллельные RLC - цепи

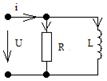
U=I·Z=I/Y 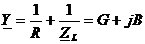Y – комплексная проводимость, B – реактивная Рассмотрим схему с параллельными RLC - элементами:

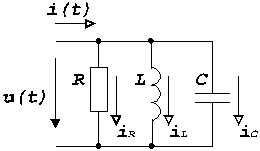
Все ее элементы соединены параллельно и находятся под одним и тем же напряжением u(t)=Um▪sin(wt+y_u). Необходимо определить ток в цепи i(t). На основании 1-го закона Кирхгофа в любой момент времени справедливо соотношение
i(t)=i_R(t)+i_L(t)+i_C(t) .
Отдельные составляющие токов определяются выражениями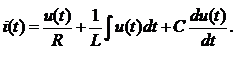
Подставив вместо u(t) гармоническую функцию времени и проведя необходимые математические операции, получим

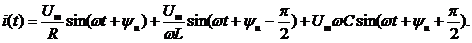
Будем определять искомый ток в виде i(t)=Im▪sin(wt+[K1] y_i).
Перейдем к комплексным мгновенным значениям.

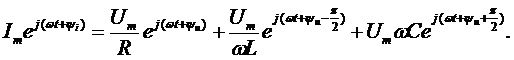
Сокращая на e^jwt и учтя, что 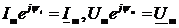, получим

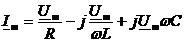
или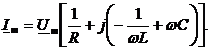
Выражение в скобках – комплексная проводимость цепи Y
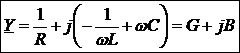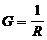, – резистивная составляющая проводимости,
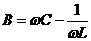– реактивная составляющая проводимости. и она может быть равна 0

на какой-то частоте ω₀, которую называют резонансной.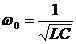

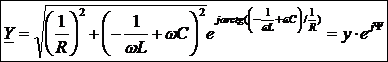
Закон Ома в комплексной форме для цепи записывается
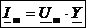или

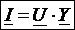
Отсюда следует, что при параллельном соединении ветвей цепи комплексная эквивалентная проводимость равна сумме комплексных проводимостей ветвей:

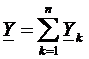Проанализируем векторную диаграмму параллельной RLC - цепи

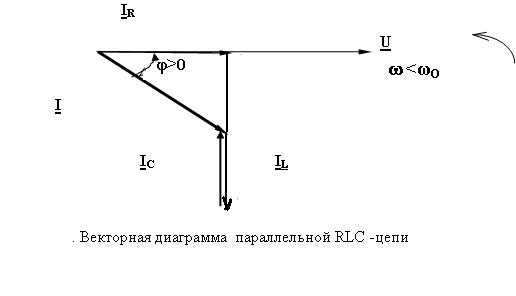
Напряжение взято как опорный вектор, ток в резисторе совпадает по фазе с напряжением , ток в индуктивности отстает на 90⁰, а ток емкостной опережает на 90⁰ и меньше (ω<ω₀). Общий ток равен сумме векторов всех токов и он отстает от напряжения по фазе.

Напряжение ток

Контур узел

Сопротивление проводимость

U=I·ZI=U·Y

L C

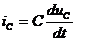
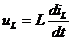
ИИН ИИТ

Формулы, полученные для некоторой цепи можно формально распространить на дуальные величины в дуальной цепи. Дуальные величины ведут себя одинаково в дуальных цепях, а такие же будут вести себя противоположно в тех же условиях.

Метод токов ветвей (МТВ)

МТВ основан на непосредственном применении законов Кирхгофа к электрической цепи, приводит к решению системы уравнений. Применяется для сложной цепи, особенно если нельзя определить эквивалентное сопротивление цепи или в цепи действует несколько ис­точников.

В качестве основных неизвестных в МТВ используют токи ветвей. В качестве дополни­тельных неизвестных рассматривают напряжения на идеальных источниках тока. Начинают с опре­деления структурных параметров (количество узлов, независимых контуров, ветвей). По первому закону Кирхгофа составляется (N_УЗ-1) уравнений. По второму закону составляется столько уравнений, сколько независимых контуров в цепи N_НК. Причем эти уравнения целесообразно разделить на основные и дополнительные. Поэтому соответ­ственно контуры разделяют на основные и дополнительные. В основные контуры не должны входить идеальные источники тока. Каждый дополнительный контур должен со­держать по одному идеальному источнику тока. Дополнительные уравнения, содержащие напряжения на источниках тока, не включают в систему уравнений, а записывают от­дельно.

Рассмотрим на примере.

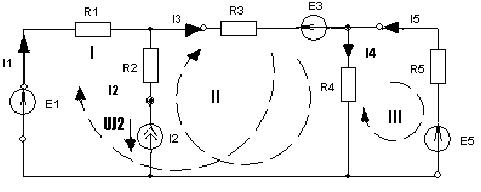
N_уз=3 N_уIзк=2 N_осн.ур.=2

N_нк=3 N_уIIзк=3 N_доп.ур.=1. Число неизвестных токов здесь 4 (I₁, I₃, I₄ ,I₅)

Метод контурных токов

1. Недостатки МТВ

Основной недостаток – довольно большое количество уравнений и соответственно трудоемкость работы.

Поэтому были разработаны другие методы, в частности метод контурных токов (МКТ) и метод узловых напряжений или потенциалов (МУН), где меньше уравнений.

2. Основы МКТ

В качестве неизвестных здесь используются так называемые контурные токи. Это некоторые условные мысленные токи, протекающие по выбранным независимым контурам. В качестве дополнительных неизвестных берутся напряжения на идеальных источниках тока. Система уравнений составляется только на основе второго закона Кирхгофа с применением закона Ома. Конкретные токи ветвей (действительные токи) определяются как алгебраическая сумма соответствующих контурных токов, протекающих через ветвь.

3. Определение числа уравнений и выбор контуров для МКТ

Количество уравнений определяется по формуле:

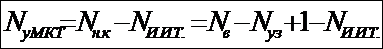
Контуры выбираются так, чтобы в них не входили идеальные источники тока (основные контуры). Дополнительные контуры выбираются с одним источником тока. Их уравнения в систему не включаются, но их влияние учитывается при решении системы.

4. Пример использования

I1

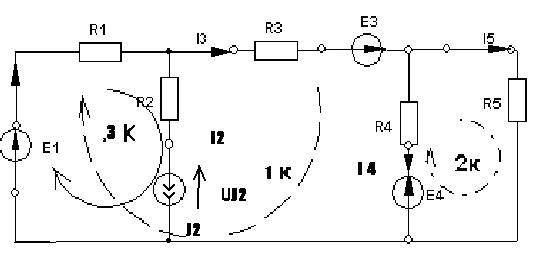
N_B=5, N_УЗ=3, N_ИИТ=1.

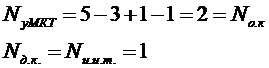Выбираем 1 и 2 контуры без идеальных источников тока. Составляем систему уравнений для основных контуров (1 и 2), используя контурные токи I_1К,I_2К, причем I_3К=J₂..

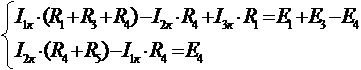
Решив данную систему и определив контурные токи, найдем токи ветвей следующим образом:

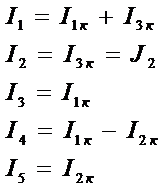
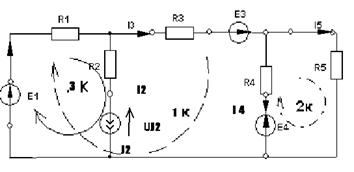
Для определения напряжения на источнике тока составляется вспомогательное уравнение по закону Кирхгофа для дополнительного (3) контура: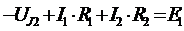

Можно выделить алгоритм расчета:

Решение системы уравнений

Определение токов ветвей

Пример 1

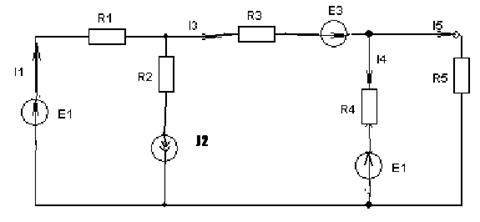
В данном случае мы можем использовать только метод наложения. Составим две схемы замещения, в первой из которых рассчитываются частичные токи от источника постоянной эдс. Поэтому в ней индуктивность заменена перемычкой, а емкость – разрывом. Во второй схеме рассчитываются частичные токи от источника переменного тока и здесь необходимо перевести все токи, напряжения и сопротивления в комплексную форму и записать законы Кирхгофа в комплексной форме.

I1E1 IR2E1 C i1 j2 iR2 j2 ic j2 L I3E1 i2 = j2 i3 j2

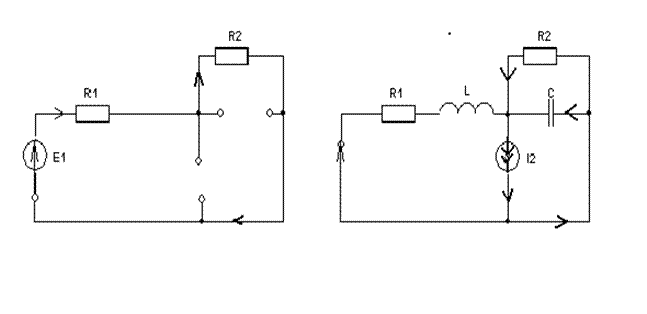
I_1E1=E1/(R1+R2)=I_2E1=I_3E1. Тут надо составлять уравнения по МКТ в комплексной форме. Например, по 1 закону

I_1J2+ I_R2J2+ I_CJ2 –J₂=0, - I_CJ2 - I_R2J2+ I_3J2=0.

Можно использовать и общую проводимость относительно источника тока. 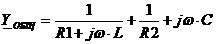, , 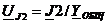, 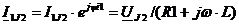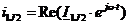. Аналогично остальные токи

В итоге получается, что i₁=I_1E1+i_{1 j2}, i_R2=I_R2E1 – i_R2j2, ic=i_cj2,

i₃=I_3E1 – i_3j2, i₂=j₂.

Доказательство

Применим метод контурных токов, будем выбирать контуры так, чтобы первая ветвь входила только в один первый контур, а вторая – только во второй контур, тогда токи этих ветвей будут равны этим контурным токам.

В первой схеме:

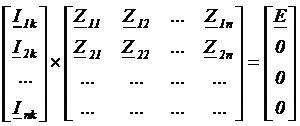Здесь Z_11,22…nn.-контурные сопротивления, Z_12,13,….ki – взаимные сопротивления контуров.

Во второй :

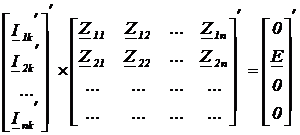, тогда

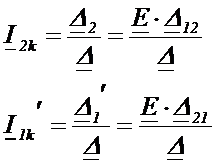
Эти два выражения отличаются на 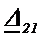и 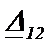. Если все элементы в цепи обратимы, то 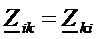. В этом случае 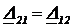и .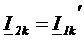

Применение теоремы

Теорему целесообразно применять при расчете токов методом наложения, когда надо находить частичные токи от каждого источника в отдельности, рассчитав ток от одного источника напряжения и пропорционально изменяя токи от источников в других ветвях.

Примеры

Теорему взаимности целесообразно применять в методе наложения, когда ищутся частичные токи от отдельных источников. Найдя ток от одной ЕДС во всех ветвях можно сразу сказать, что другие ЕДС вызовут в этой ветви токи пропорциональные их отношению.

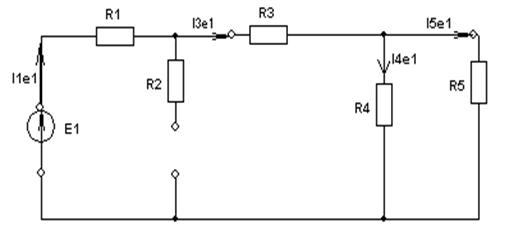
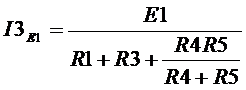, тогда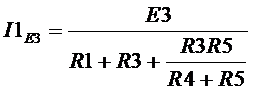

Колебательные контуры и

В зависимости от вида реакции и воздействия различают четыре типа передаточных функций: по напряжению (напряжение / напряжение), по току (ток / ток), по сопротивлению (напряжение / ток), по проводимости (ток /напряжение ).

Для примера рассмотрим колебательный контур:

Q>>1

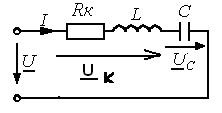
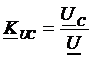
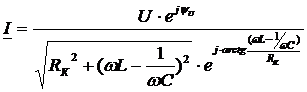
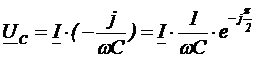
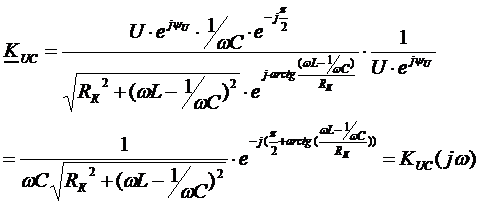
кривая пунктирная при Q<1,

при ω=ω₀ К₀=Q

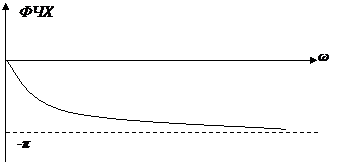
С использованием расстройки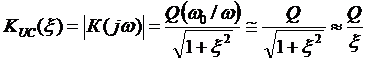

На избирательность контура

(Добротность, полоса пропускания, коэффициент подавления)

Внешним сопротивлением является сопротивление источника и нагрузки.

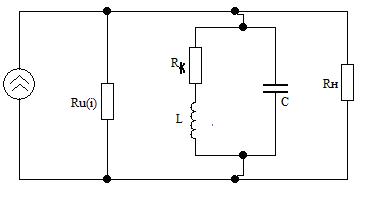
Резистор

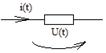
Индуктивность L

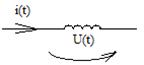
Для цепи общего вида

φ= ( Ψ_U-Ψ_I)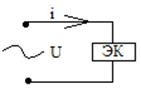

р(t)=Im·cos(ω·t)·Um·cos(ω·t+φ)

Pср=P=U·I·cosφ

Q= U·I·sinφ

Активная мощность P уходит из цепи в какую-то работу, а реактивная мощность Q возвращается назад.

cosφ - это технический параметр. Для энергетиков он имеет важное значение. Для них необходимо, чтобы cosφ был близок к 1.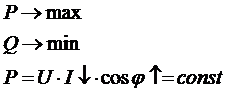

Полная мощность- это итоговая мощность в цепи и она измеряется в вольт-амперах - [В·А]. Она находится по формулам: S=U·I или

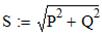, где P - активная мощность, а Q - реактивная мощность.

Активная энергия это энергия идущая на полезную работу, а реактивная энергия это энергия обмена между источником и потребителем обычно вредная энергия. Она излишне нагружает линии передачи энергии, что вызывает дополнительные потери в сопротивлении проводов. Поэтому стараются ее уменьшить.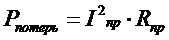

Ом, 75 Ом.

Связями и методы их расчета

Основные понятия о взаимной индукции

При расчете электрических цепей изображают схему замещения цепи, где направление обмоток и расположение их в пространстве конкретно не показывают и определить направление магнитных потоков и тип включения невозможно.

В связи с этим вводят специальное понятие одноименных или однополярных зажимов пары взаимо - индуктивно (магнитно) связанных элементов, которые специальным знаком указываются на схемах, например, точкой.

Связанных элементов

1. Последовательное соединение

Изобразим схему замещения последовательно магнитно связанных элементов. Здесь может быть 2 варианта расположения одноименных зажимов – согласное (одноименные зажимы с одной стороны обмоток) и встречное (с разных сторон).

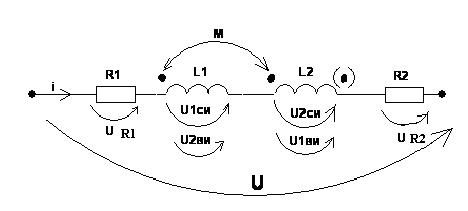
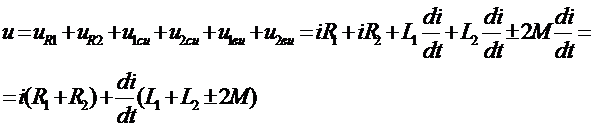
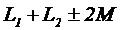- эквивалентная (общая) индуктивность. При согласном включении используется знак +, а при встречном, когда одноименный зажим показан на противоположном конце второй индуктивности ставится знак -.

2. Параллельное соединение

Электрический трансформатор

Электрический трансформатор – это устройство, которое трансформирует (преобразует) электрическое напряжение, ток или сопротивление с помощью явления взаимной индукции и содержит две или более индуктивно-связанных обмоток. Может иметь сердечник из магнитного или немагнитного материала.

1. Идеальный трансформатор при гармоническом воздействии.

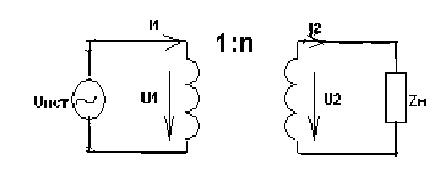
n – коэффициент трансформации, Z_Н - сопротивление нагрузки.

Для идеального трансформатора всегда выполняется условие:

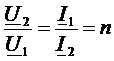- некоторое вещественное число

Говорят, что трансформатор трансформирует напряжение в n раз, а ток в 1/n. Мощность не меняется: - на входе и на выходе она одинакова. Рассмотрим входное сопротивление ИТ.

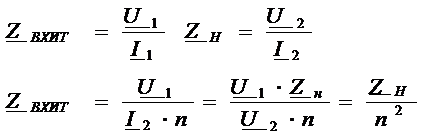- трансформация сопротивления в 1/n² .

Здесь при указанных одноименных зажимах сверху индуктивностей и направлений токов получается встречное включение (токи протекают противоположно относительно исходного положения точек). Знак в скобках ставится при расположении одноименного зажима внизу второй обмотки, который также показан в скобках.

Рассмотрим различные режимы работы трансформатора:

1) 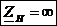- холостой ход. Тогда

.

.

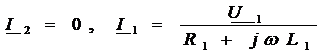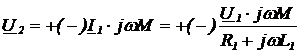Если хороший трансформатор, то 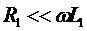и можно принять R₁=0.

.

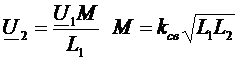У хорошего трансформатора k_св=1, а величина индуктивностей пропорциональна квадрату числа витков.

.

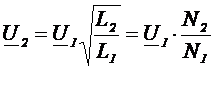
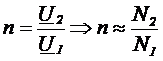Основные понятия о переходных процессах

Законы коммутации

Суммарное потокосцепление индуктивных элементов в цепи не может изменяться скачком в момент коммутации и является непрерывной функцией времени. В момент коммутации оно равно непосредственному значению перед коммутацией и непосредственному значению после коммутации.

Используя начальные условия

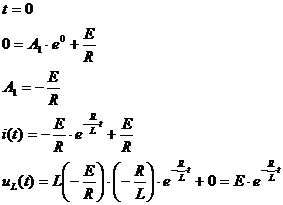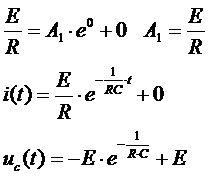Последовательная RLC цепь

Закон Кирхгофа

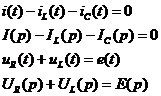
Закон Кирхгофа.

Для емкости получим

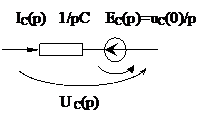
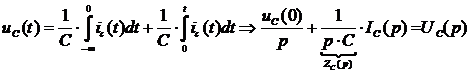
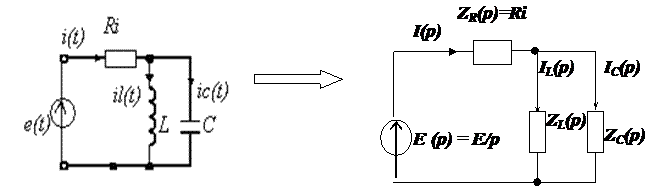
Технически это значит нахождение откликов или реакций электрической цепи при каких-то коммутациях, т.е. зависимости токов или напряжений в электрических цепях. В общем, это математическая процедура нахождения оригинала по операторному изображению.

Теоретически можно выделить три способа нахождения:

· по обратному преобразованию Лапласа.

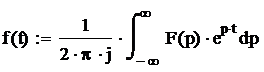
· табличным способом.

АЧХ показывает как изменяется отношение амплитуд выходного и входного сигнала электрической цепи при гармоническом воздействии. Фазо - частотная характеристика (ФЧХ) показывает как изменяется разность фаз выходного и входного сигнала электрической цепи при гармоническом воздействии. (Все это при изменении частоты.) Частотная характеристика показывает частотные свойства электрической цепи.

При расчете передаточных функций используются законы Ома и Кирхгофа в операторной и комплексной форме обычно при нулевых условиях в зависимости от характеристики. Для сложных цепей приминаются некоторые специальные методы: метод контурных токов, метод узловых напряжений и т.п в операторном виде.

Под ними понимают функции времени численно равные реакции электрической цепи на стандартное воздействие на цепь. Применяются обычно для линейных цепей при нулевых условиях (без запаса энергии в цепи).

1. Единичная ступенчатая функция или функция Хевисайда. Определяется следующим способом:

σ(t) =1(t)

σ(t) = 0, t<0

σ(t) = 1, t>0

2. Единичная импульсная функция или функция Дирака.

δ(t)=0, t<0

δ(t)= ¥, t=0

δ(t)=0, t>0

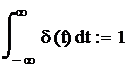
Ее можно рассматривать как предел импульсного сигнала такого вида:

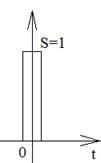t_U=Δt, U_u=1/Δt, Δt→0

В соответствии с испытательными (стандартными) сигналами используются две характеристики:

1. Переходная характеристика - это функция времени, численно равная реакции электрической цепи на единичное ступенчатое воздействие.

h(t) = k(t) = g_σ(t)

Различают в зависимости от типа воздействия и реакции четыре вида переходных характеристик: по напряжению, по току, по сопротивлению и по проводимости.

Переходная характеристика.

· Можно рассчитать классическим методом, подключая ко входу цепи (t=0) источник напряжения (1В) или тока (1А) и рассчитывать ток или напряжение на выходе.

· Можно операторным методом. Аналогично рассчитывать ток или напряжение.

I₂(p) ¸>

U₂(p) ¸> с учетом что на входе U₁(p)= 1/p, потом u₂(t).

· Можно рассчитать через коэффициент передачи.

h (t) ¸ K(p)/p, h(t) = k(t) , U₂(p) = K(p)·U₁(p).

Если найдем оригинал U₂(p) получим переходную характеристику.

· Применяя какие-либо программные средства.

· Экспериментальным путем (по осциллографу).

Импульсная характеристика.

· Классический метод не пригоден, т.к. воздействие бесконечно.

· Операторный метод использовать можно. Здесь изображение воздействия 1.

· Через К(р)

… F₁(p) / F₂(p) = K(p)

g(t) ¸ K(p) Удобно для стандартных цепей.

Программные средства

Пример нахождения временных характеристик

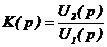
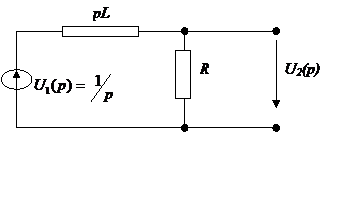
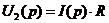
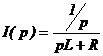
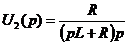
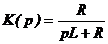
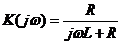
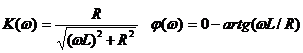
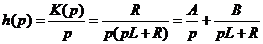
Определив коэффициенты A и B, получаем: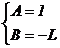

Тогда: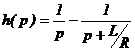

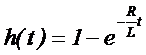
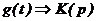
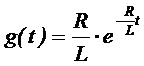
ω=2πf

Классический метод

Можно рассчитывать отдельно на включение импульса и на выключение, если за время импульса переходный процесс закончится.

Операторный метод

Находим X(p)=(по Лапласу)

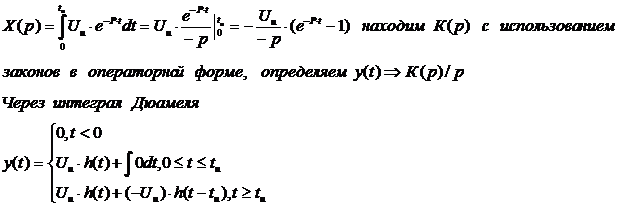
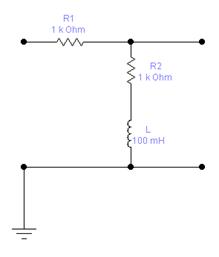Возьмем для примера цепь:

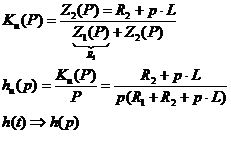
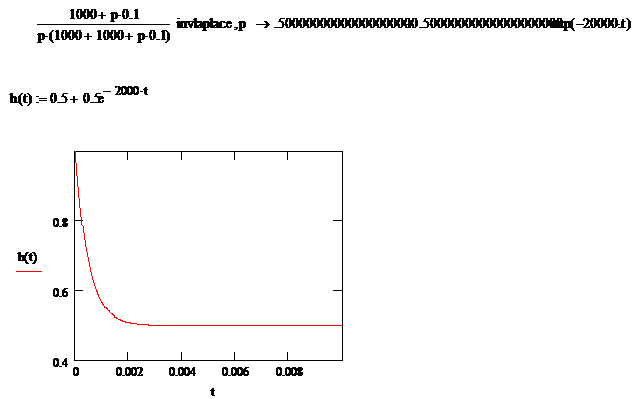
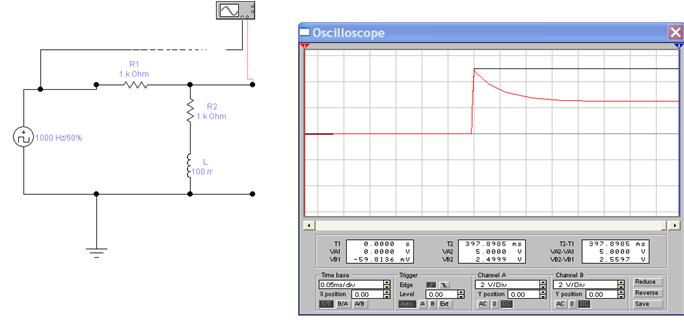
Общие понятия

При обработке электрических сигналов может возникнуть задача дифференцирования или интегрирования сигнала, т.е. чтобы реакция на выходе цепи была пропорциональна производной или интегралу входного сигнала.

Дифференцирующими и интегрирующими называют цепи, которые имеют на выходе напряжение, пропорциональное производной или интегралу от входного напряжения.

Дифференцирующие цепи

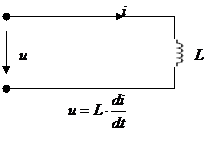
Аналогично RL-цепь.

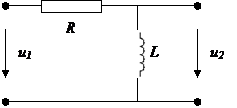
В данном случае должны выполняться условия: 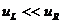, сопротивление должно быть большим, а индуктивность малой. В итоге постоянная времени малая.

Используют и такие цепи

С точки зрения ТЦ операционный усилитель (ОУ) – это ИНУН, у которого коэффициент усиления .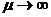

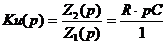
Умножение на p говорит о дифференцировании. Следовательно, это дифференцирующая цепь. Здесь на выходе будет достаточно большое напряжение.

Интегрирующие цепи

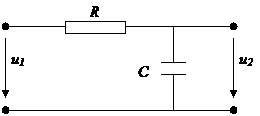Условия:

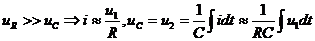
Если длительность уменьшается, то основная частота не изменится, нулевые точки переместятся вправо. До первой нулевой точки, где сосредоточена основная энергия, попадает больше составляющих. Технически отмечают, что спектр расширяется.

Непериодический сигнал можно разбить на бесконечную сумму гармонических составляющих с бесконечно малыми амплитудами и отличающихся по частоте на бесконечно малые величины – Это называется сплошным спектром не периодичес