Статистическое исследование связей между явлениями

Корреляция- это статическая зависимость между случайными величинами, не имеющая строго функционального характера, при котором изменение одной из случайных величин приводит к изменению математического ожидания другой.

Корреляционная связь- это связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.

Факторный признак- это признак, обуславливающий изменение других, связанных с ними признаков, а признаки, изменяющиеся под действием факторных признаков, являются результативными.

По степени тесноты связи различают количественные критерии оценки тесноты связи (табл.6)

Величина коэффициента корреляции	Характер связи
До ± 0.3	Практически отсутствует
± 0.3 - ± 0.5	слабая
± 0.5 - ± 0.7	умеренная
± 0.7 - ± 1.0	сильная

Для изучения корреляционной связи применяют метод аналитической группировки. Чтобы выявить зависимость с помощью этого метода, нужно провести группировку единиц совокупности по факторному признаку, и для каждой группы вычислить среднее значение результативного признака.

По аналитическому выражению выделяют прямолинейные (линейные) и нелинейные. Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью; если же она выражается уравнением кривой линии, то такую связь называют криволинейной.

Помимо метода аналитических группировок для оценки тесноты связи применяется такой показатель как линейный коэффициент корреляции.

Коэффициент корреляции рассчитывается по формуле

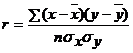, (3.1)

где x- отдельные значения факторного признака, положенного в основание группировки;

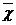- среднее значение факторного признака;

y - отдельные значения результативного признака;

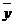- среднее значение результативного признака;

n - число наблюдений.

Для практических вычислений при малом числе наблюдений линейный коэффициент корреляции исчисляют по формуле

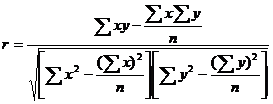. (3.2)

Коэффициент корреляции принимает значения в интервале -1£ r ³ 1.

Отрицательное значение указывает на обратную связь, положительное - на прямую. При r = 0 – линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине = 1, тем теснее связь между признаками. При r =± 1 связь - функциональная.

Пример 5

По пяти однотипным предприятиям (табл.7) имеются следующие данные о выпуске продукции (х) в тыс. ед. и о расходе условного топлива (y) в тоннах.

Таблица 7- Данные о выпуске продукции и расходе топлива

х.
y

С помощью линейного коэффициента корреляции определить наличие связи между расходом топлива и выпуском продукции.

Решение:

1. Построим макет таблицы

х	y		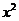	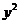хy

r = 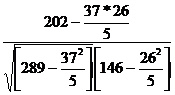= = 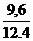0.77

Вывод: Связь между выпуском продукции и расходом топлива – сильная.

4. Ряды динамики.

Ряды динамики – это ряды с изменяющимися во времени значениями статистических показателей, расположенных в хронологическом порядке.

Составными элементами ряда динамики являются показатели уровней ряда и периоды времени (года, кварталы, месяцы, сутки) или моменты (даты) времени.

Уровни ряда обычно обозначаются через “у”, моменты или периоды времени, к которым относятся уровни, - через “t ”.

Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся:

- абсолютный прирост;

- темп роста;

- темп прироста.

Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение - базисным.

Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо первоначальный уровень, в ряду динамики, либо какой-то новый этап развития явления. Такие показатели называются базисными.

Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа называются цепными.

Абсолютный прирост (сокращение) характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени.

Для характеристики интенсивности, т.е. относительного уменьшения, уровня динамического ряда за к.л. период времени, исчисляют темпы роста (снижение). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.

Показатель интенсивности изменения уровня ряда выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели изменения отличаются только единицами измерения.

Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение.

Темп роста всегда представляет собой положительное число.

Относительную оценку скорости измерения уровня ряда динамики в единицу времени дают показатели темпа прироста (сокращения).

Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.

Темп прироста может быть положительным, отрицательным или равным нулю, и выражается в процентах или долях единицы (коэффициент прироста).

Показатели изменения уровней ряда динамики могут быть исчислены по формулам

Абсолютный прирост

Цепной Базисный

, ,

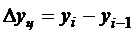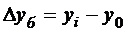где y_i – уровень сравниваемого периода;

y_i-1 – уровень предшествующего периода;

y₀ – уровень базисного периода.

Коэффициент роста

Цепной Базисный

, .

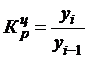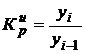Темп роста (сокращения)

цепной Базисный

, .

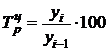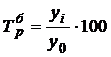Темп прироста (сокращения)

Цепной Базисный

, .

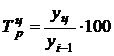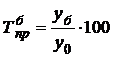или

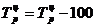
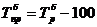
Коэффициент прироста

, .

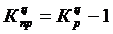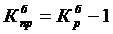Средний абсолютный прирост( 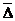у)– обобщающая характеристика ряда динамики, служащая для сравнения скорости развития разных рядов. Показатель определяется по формуле

,

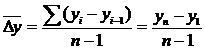где у_n – последнее значение уровня ряда динамики;

у₁ – первое значение уровня ряда;

n – число уровней ряда.

Средний коэффициент ростапоказывает, во сколько раз в среднем за единицу времени изменится уровень ряда динамики.

;

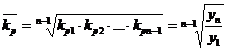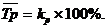
Средний темп прироста ( 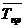)характеризует среднюю интенсивность изменения уровней ряда динамики

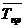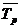= – 100% = (k_р – 1) ∙100%

и является сводной характеристикой развития явления.

Индексы

Под индексом понимают относительный показатель, характеризующий изменение величины к.л. явления во времени, пространстве или по сравнению с любым эталоном (нормативом, планом и т.д.).

В теории индексного метода применяют следующие обозначения:

1 – подстрочный символ показателя текущего (отчетного) периода;

0 – подстрочный символ предшествующего (базисного) периода;

i - индивидуальный индекс;

I – сводный (агрегатный) индекс

Р – цена ( розничная или оптовая);

q –количество (товара или выпущенной продукции);

z – себестоимость продукции;

t – трудоемкость единицы продукции;

pq –товарооборот;

zq – издержки производства;

По степени охвата единиц совокупности индексы делятся на 2 класса: индивидуальные и общие.

Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления.

Общий индексотражает изменение всех элементов сложного явления. Под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (цепи на разные группы продуктов и т.д.).

Общие индексы м.б. построены двумя способами: как средние из индивидуальных и как агрегатные.

Агрегатный индекс является основной формой индекса. Агрегатным он называется потому, что его числитель и знаменатель представляют набор непосредственно несоизмеримых и не поддерживающихся суммированию элементов – сумму произведений двух величин, одна из которых меняется, а другая остается неизменной в числителе и в знаменателе (вес индекса).

Индивидуальные индексы определяют вычислением отношения двух индексированных величин.

Так индивидуальный индекс цены рассчитывается по формуле

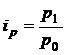, (5.1)

где P₁ – объем продукции в текущем периоде, т. руб.;

P₀ – объем продукции в базисном периоде, т. руб.

Индивидуальный индекс физического объема:

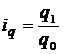, (5.2)

где q₁ – объем продукции в натуральном выражении текущего года;

q₀ - объем продукции в натуральном выражении базисного периода.

Определение стоимости продукции базисного периода 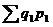к стоимости продукции текущего периода 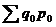представляет собой агрегатный индекс стоимости

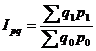(5.3)

Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным.

Если продукцию (товары) сравниваемых периодов оценивать одним и тем же базисным ценам p₀, то такой индекс отразит изменения только одного фактора – индексируемого показателя q₀ и будет представлять собой агрегатный индекс физического объема продукции

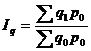. (5.4)

Индекс физического объема продукции показывает, во сколько раз объем продукции изменился в отчетном периоде по сравнению с базисным периодом.

Агрегатный индекс цен исчисляют по формуле:

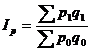. (5.5)

Индекс цен показывает, во сколько раз возрос (уменьшился) в среднем уровень цен отчетного периода по сравнению с базисным.

Разность числителя и знаменателя каждого индекса в правой части выражает изменение общей абсолютной величины под влиянием изменения одного фактора.

Общее изменение

.

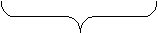
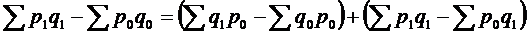D_qp

а) изменение товарооборота за счет цен: D_р = åp₁^. q₁ - å p₀ ^. q₁;

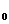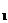
б) изменение товарооборота за счет объема: D_q = åp ^. q - å p₀ ^. q₀.

Пример 5

Заданы объем продукции базисного года (q₀ ) и отчетного года (q₁ ), а также цена продукции (p0, p1) по трем видам разнотипных изделий.

Определить индивидуальные и агрегатные индексы физического объема, цен, товарооборота и влияние факторов цены и объема на общее изменение показателя товарооборота (D_qp).

Таблица 8 -Расчет влияния факторов на абсолютное и относительное изменение показателя товарооборота

Вид продукции	Базисный период	Текущий период	Индивид. индексы	Стоимость продукции, тыс. руб.
Цена ед. прод., р   р0	Объем прод.,тыс. ед., q0	Цена ед. прод., р. р1	Объем прод., тыс. ед., q1	цен, %	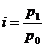физич. объема,	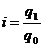базисного периода в ценах баз. периода q0p0	текущего периода в ценах
базисного периода q1p0	ткущего периода q1p1
А, шт Б, шт. В, шт	2,0 5,0 13,0		1,8 4,9 13,0			88,2 120,0
Итого	-		-		-	-

Решение:

1) Определим агрегатные индексы физического объема (Iq), цены (Iр), товарооборота (Iрq), воспользуясь расчетными данными таблицы 8:

Iq = 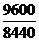* 100= 113,7%; Iр= 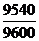*100 =99,3%

Iрq= 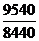*100 = 113,03%

2) Решим задачу с учетом влияния факторов структуры.

а) за счет изменения объемов продукции:

D_q= 9600 -8440 = 1160 тыс. руб;

б) за счет изменения цены:

D_р= 9540 –9600 = - 60 тыс. руб.

в) за счет влияния двух факторов:

D_qр= 9540 -8440 = 1100 тыс. руб.

Вывод: Товарооборот за счет изменения объемов продукции увеличился на 1160 тыс. руб. или на 13,7%, за счет изменения цены – снизился на 60 тыс. руб. или на 0,7%, за счет влияния обоих факторов увеличился на 1100 тыс. руб. или на 13,0%.

Задания контрольной работы

Задача 1

По предприятию №-города имеются соответствующие данные за отчетный год (табл.1).

Требуется:

1) сделать структурную группировку,

2) определить по каждой группе и в целом, среднее значение варьирующего признака. Результаты группировки представить в виде статической таблицы. Сделать вывод.

Таблица 1. Исходные данные (условные)

В	№ Пред- приятия
Объем продукц млн.кг.	55,5	32,0	43,8	66,2	35,6	20,1	85,1	63,4	29,0	46,6	38,0	36,0	40,5	21.4	84,7	91,0
	Выручка млн. руб
	Уставн. капитал, млн. р.	0,1	0,3	0,15	1,0	0,99	0,4	0,55	0,66	0,7	0,81	0,41	0,17	0,33	0,5	0,27	0,38
	Прибыль тыс. руб.
	Объем продукц млн. руб.
	Выработкаруб/чел.
	Уставн. капиталмлн. р.
	Прибыль тыс. руб.	5,5.	8,0	4,4	3,9	2,2	4,7	3,3	6,4	2,3	3,3	6,7	5,5	3,6	4,0	2,8	2,9
	Себестоимость, тыс. руб
	Издержкимлн. руб	0,9	1,5	2,7	0,8	3,4	2,8	1,6	1,9	3,3	2,4	2,2	1,7	3,0	1,7	3.0	2,5

Задача №2

В целях изучения затрат времени на изготовление одной детали (трудоемкости) рабочими завода было проведено исследование, в результате которого получено следующее распределение деталей по затратам времени:

Вариант 1 Вариант 2

Трудоемкость, мин.	Число деталей, шт.
До 20
От 20 до 24
От 24 до 28

Трудоемкость,мин.	Число деталей, шт.
5-10
10-15
15-20

Вариант 3 Вариант 4

Трудоемкость,мин.	Число деталей, шт.		Трудоемкость, мин.	Число деталей, шт.
40-46		10- 20
46-52		20-30
Вариант 5	Вариант 6
Трудоемкость,мин.	Число деталей, шт.		Трудоемкость,мин.	Число деталей, шт.
До 3		100-150
От 3 до 6		150-200
От 6 до 9		200-250

Вариант 7 Вариант 8

Трудоемкость,мин.	Число деталей, шт.
До 20
От 20 до 24
От 24 до 28

Трудоемкость,мин.	Число деталей, шт.
До 20
От 20 до 24
От 24 до 28

Вариант 9 Вариант 10

Трудоемкость,мин.	Число деталей, шт.
До 20
От 20 до 30
От 30до 40

Трудоемкость,мин.	Число деталей, шт.
11-13
13-17
17-23

На основании данных вычислите:

1. Показатели вариации.

2. Общую дисперсию через правило сложения дисперсий.

3. Сделайте выводы об однородности совокупности;

Задача №3.

По отделениям фирмы (i – порядковый номер отделения) имеются соответствующие данные о прибыли (y,тыс. руб.) и себестоимости продукции ( x, тыс. р.)

Статистические данные приведены в таблице.

1) построить аналитическую таблицу и дать графическое изображение линии связи.

2) измерить тесноту связи между признаками с помощью коэффициента корреляции и сделать вывод о тесноте связи.

Вариант № 3.1.

i

yi

xi

Вариант № 3.2.

i

yi

xi

Вариант № 3.3

i

yi

xi

Вариант № 3.4.

i

yi

xi

Вариант № 3.5.

i

yi

xi

Вариант № 3.6.

i

yi

xi

Вариант № 3.7.

i

yi

xi

Вариант № 3.8.

i

yi

xi

Вариант № 3.9.

i

yi

xi

.

Вариант № 3.0.

i

yi

xi

Задача №4

Выручка предприятия по годам характеризуется следующими данными, млн.руб:

Годы	Выручка
Варианты
	0,2				1,1		0,1		3,4
	0,4				1,25		0,25		4,1
	0,5				1,5		0,3		5,6
	0,7				1,52		0,41		6,1
	0,79				1,6		0,5		6,6

Для анализа выручки предприятия следует вычислить:

1. Абсолютные приросты, темпы роста и темпы прироста (на цепной и базисной основе). Полученные показатели представьте в таблице.

2. Среднегодовое производство продукции;

3. Среднегодовой темп роста и прироста производства продукции.

Сделайте выводы.

4. Предполагая, что выявленная закономерность сохранится и в дальнейшем,

спрогнозировать объем вкладов в следующем за исследуемом периодом

месяца, используя закономерности:

а) средний абсолютный прирост;

б) средний темп роста;

Задача № 5

По предприятию имеются данные по 3-м видам продукции (А, Б, В), об объеме продукции и себестоимости в базисном и отчетном периодах

Требуется определить:

1) индивидуальные индексы физического объема и себестоимости.

2) агрегатный индекс физического объема и себестоимости.

3) экономию (или увеличение) издержек производства в связи с изменением себестоимости.

Вари ант	вид	Объем продаж тыс. ед.	Себестоимость ед. продукции, тыс.р.
Продукт	В базисном периоде	В отчетном периоде	В базисном периоде	В базисном периоде
	А, кг
Б, шт
В,.т	0,2	0,5
	А, кг
Б тыс. м
В, шт..
	А, кг
Б, шт
В, т
	А, кг				2,8
Б, шт				1,5
В,.т	1,5
	А, кг
Б, шт
В,т
	А, кг
Б, шт
В, т
	А, кг	2,5
Б, шт	3,7
В, т
	А, кг			1,2	1,5
Б, шт
В, т			5,7
	А, кг
Б, шт
В, т
	А, кг
Б, шт
В, т
	А, кг
Б, шт
В, т

Библиографический список

Основная литература

1. Васильева Э.К., Лялин В.С. Статистика: Учебник для студентов, обучающихся по специальностям экономики и управления (080100) [Текст] / Э.К.Васильева, В.С.Лялин, М.:ЮНИТИ-ДАНА, 2007. 399с.

2. Гусаров В.М., Кузнецова Е.И. Статистика: учебное пособие для студентов вузов, обучающихся по экономическим специальностям [Текст] / В.М. Гусаров, Е.И.Кузнецова.-2-е изд.,перераб. и доп. М.: ЮНИТИ-ДАНА, 2007. 479с.

3. Елисеева И.И. Статистика: Учебник для вузов [Текст] /И.И.Елисеева. – М.: ТК Велби, изд-во Проспект, 2005. 385с.

4. Неганова Л.М. Статистика: конспект лекций [Текст] / Л.М.Неганова. – М.: изд-во Юрайт, 2010.220с.

Дополнительная литература

1. Баклушина О.А. Краткий курс по экономической статистике: учеб.пособие [Текст] / О.А.Баклушина. М.: Иэд-во Окей-книга, 2009. 144с.

2. Башкатов Б.И., Рябушкин Б.Т. Практикум по национальному счетоводству: учеб.пособие

[Текст] / Под ред. Б.И.Башкатова. М.: Финансы и статистика, 2004. 320с.

3. Блинова В.С. Статистика в вопросах и ответах: учеб.пособие [Текст] / В.С.Блинова. М.: ТК

Велби, Изд-во Проспект, 2004. 344с.

4. Голуб Л.А. Социально-экономическая статистика: учеб.пособие для студентов высш. учеб. Заведений [Текст] / Л.А.Голуб. М.: Гуманитарный издательский центр ВЛАДОС, 2001.272с.

5. Голышев А.В. Краткий курс по статистике: учеб.пособие [Текст] / А.В.Голышев.- 2-е изд. М.: Изд-во Окей-книга, 2008. 188с.

6. Громыко Г.Л. Теория статистики: Практикум [Текст] / Г.Л.Громыко.- 3-е изд.перераб. и доп. М.: ИНФРА-М, 2004. 368с.

7. Елисеева И.И. Практикум по макроэкономической статистике: учеб.пособие [Текст] / И.И.Елисеева, С.А. Силаева, А.Н .Щирина. М.: ТК Велби, Изд-во Проспект, 2007. 288с.

8. Колесникова И.И., Круглякова Г.В. Статистика: учеб.пособие [Текст] /И.И.Колесникова, Г.В.Круглякова. М.: Новое знание, 2005. 208с.

9. Неганова Л.М. Общая теория статистики: учеб.пособие [Текст] /Л.М.Неганова. М.: Изд-во РИОР, 2007. 96с.

10. Татарников Е.А. Система национального счетоводства: конспект лекций [Текст] /Е.А.Татарников. М.: ПРИОР – ИЗДАТ, 2004. 80с.

11. Чижова Л.П. Практикум по социально-экономической статистике: учеб.пособие [Текст] /Л.П.Чижова. М.: ИТК «Дашков и К», 2003. 188с.

12. Экономическая статистика: Учебник [Текст] / Под ред.Ю.Н.Иванова.- 2-е изд.,доп. – М.: ИНФРА-М, 2004. 480с.

Задания к контрольным работам

по дисциплине

«Статистика»