И методические указания для их выполнения
Задания к контрольным работам
по дисциплине
«Статистика»
И методические указания для их выполнения
для студентов
заочной формы обучения
специализации «Оценка собственности»
специальности 080503.65 Антикризисное управление (351000);
специальности 080111.65 Маркетинг (061500);
специальности 050501.65 Профессиональное обучение
(экономика и управление) (030500.18);
специализации «Управление финансами на предприятии машиностроения»
специальности 080502.65 Экономика и управление на предприятии
(машиностроение) (060800(м));
специальности 080101.65 Экономическая теория (060100);
специальности 071103.65 Продюсерство кино и телевидения (053700)
Екатеринбург 2010
Задания к контрольным работам по дисциплине «Статистика» и методические указания для их выполнения (ГОС – 2000). Екатеринбург, ГОУ ВПО «Рос. гос. проф.-пед. университет», 2010. 27 с.
Составитель ст.преподаватель Логинова С.Л.
Одобрены на заседании кафедры экономической теории Института экономики и управления РГППУ. Протокол от « 28 » января2010 г. № 6.
Заведующий кафедрой А.Г. Мокроносов
Рекомендованы к печати методической комиссией Института экономики и управления РГППУ. Протокол от « 18 » февраля 2010 г. № 6 .
Председатель
методической комиссии ИнЭУ Ф.Д. Босько
© ГОУ ВПО «Российский
государственный
профессионально-
педагогический
университет», 2010
Введение
В соответствии с учебным планом студенты заочного факультета полной формы обучения выполняют контрольную работу по курсу «Статистика». Последние годы роль статистического образования возрастает во всем мире. Не в последнюю очередь это обусловлено возрастающей потребностью в умении пользоваться статистической информацией для принятия решений в политике, экономике и других видах деятельности. Поэтому, статистика, как наука, выполняет важнейшую функцию в формировании специалистов, особенно, экономического профиля и объединяет многие другие изучаемые в вузе дисциплины.
Цель контрольной работы – оценка эффективности усвоения программного материала учебной дисциплины и качества знаний студентов.
Задачи контрольной работы:
- закрепление и проверка знаний, полученных студентами в процессе самостоятельного изучения учебного материала по данной дисциплине;
- выявление их умения применять полученные теоретические знания на практике;
-развитие у студентов статистического мышления, навыков построения статистических таблиц и графиков;
-развитие навыков выявления связей между социально-экономическими явлениями;
- закрепление у студентов навыков работы со специальной литературой
Задание для контрольной работы представлены в виде 10 вариантов, каждый из которых включает пять задач.
Контрольная работа заключается в решении этих задач в указанной последовательности по соответствующему варианту.
При выполнении контрольной работы нужно соблюдать следующие требования:
1. Вариант контрольной работы следует выбирать по последней цифре номера зачетной книжки. Каждому варианту соответствуют данные таблицы каждой задачи.
2. В начале работ должен быть указан вариант задания.
3. Перед решением задачи необходимо полностью привести ее условие.
4. Решение задач следует сопровождать необходимыми формулами, таблицами, развернутыми расчетами, пояснениями, обоснованием хода решения и анализом полученных результатов.
5. Контрольная работа должна быть оформлена аккуратно в тетради в клеточку или на листах формата А4, написана разборчиво, без исправлений и помарок. Весь графический материал должен быть выполнен с помощью линейки. Работа может быть написана вручную или на компьютере. В конце работы следует указать список использованной литературы.
6. На обложке тетради должны быть четко написаны название дисциплины, фамилия студента, его инициалы, номер группы и шифр специальности, номер зачетной книжки.
7. В конце работы должна стоять подпись студента и указана дата выполнения работы.
Выполненную работу студенты сдают в деканат заочного факультета для проверки ее преподавателем курса «Статистика». Студенты, успешно выполнившие контрольную работу и получившие по ней зачет, допускаются к экзамену по данному курсу. Студенты, не получившие зачета по контрольной работе, вносят в нее необходимые исправления и вновь сдают на проверку в установленном порядке.
Группировкой называется расчленение множества единиц изучаемой совокупности на группы по определенным существенным для них признакам.
Пример 1
Требуется произвести группировку с равными интервалами предприятий по величине Уставного капитала, при этом максимальное значение признака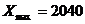 
млн р., минимальное X 
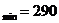млн р. Совокупность включает 20 единиц.
Решение:
1) Определение числа групп. В основании группировки заложен количественный признак, поэтому определяем по формуле 1. или таблице 1
n = 1 + 3,322lg20 = 5
2) Расчет величины интервала
h =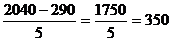 
млн р.
Таблица 2 – Структурная группировка по величине Уставного капитала
| Номер групп | 1 вариант (закрытые интервалы) | 2 вариант (открытые интервалы) | Число предприятий | % к итогу |
| I | От 290 до 640 | До 640 | ||
| II | От 640 до 990 | 640-990 | ||
| III | От 990 до 1340 | 990 - 1340 | ||
| IV | От 1340 до 1690 | 1340 -1690 | ||
| V | От 1690 до 2040 | 1690 - 2040 | ||
| Итого |
Средние величины
Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину выросшего признака в расчете на единицу качественно однородной совокупности.
Средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц.
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая и т.д.
Наиболее распространенным видом средних величин является средняя арифметическая.Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц.
Чтобы рассчитать среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.
Средняя арифметическая величина применяется в форме простой средней и взвешенной средней.
Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, делимой на общее число этих значений (она применяетсяв тех случаях, когда имеются не сгруппированные индивидуальные значения признака).
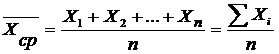, (1.4)
где Х1,X2,Хn – индивидуальные значения варьирующего признака (варианты);
n - число единиц совокупности.
Для расчета средних сгруппированных индивидуальных значений признака совокупности применяется расчет средней арифметической взвешенной.
Средняя величина из вариантов, которые повторяют различное число раз, или, имеют различный вес, называются взвешенной. В качестве весов выступают численности единиц в разных группах совокупности.
Средняя арифметическая взвешенная – средняя сгруппированных величин выполняется по формуле
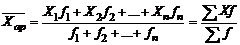, (1.5)
где X1,X2, X п- отдельные значение признака;
f1 f2 f3 - веса/частоты повторения одинаковых признаков,
Σ xf - сумма произведений величин признаков на их частоты;
Σf - общая численность единиц совокупности.
Вычисление средней арифметической взвешенной из групповых средних Хгр осуществляется по формуле
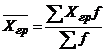, (1.6)
где f- число единиц каждой группе.
Если значения определяемого признака заданы в виде интервалов («от – до»), т.е. интервальных видов распределения, то при росте средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов. После того как найдены середины интервалов, вычисления делают так же при расчете средней взвешенной.
Пример 2
Имеются данные о распределении работников предприятия по возрасту (табл.3). Требуется определить средний возраст работников.
Данная группировка выполнена с открытыми интервалами. При определении середины интервалов границы открытых интервалов условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего).
Таблица 3 -Распределение работников предприятий по возрасту
| Возраст, лет | Середина интервала | Число работников, чел. |
| До 25 25-30 30-40 40-50 50-60 60 и более | 22,5 27,5 65 | |
| Итого: | – |
Решение:
Полученные средние значения интервала используются для расчета средней по совокупности
:
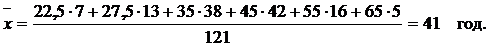
Показатели вариации
Вариация- это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней величины или значительно отклоняются от нее.
Потому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.
К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации (R)- разность между максимальным и минимальным значением признака в совокупности (см. формулу 1.3).
Среднее линейное отклонение (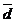 
) представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом виде предполагают, что среднюю вычисляют из варианта.
Среднее линейное отклонение рассчитывают по формуле:
а) для несгруппированных данных
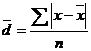, (2.1)
где х– отдельные значения признака (вариант);
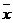- средняя величина по совокупности;
n – число членов ряда.
б) для сгруппированных данных
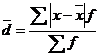, (2.2)
где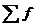 
- сумма частот вариационного ряда.
Дисперсия(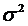 
) – это средний квадрат отклонений вариантов от их средней величины.
а) Простая дисперсия для несгруппированных данных
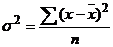, (2.3)
б) взвешенная дисперсия для вариационного ряда
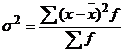. (2.4)
Среднее квадратическое отклонение (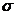 
) равно корню квадратному из дисперсии
а) для негруппированных данных
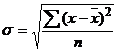, (2.5)
б) для вариационного ряда
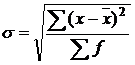. (2.6)
Среднее квадратическое отклонение показывает, на сколько в среднем откланяются конкретные варианты от их среднего значения.
Коэффициент вариации (γ) – выражен в % отношении среднего квадратического отклонения к средней арифметической
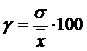. (2.7)
Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.
Правило сложения дисперсий
Общая дисперсия (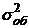 
) измеряет вариацию признака по всей совокупности под влиянием факторов, обусловивших эту вариацию.
Она равна среднему квадрату отклонений отдельных значений признака х от общей средней 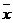и может быть вычислена как простая по (формуле 2.3) или взвешенная дисперсия (по формуле 2.4).
Межгрупповая дисперсия (δ2) характеризует систематическую вариацию результативного порядка, обусловленную влиянием факторного признака, положенного в основание группировки.
Определение по формуле
δ2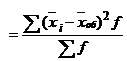 
, (2.8)
где xi– средняя по каждой группе;
xоб– средняя по совокупности
Внутригрупповая дисперсия 
( 
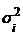) отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки
а) внутригрупповая дисперсия для негруппированных данных может быть исчислена по формуле
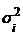
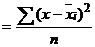, (2.9)
б) для сгруппированных данных
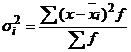. (2.10)
На основании внутригрупповой дисперсии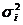 
можно определить общую среднюю из внутригрупповых дисперсий
.
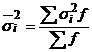Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий
.
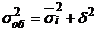Пример 3
Вычислить показатели вариации (s2 ,s, d, R,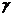 
) по следующим исходным данным (табл.4).
Таблица 4- Распределение рабочих-сдельщиков n-го цеха по фактической выработке деталей
| Дневная выработка деталей, шт. | Число рабочих-сдельщиков, чел. |  |  |  |  |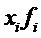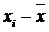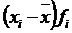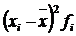
| -1,9 -0,9 0,1 1,1 2,1 | 55,1 29,7 7,9 51,7 25,2 | 104,69 26,73 0,79 56,87 52,92 | |||
| Итого: | – | 169,6 | 242,0 |
1)Находим среднюю по совокупности
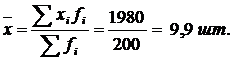
2) Размах вариации R = Xmax – Xmin , R = 12 – 8 = 4 шт.
3) Среднее линейное отклонение d =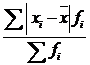 
= 
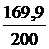= 0,848 шт.
Сравниваем отклонение с величиной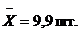 
Среднее отклонение вариантов признака от их средней величины несущественное, следовательно, совокупность в отношении признака однородна, а средняя типична для данной совокупности.
3) 
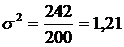; 4) 
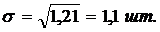
Среднее квадратическое отклонение невелико по сравнению с 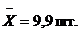Вывод тот же, что и при определении среднего линейного отклонения.
5) Коэффициент вариации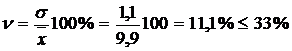 
,
следовательно, совокупность однородна.
Пример 4
Имеется производительность труда двух групп рабочих n-го цеха (табл.5).
Таблица 5 -Производительность труда 2-х групп рабочих n-го цеха
| Показатель | Рабочие, прошедшие техническое обучение | Рабочие, не прошедшие техническое обучение | ||||||||
| Выработка, дет./см. | ||||||||||
| Число рабочих, чел. |
Рассчитать три вида дисперсии, проверить правило сложения дисперсий.
Решение
Производительность труда – результативный признак. Численность – это частота.
Определим средние значения производительности труда
1) групповые средние
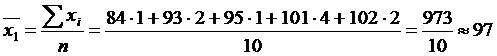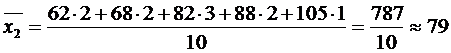дет.
дет.
2) общая средняя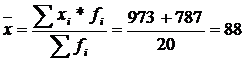 
дет.
Определим внутригрупповые дисперсии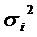 
(всего две группы, следовательно, дисперсий будет тоже две)
=
= 
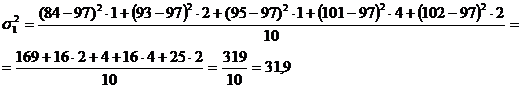
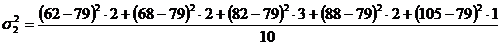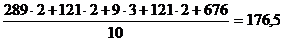
Межгрупповая дисперсия (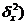 
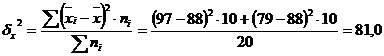
Средняя из внутригрупповых
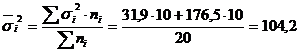
Общая дисперсия, рассчитанная с использованием правила сложения дисперсий, имеет следующее значение
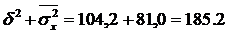
Общая дисперсия, рассчитанная по базовой формуле, дает тот же результат
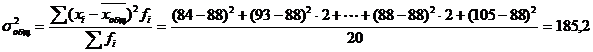
Эмпирическое корреляционное соотношение
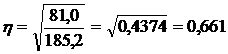
Вывод:Фактор технического обучения объясняет 66,1% вариации производительности труда.
Пример 5
По пяти однотипным предприятиям (табл.7) имеются следующие данные о выпуске продукции (х) в тыс. ед. и о расходе условного топлива (y) в тоннах.
Таблица 7- Данные о выпуске продукции и расходе топлива
| х. | |||||
| y |
С помощью линейного коэффициента корреляции определить наличие связи между расходом топлива и выпуском продукции.
Решение:
1. Построим макет таблицы
| х | y | 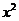 | 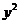 | хy |
r =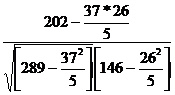 
= 
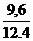= 0.77
Вывод: Связь между выпуском продукции и расходом топлива – сильная.
4. Ряды динамики.
Ряды динамики – это ряды с изменяющимися во времени значениями статистических показателей, расположенных в хронологическом порядке.
Составными элементами ряда динамики являются показатели уровней ряда и периоды времени (года, кварталы, месяцы, сутки) или моменты (даты) времени.
Уровни ряда обычно обозначаются через “у”, моменты или периоды времени, к которым относятся уровни, - через “t ”.
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся:
- абсолютный прирост;
- темп роста;
- темп прироста.
Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение - базисным.
Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо первоначальный уровень, в ряду динамики, либо какой-то новый этап развития явления. Такие показатели называются базисными.
Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа называются цепными.
Абсолютный прирост (сокращение) характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени.
Для характеристики интенсивности, т.е. относительного уменьшения, уровня динамического ряда за к.л. период времени, исчисляют темпы роста (снижение). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.
Показатель интенсивности изменения уровня ряда выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели изменения отличаются только единицами измерения.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение.
Темп роста всегда представляет собой положительное число.
Относительную оценку скорости измерения уровня ряда динамики в единицу времени дают показатели темпа прироста (сокращения).
Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.
Темп прироста может быть положительным, отрицательным или равным нулю, и выражается в процентах или долях единицы (коэффициент прироста).
Показатели изменения уровней ряда динамики могут быть исчислены по формулам
Абсолютный прирост
Цепной Базисный
, 
,
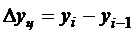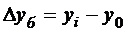где yi – уровень сравниваемого периода;
yi-1 – уровень предшествующего периода;
y0 – уровень базисного периода.
Коэффициент роста
Цепной Базисный
, 
.
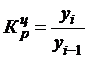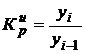Темп роста (сокращения)
цепной Базисный
, 
.
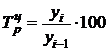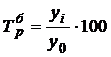Темп прироста (сокращения)
Цепной Базисный
, 
.
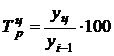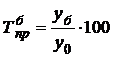или
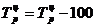
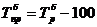
Коэффициент прироста
, 
.
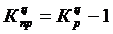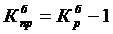Средний абсолютный прирост(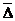 
у)– обобщающая характеристика ряда динамики, служащая для сравнения скорости развития разных рядов. Показатель определяется по формуле
,
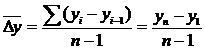где уn – последнее значение уровня ряда динамики;
у1 – первое значение уровня ряда;
n – число уровней ряда.
Средний коэффициент ростапоказывает, во сколько раз в среднем за единицу времени изменится уровень ряда динамики.
; 
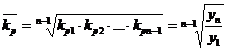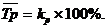
Средний темп прироста (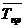 
)характеризует среднюю интенсивность изменения уровней ряда динамики
= 
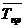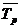– 100% = (kр – 1) ∙100%
и является сводной характеристикой развития явления.
Индексы
Под индексом понимают относительный показатель, характеризующий изменение величины к.л. явления во времени, пространстве или по сравнению с любым эталоном (нормативом, планом и т.д.).
В теории индексного метода применяют следующие обозначения:
1 – подстрочный символ показателя текущего (отчетного) периода;
0 – подстрочный символ предшествующего (базисного) периода;
i - индивидуальный индекс;
I – сводный (агрегатный) индекс
Р – цена ( розничная или оптовая);
q –количество (товара или выпущенной продукции);
z – себестоимость продукции;
t – трудоемкость единицы продукции;
pq –товарооборот;
zq – издержки производства;
По степени охвата единиц совокупности индексы делятся на 2 класса: индивидуальные и общие.
Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления.
Общий индексотражает изменение всех элементов сложного явления. Под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (цепи на разные группы продуктов и т.д.).
Общие индексы м.б. построены двумя способами: как средние из индивидуальных и как агрегатные.
Агрегатный индекс является основной формой индекса. Агрегатным он называется потому, что его числитель и знаменатель представляют набор непосредственно несоизмеримых и не поддерживающихся суммированию элементов – сумму произведений двух величин, одна из которых меняется, а другая остается неизменной в числителе и в знаменателе (вес индекса).
Индивидуальные индексы определяют вычислением отношения двух индексированных величин.
Так индивидуальный индекс цены рассчитывается по формуле
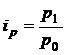, (5.1)
где P1 – объем продукции в текущем периоде, т. руб.;
P0 – объем продукции в базисном периоде, т. руб.
Индивидуальный индекс физического объема:
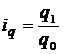, (5.2)
где q1 – объем продукции в натуральном выражении текущего года;
q0 - объем продукции в натуральном выражении базисного периода.
Определение стоимости продукции базисного периода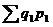 
к стоимости продукции текущего периода 
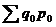представляет собой агрегатный индекс стоимости
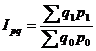(5.3)
Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным.
Если продукцию (товары) сравниваемых периодов оценивать одним и тем же базисным ценам p0, то такой индекс отразит изменения только одного фактора – индексируемого показателя q0 и будет представлять собой агрегатный индекс физического объема продукции
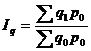. (5.4)
Индекс физического объема продукции показывает, во сколько раз объем продукции изменился в отчетном периоде по сравнению с базисным периодом.
Агрегатный индекс цен исчисляют по формуле:
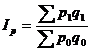. (5.5)
Индекс цен показывает, во сколько раз возрос (уменьшился) в среднем уровень цен отчетного периода по сравнению с базисным.
Разность числителя и знаменателя каждого индекса в правой части выражает изменение общей абсолютной величины под влиянием изменения одного фактора.
Общее изменение
.
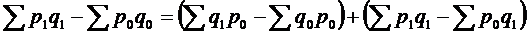Dqp
а) изменение товарооборота за счет цен: Dр = åp1. q1 - å p0 . q1;
б) изменение товарооборота за счет объема: Dq = åp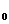 
. q 
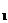
- å p0 . q0.
Пример 5
Заданы объем продукции базисного года (q0 ) и отчетного года (q1 ), а также цена продукции (p0, p1) по трем видам разнотипных изделий.
Определить индивидуальные и агрегатные индексы физического объема, цен, товарооборота и влияние факторов цены и объема на общее изменение показателя товарооборота (Dqp).
Таблица 8 -Расчет влияния факторов на абсолютное и относительное изменение показателя товарооборота
| Вид продукции | Базисный период | Текущий период | Индивид. индексы | Стоимость продукции, тыс. руб. | |||||
| Цена ед. прод., р р0 | Объем прод.,тыс. ед., q0 | Цена ед. прод., р. р1 | Объем прод., тыс. ед., q1 | цен, % 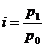 | физич. объема, 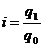 | базисного периода в ценах баз. периода q0p0 | текущего периода в ценах | ||
| базисного периода q1p0 | ткущего периода q1p1 | ||||||||
| А, шт Б, шт. В, шт | 2,0 5,0 13,0 | 1,8 4,9 13,0 | 88,2 120,0 | ||||||
| Итого | - | - | - | - |
Решение:
1) Определим агрегатные индексы физического объема (Iq), цены (Iр), товарооборота (Iрq), воспользуясь расчетными данными таблицы 8:
Iq =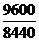 
* 100= 113,7%; Iр= 
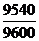*100 =99,3%
Iрq=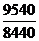 
*100 = 113,03%
2) Решим задачу с учетом влияния факторов структуры.
а) за счет изменения объемов продукции:
Dq= 9600 -8440 = 1160 тыс. руб;
б) за счет изменения цены:
Dр= 9540 –9600 = - 60 тыс. руб.
в) за счет влияния двух факторов:
Dqр= 9540 -8440 = 1100 тыс. руб.
Вывод: Товарооборот за счет изменения объемов продукции увеличился на 1160 тыс. руб. или на 13,7%, за счет изменения цены – снизился на 60 тыс. руб. или на 0,7%, за счет влияния обоих факторов увеличился на 1100 тыс. руб. или на 13,0%.
Задания контрольной работы
Задача 1
По предприятию №-города имеются соответствующие данные за отчетный год (табл.1).
Требуется:
1) сделать структурную группировку,
2) определить по каждой группе и в целом, среднее значение варьирующего признака. Результаты группировки представить в виде статической таблицы. Сделать вывод.
Таблица 1. Исходные данные (условные)
| В | № Пред- приятия | ||||||||||||||||
| Объем продукц млн.кг. | 55,5 | 32,0 | 43,8 | 66,2 | 35,6 | 20,1 | 85,1 | 63,4 | 29,0 | 46,6 | 38,0 | 36,0 | 40,5 | 21.4 | 84,7 | 91,0 | |
| Выручка млн. руб | |||||||||||||||||
| Уставн. капитал, млн. р. | 0,1 | 0,3 | 0,15 | 1,0 | 0,99 | 0,4 | 0,55 | 0,66 | 0,7 | 0,81 | 0,41 | 0,17 | 0,33 | 0,5 | 0,27 | 0,38 | |
| Прибыль тыс. руб. | |||||||||||||||||
| Объем продукц млн. руб. | |||||||||||||||||
| Выработкаруб/чел. | |||||||||||||||||
| Уставн. капиталмлн. р. | |||||||||||||||||
| Прибыль тыс. руб. | 5,5. | 8,0 | 4,4 | 3,9 | 2,2 | 4,7 | 3,3 | 6,4 | 2,3 | 3,3 | 6,7 | 5,5 | 3,6 | 4,0 | 2,8 | 2,9 | |
| Себестоимость, тыс. руб | |||||||||||||||||
| Издержкимлн. руб | 0,9 | 1,5 | 2,7 | 0,8 | 3,4 | 2,8 | 1,6 | 1,9 | 3,3 | 2,4 | 2,2 | 1,7 | 3,0 | 1,7 | 3.0 | 2,5 |
Задача №2
В целях изучения затрат времени на изготовление одной детали (трудоемкости) рабочими завода было проведено исследование, в результате которого получено следующее распределение деталей по затратам времени:
Вариант 1 Вариант 2
| Трудоемкость, мин. | Число деталей, шт. |
| До 20 | |
| От 20 до 24 | |
| От 24 до 28 |
| Трудоемкость,мин. | Число деталей, шт. |
| 5-10 | |
| 10-15 | |
| 15-20 |
Вариант 3 Вариант 4
| Трудоемкость,мин. | Число деталей, шт. | Трудоемкость, мин. | Число деталей, шт. | |
| 40-46 | 10- 20 | |||
| 46-52 | 20-30 | |||
| Вариант 5 | Вариант 6 | |||
| Трудоемкость,мин. | Число деталей, шт. | Трудоемкость,мин. | Число деталей, шт. | |
| До 3 | 100-150 | |||
| От 3 до 6 | 150-200 | |||
| От 6 до 9 | 200-250 |
Вариант 7 Вариант 8
| Трудоемкость,мин. | Число деталей, шт. |
| До 20 | |
| От 20 до 24 | |
| От 24 до 28 |
| Трудоемкость,мин. | Число деталей, шт. |
| До 20 | |
| От 20 до 24 | |
| От 24 до 28 |
Вариант 9 Вариант 10
| Трудоемкость,мин. | Число деталей, шт. |
| До 20 | |
| От 20 до 30 | |
| От 30до 40 |
| Трудоемкость,мин. | Число деталей, шт. |
| 11-13 | |
| 13-17 | |
| 17-23 |
На основании данных вычислите:
1. Показатели вариации.
2. Общую дисперсию через правило сложения дисперсий.
3. Сделайте выводы об однородности совокупности;
Задача №3.
По отделениям фирмы (i – порядковый номер отделения) имеются соответствующие данные о прибыли (y,тыс. руб.) и себестоимости продукции ( x, тыс. р.)
Статистические данные приведены в таблице.
1) построить аналитическую таблицу и дать графическое изображение линии связи.
2) измерить тесноту связи между признаками с помощью коэффициента корреляции и сделать вывод о тесноте связи.
Вариант № 3.1.
| i | |||||||||||||||
| yi | |||||||||||||||
| xi |
Вариант № 3.2.
i Наши рекомендации |