Тема 3. Силовой анализ плоских рычажных механизмов.

Задачи. Силы, действующие в машинах. Определение реакций в кинематических парах. Кинетостатика входного звена. Трение. Механический коэффициент полезного действия

Силы, действующие в машинах

Развитое машинное устройство, состоящее из двигателя, передаточных механизмов и рабочей машины и, в некоторых случаях, контрольно-управляющих машин, называется машинным агрегатом. К механизмам машинного агрегата во время его движения приложены различные силы. В зависимости от знака элементарной работы все эти силы подразделяются на силы движущие F_д (М _д ) и силы сопротивленияF _с (M_с), силы тяжести G и инерционные силы F_и (M_и), силы взаимодействия между k-тым и i-тым звеньями механизмов т.е. силы, действующие в кинематических парах (реакции в кинематических парах R_ki). Движущей силой называется сила, элементарная работа которой положительна, а силой сопротивления - сила элементарная работа которой отрицательна. Элементарная работа силы определяется как скалярное произведение силы на элементарное перемещения точки ее приложения. Силы сопротивления в свою очередь делятся на силы F_пс (или моменты сил M_пс) полезного сопротивления (силы, для преодоления которых предназначена данная машина) и силы F_вс (или моменты сил M_вс) вредного сопротивления(силы трения и силы сопротивления окружающей среды). Для определения силы трения рекомендуется использовать формулу Амонтона-Кулона. Силы тяжести G могут быть или силами движущими, или силами сопротивления в зависимости от направления перемещения центра тяжести звена.

Инерционные силы F_и и их моменты M_и определяются по известным из теоретической механике формулам:

F_и = -m×a_s,

M_и = - I_s×e,

где m – масса звена, кг;

a_s – ускорение центра масс звена, м/с²;

I_s – момент инерции звена относительно оси, проходящей че-

рез его центр масс перпендикулярно к плоскости движения, кг×м²;

e - угловое ускорение звена, с^-2.

Методы динамического анализа (исследования) в данном курсе рассматриваютсяприменительно к плоским механизмам с одной степенью свободы, которые являются наиболее распространенными. Одной из задач динамического анализа механизма является проведение кинетостатического (силового) расчета, при котором определяются реакции в кинематических парах и уравновешивающий момент (уравновешивающая сила), приложенный к исходному механизму от действия внешних сил и сил инерции.

Силовой расчет ведется с использованием принципа д'Аламбера методом планов сил по отдельным структурным группам Ассура, представляющих собой кинетостатически определимые системы (кинематические цепи). Для этих цепей число неизвестных реакций в кинематических парах равно числу условий кинетостатики. Знание реакций в кинематических парах необходимо для расчета звеньев механизма на прочность. Уравновешивающий момент обеспечивает заданный закон движения входного звена, а, следовательно, и всего механизма. Для технологических машин по уравновешивающему (движущему) моменту и частоте вращения входного звена определяется мощность приводного двигателя.

Силовой расчет

Силовой расчет начинается с последней, т.е. наиболее удаленной от ведущего звена группы Ассура, и кончается расчетом ведущего звена.

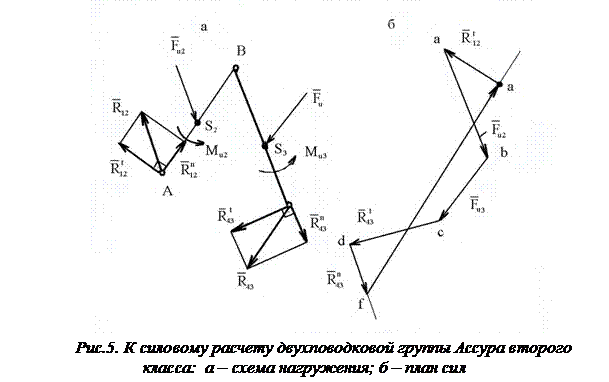
В качестве примера рассмотрим силовой расчет двухповодковой групп Ассура. На рис.5,а приведена схема двухповодковой группы второго класса первого вида. На звенья 2 и 3 действуют известные силы и моменты. В точках B и D прикладываем неизвестные реакции R₁₂ и R₄₃ отброшенных звеньев 1 и 4 на оставшиеся 2 и 3, условно направляя их вверх. Уравнение равновесия группы имеет вид

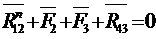
Разложим векторы реакций на составляющие по направлениям звеньев (нормальные) и перпендикулярно звеньям (тангенциальные):

; .

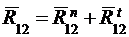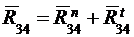Тогда уравнение равновесия примет вид

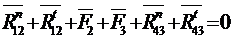
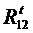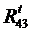Составляющие реакции и определяют из условия равновесия звеньев 2 и 3. Для этого составляют уравнения моментов для каждого из звеньев относительно точки C.

Для звена 2

M_C( 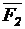) + M_C( 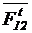) + M₂ = 0,

откуда

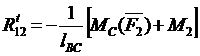
Для звена 3

M_C( 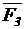) + M_C( 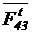) + M₃ = 0,

откуда

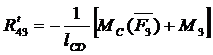
Составляющие реакци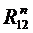й и 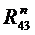и полные реакци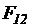и и 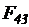определяем из плана сил (рис.5б), построенного на основе уравнения равновесия.

Из начала плана сил (точка а) в некотором масштабе m_F проводим вектор силы 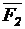и из его конца – вектор силы 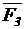.Из начала вектора 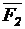и из конца вектора 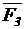проводим найденные выше силы 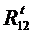^BC и 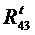^CD. Из точек d и e проводим линии в направлении сил 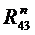^ 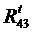и 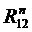^ 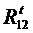. Точка f пересечения этих двух линий определит числовые значения и направления сил 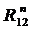, , 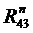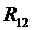и 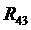. Полная реакция во внутреннем шарнире C двухповодковой группы определяется из условия равновесия сил, действующих на звенья 2 или 3:

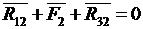
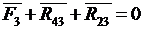
Соединяя точки b и f , найдем реакции .

Расчет ведущего (входного) звена. Это звено входит со стойкой во вращательную или поступательную пару пятого класса Кинематическая цепь статически определима при условии 3n -2p₅ = 0. Ведущее звено при n = 1 и p₅ = 1 не будет находиться в равновесии. Для того чтобы ведущее звено находилось в равновесии, необходимо дополнительно ввести уравновешивающую силу 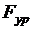или уравновешивающий момент 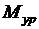, которые бы уравновесили все силы и моменты, приложенные к ведущему звену.

На рис.6 представлены два случая расчета реакции во вращательной паре пятого класса О

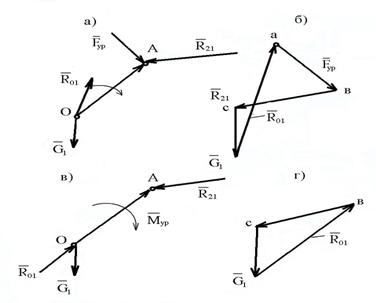
Рис.6. К кинетостатическому расчету ведущего звена:

а- силовое нагружение ведущего звена с уравновешивающей силой; б – план сил при наличие F_ур ; в – план сил при наличие М_ур; г – силовое нагружение с уравновешивающим моментом

В первом случае (рис.6,а) к ведущему звену приложена уравновешивающая сила F_ур, линией действия которой задана. Для ее определения составляем уравнение моментов всех сил, действующих на ведущее звено, относительно точки А:

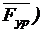M_A( + M_A( 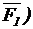+ M₁ + M_A( 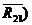= 0,

откуда

M_A( 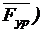= F_ур = -M[_A( 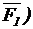+ M₁ + M_A( ],

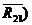или

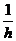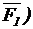F_ур = - [M_A( + M₁ + M_A( ].

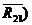Уравнение равновесия для ведущего звена

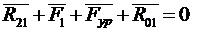
Реакция 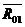определяется из плана сил (рис.6,б).

Во втором случае (рис.6,б) к ведущему звену приложен уравновешивающий момент M_ур. Из уравнения моментов относительно точки А определяем M_ур:

M_ур+ M_A( 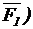+ M₁ + M_A( 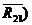= 0,

Откуда

M_ур = -[M_A( 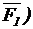+ M₁ + M_A( ].

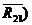Уравнение равновесия для ведущего звена в данном случае имеет вид

.

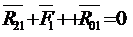Реакция 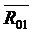определится из плана сил (рис.6д).

3.3. Трение в механизмах

Виды, характеристики. Силы трения скольжения и качения. Механический коэффициент полезного действия.

Трением называется сопротивление относительному перемещению соприкасающихся тел, возникающее в месте их соприкосновения. Трение представляет собой очень сложное явление. В соответствии с современной гипотезой, имеющей смешанный характер, процесс трения при скольжении поверхностей является результатом механического взаимодействия поверхностей и сил молекулярного сцепления.

В зависимости от характера относительного движения элементов кинематических пар, а также от характера соприкосновения тел внешнее трение может быть двух видов:

- трение скольжение, при котором одни и те же точки одного тела приходят в соприкосновение с различными точками другого тела;

- трение качение, при котором следующие одна за другой точки одного тела последовательно приходят в соприкосновение со следующими одна за другой точками другого тела.

В зависимости от состояния трущихся поверхностей различают трение скольжения следующих видов:

- сухое, возникающее при отсутствии смазки и загрязнений между поверхностями;

- граничное, получающееся в том случае, когда поверхности разделены слоем смазки толщиной не более 0,1 мкм;

- жидкостное, при котором поверхности полностью разделены слоем смазочного вещества;

- полусухое – смешанное трение – одновременно сухое и граничное;

- полужидкостное – одновременно жидкостное и граничное.

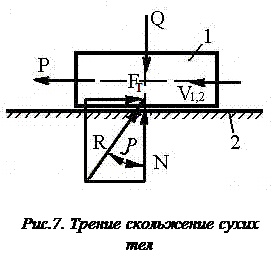
Основная зависимость между силой F_T, возникающей вследствие трения скольжения, и силой взаимодействия N тела 1 и 2 (рис.7) по нормали, установленная Амонтоном – Кулоном, имеет вид

F_T = f N,

где f – коэффициент трения, N = Q.

Коэффициент трения, являющийся. безразмерной величиной, зависит от физической природы и состояния трущейся пары, т.е.

шероховатости поверхности, наличия и сорта смазки, давления, скорости относительного скольжения и др. Опыты показали, что следует различать коэффициент трения покоя f_о ( при трогании с места или статического) от коэффициента трения движения (кинетического).

Из рис. 7 видно, что

tgr = 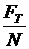= = 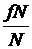f.

Полная реакция R отклонена от нормали N на угол r, который называют углом трения скольжения. Таким образом, для учета сил трения в поступательной паре реакцию R надо отклонить от направления нормали N так, чтобы она образовала тупой угол с вектором 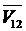относительной скорости ползуна 1 относительно направляющей 2.

Трение качения. Вследствие контактных деформаций трение качение сопровождается неизбежным скольжением и рассеиванием энергии в результате внутреннего трения. Для расчета силы трения используют формулу Амонтона – Кулона. При качении цилиндра по плоскости (рис.8)

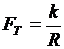F_n,

где k – коэффициент трения качения; R – радиус цилиндра ; F_n – сила, с которой цилиндр прижат к плоскости.

Коэффициент трения качения составляет k = (0,01…0,05)мм в зависимости от твердости стали.

Для уменьшения сил трения в зону соприкосновения (контакта) вводят смазочный материал. Действие смазочного материала, в результате которого уменьшается сила трения, называют смазкой.

Эффективность использования машин и механизмов оценивается их механическим коэффициентом полезного действия (КПД), который определяется отношением полезной работы ко всей совершенной работе

h = 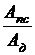= = 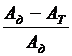1 - 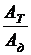= 1 - j,

где A_пс – работа сил полезного сопротивления;

A_д – работа движущих сил;

A_T – работа, связанная с преодолением сил трения в кинематических парах и сил сопротивления среды;

j =A_T/A_д - механический коэффициент потерь, который показывает, какая доля механической энергии, подведенной к машине, вследствие наличия различных видов трения превращается в конечном счете в теплоту и бесполезно теряется, рассеиваясь в окружающую среду. Так как потери неизбежны, то всегда j > 0. и, следовательно, всегда механический КПД h < 1.

Повышенные значения сил трения заметно снижают КПД механизма, существенно влияют на распределение сил и движения звеньев в механизме. При некоторых соотношениях между параметрами механизма вследствие трения движение звена в требуемом направлении невозможно независимо от величины движущей силы. Такое явление называется самоторможением механизма. В большинстве механизмов самоторможение недопустимо, но в некоторых случаях оно используется для предотвращения самопроизвольного движения в обратном направлении.

Лекция №4