Тема 1. Общие сведения о машинах и механизмах.

Теория механизмов и машин

Лекция №1

ВВЕДЕНИЕ

Теория механизмов и машин является одной из основных машиностроительных дисциплин. Она посвящена изучению наиболее общих вопросов исследования и проектирования механизмов и машин. К таким вопросам относятся:

1.Изучение строения (структуры) механизмов.

2.Определение положений механизмов и траекторий, описываемых отдельными точками.

3.Опредение скоростей и ускорений отдельных точек и звеньев механизма.

4.Исследование и проектирование различных механизмов.

5.Определение различных сил (внешних, реакций, трения, инерции), действующих на звенья механизма.

6.Изучение энергетического баланса машин (К.П.Д. и др.).

7.Изучения истинного закона движения машин под действием заданных сил.

8.Изучение способов регулирования скорости хода машин.

9.Изучение способов уравновешивания сил инерции в машинах.

В соответствии с этими вопросами теория механизмов и машин является наукой, изучающей строение, кинематику и динамику механизмов и машин.

Теория механизмов и машин привлекает для решения своих задач методы математики, физики и особенно теоретической механики, твердое знание которых необходимо для усвоения этого курса, и полностью используется при изучении дисциплины «Оборудование швейных предприятий». Содержание курса и порядок его изучения соответствуют Государственному образовательному стандарту «Теории механизмов и машин и рабочей программе Омского государственного института сервиса, составленной на кафедре естественнонаучных и инженерных дисциплин.

Тема 1. Общие сведения о машинах и механизмах.

Структура механизмов.

1.1. Основные понятия и определения

Машина. Классификация машин по их функциональному назначению. Звенья, их наименования по характеру движения. Кинематические пары, их классы и виды. Кинематические цепи, их виды Механизм, виды механизмов. Структурные формулы механизмов. Принцип образования механизмов. Структурные формулы. Класс и порядок механизма.

К основным понятиям данной темы курса относятся: машина, механизм, звено, кинематическая пара, кинематическая цепь.

Машина - это устройство, выполняющее механические движения для преобразования энергии, материалов и информации с целью замены или облегчения физического и умственного труда человека. В зависимости от основного функционального назначения различают: энергетические, технологические, транспортные и информационные машины. В энергетических машинах происходит преобразование энергии; в технологических - изменяются формы, размеры и состояние исходных материалов; с помощью транспортных машин происходит перемещение грузов, материалов, инструментов, людей и других объектов в пространстве с требуемой скоростью; в информационных машинах происходит преобразование вводимой информации для контроля, регулирования и управления технологическим процессом.

Механизмом называется устройство, предназначенное для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел.

Твердое тело, входящее в состав механизма, называется звеном. Звено может состоять из одной или нескольких неподвижно соединенных деталей, движущихся как одно целое.

Подвижное соединение двух соприкасающихся звеньев называется кинематической парой. Кинематические пары различают по характеру соприкосновения звеньев: пару называют низшей, если элементы звеньев соприкасаются по поверхности, и высшей, если только по линиям или в точках. Одно из преимуществ низших пар по сравнению с высшими – возможность передачи больших сил, поскольку контактная поверхность соприкасающихся звеньев низшей пары может быть весьма значительна. Применение высших пар позволяет уменьшить трение в машинах и получать нужные, самые разнообразные законы движения выходного звена механизма путем придания определенной формы звеньям, образующих высшую пару.

Кинематические пары классифицируют по числу условий связи S (по числу ограничений, накладываемых кинематической парой на относительные движения звеньев, образующих данную кинематическую пару). По значению S определяют класс кинематической пары. При S=0 пары не существует, а имеются два тела, движущихся независимо друг от друга; при S=6 кинематическая пара превращается в жесткое соединение двух деталей. Чаще всего в механизмах встречаются вращательные и поступательные кинематические пары 5-го класса

Совокупность звеньев, образующих между собой кинематические пары, называется кинематической цепью. Различают замкнутые и незамкнутые, плоские и пространственные кинематические цепи. В каждом механизме есть одно неподвижное (или принимаемое за неподвижное) звено, называемое стойкой. Различают входные и выходные звенья механизма. Входным называют звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Выходным называют звено, совершающее движение, для выполнения которого предназначен механизм. По характеру движения звенья называют: кривошип – вращающееся звено рычажного механизма, которое может совершать полный оборот вокруг неподвижной оси; коромысло – вращающееся звено рычажного механизма, которое может совершать только неполный оборот вокруг неподвижной оси; шатун – звено рычажного механизма, образующего кинематические пары только с подвижными звеньями; ползун – звено рычажного механизма, образующего поступательную пару со стойкой; кулиса – звено рычажного механизма, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару.

Механизмы делятся на плоские и пространственные. Плоским называется механизм, точки звеньев которого движутся в одной или параллельных плоскостях.

К основным видам механизмов относятся: рычажные, кулачковые, зубчатые, фрикционные, цепные, ременные, гидравлические, пневматические и волновые.

Рычажными называют механизмы, в состав которых входят только низшие кинематические пары. Эти механизмы могут обеспечивать передачу значительных сил, т.к. в этих кинематических парах звенья соприкасаются по поверхностям. В виду ограниченного числа видов низших кинематических пар многие важные законы преобразования движения звеньев не могут быть получены с помощью рычажных механизмов. В этом плане большими возможностями обладают механизмы с высшими парами, которые, однако, менее износостойкие, чем низшие.

В системах управления широко применяются кулачковые механизмы. Кулачок – это звено, которому принадлежит элемент высшей пары. Разнообразие форм, которые можно придать кулачку, определяют большое разнообразие возможных преобразований движения. Одна из особенностей кулачковых механизмов состоит в том, что может быть обеспечено движение выходного звена с остановками за конечный промежуток времени при непрерывном движении входного.

Для передачи вращательного движения с изменением угловой скорости используются зубчатые, червячные, фрикционные, ременные и цепные передачи. В зубчатых механизмах передача вращательного движения происходит за счет взаимодействия зубьев (выступов) зацепляющихся колес. Во фрикционных механизмах передача вращательного движения происходит за счет сил трения, возникающих между соприкасающихся звеньев. В цепных и ременных передачах вращающиеся звенья соединяются соответственно с помощью цепей или ремней. Эти передачи используются при значительных расстояниях между осями вращающихся звеньев. В гидравлических механизмах преобразование движения происходит посредством твердых и жидких тел, а в пневматических - с помощью твердых и газообразных. Действие волновых передач основано на деформации отдельных звеньев. С помощью этих передач вращательное движение может быть передано через герметичную стенку.

При изображении механизма на чертеже различают его структурную (принципиальную) схему с применением условных обозначений звеньев и пар (без указания размеров звеньев) и кинематическую схему с размерами, необходимыми для кинематического расчета. На схемах звенья обозначают цифрами, а пары и различные точки звеньев – большими буквами латинского алфавита.

Структура механизмов

Лекция №2

Задачи и методы

Рычажные механизмы используются в качестве передаточных механизмов, воспроизводящих заданную функциональную зависимость между перемещениями входных и выходных звеньев. Они часто используются также и для перемещения некоторого объекта из одного положения в другое. Механизмы, в состав которых входят только вращательные пары, называются шарнирными. Если в шарнирном четырехзвенном механизме заменить одну или две вращательные пары на поступательные, то можно получить: кривошипно-ползунный механизм, кулисный, синусный, механизм эллипсографа.

Задачами кинематического анализа рычажных механизмов являются: определение положений звеньев механизма; траекторий отдельных точек звеньев механизма; скоростей и ускорений точек звеньев механизма; угловых скоростей и ускорений звеньев.

Для решения этих задач используются аналитические, графоаналитические, графические и экспериментальные методы исследования. Задача об аналитическом определении скоростей и ускорений решается дифференцированием по времени уравнений для определения положений звеньев, что приводит к системе линейных уравнений относительно искомых величин. Более просто, однако с меньшей точностью, задачи кинематического анализа решаются графическим способом. Положения звеньев механизма находятся с помощью простейших графических построений. Скорости и ускорения определяются с помощью кинематических диаграмм, полученных графическим дифференцированием диаграммы перемещения заданной точки звена.

Достаточно простым и вместе с тем достаточно точным и наглядным является графоаналитический метод (метод планов скоростей и ускорений). Он основан на графическом решении векторных уравнений, составленных для определения искомых скоростей и ускорений. Составление векторных уравнений связано с использованием уравнений двух типов: одного - связывающего скорости (ускорения) двух точек, принадлежащих одному звену, и второго - связывающего скорости (ускорения) двух точек, совпадающих в данный момент, но принадлежащих разным звеньям поступательной пары.

Графоаналитический метод

На практике широко применяют метод планов скоростей и ускорений. Метод основан на графическом решении векторных уравнений движения. Для построения планов скоростей и ускорений механизма должна быть известна его кинематическая схема и задан закон движения входного звена.

В качестве примера рассмотрим кинематику кривошипно-коромыслового механизма (механизма игловодителя швейной машины) (рис.4).

Для заданного положения механизма известны угловые скорости и ускорения входного звена. Для простоты решения задачи будем полагать, что угловое ускорение входного звена равно нулю.

Построение плана скоростей начинается с определения скорости точка А кривошипа

V_A = ω∙l_OA (4)

Вектор скорости V_A направлен перпендикулярно кривошипу ОА в направлении его вращения (угловой скорости). Точка В, принадлежащая звену 2, рассматривается в относительном движении вокруг точки А. Скорость точки В можно представить как векторную сумму скоростей переносного и относительного движений. Переносным движением будем считать скорость точки А, а относительным – вращательное движение звена 2 вокруг точки А .Обозначая последнюю через V_ВА, получаем следующее уравнение для скорости точки В:

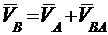, (5)

где 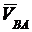^ BA, и // ОВ.

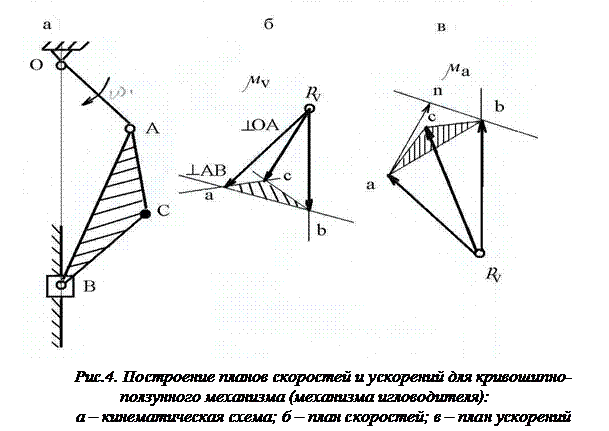Для определения указанных неизвестных величин строим план скоростей в выбранном масштабе скорости m_v. Из произвольного полюса p_v (рис.4,б) проводим вектор р_vа =V_A/m_v, перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости V_A. Из конца вектора р_vа (точка а) проводим линию в направлении относительной скорости 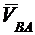, перпендикулярную АВ, а из полюса p_v – линию в направлении скорости V_B, параллельную ОВ В пересечении указанных линий находим точку b. Вектор р_vb изображает скорость 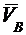точки В, а вектор ab – скорость 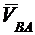. Значения действительных скоростей находим по формулам:

V_B = m_v∙ р_vb и

V_BA = m_v∙ ab

Для определения скорости точки С шатуна можно воспользоваться известной из теоретической механики теоремой подобия для скоростей, согласно которой отрезки прямых линий, соединяющие точки на схеме звена механизма и отрезки прямых линий, соединяющие концы векторов относительных скоростей этих точек на плане скоростей, образуют подобные фигуры. Фигура на плане скоростей повернута относительно фигуры схемы звена на 90° (свойство планов скоростей).

Вектор р_vс скорости точки С находим построением на отрезке ab треугольника abc , подобного треугольнику ABC, повернутому на 90°. Для этого из точки а плана скоростей проводим линию, перпендикулярную АС, а через точку b – перпендикулярную ВС. Значение скорости в этой точке вычисляем по формуле

V_C= m_v∙р_vс

Угловая скорость звена 2

w₂ = V_BA/l_BA

Направление w₂ находится по вектору скорости V_BA.

Планы скоростей механизмов позволяют охарактеризовать движение механизма:

– векторы, выходящие из полюса плана скоростей (р_v) , представляют собой абсолютные скорости;

– вектор, соединяющий концы абсолютных скоростей, представляют собой относительную скорость; он направлен к той точке, которая стоит первой в индексе скорости;

– план скоростей дает возможность находить касательные к траекториям точек механизма, не выстраивая этих траекторий;

– полюс плана скоростей (р_v) соответствует мгновенному центру вращения звена (МЦВ).

Построение плана ускорений начинают с построения абсолютного ускорения a_A точки А кривошипа, складывающегося геометрически из суммы нормальной (a_Aⁿ = w₁²∙l_OA) тангенциальной (a_A^t = e₁∙l_OA) составляющих:

a_A = a_Aⁿ + a_A^t .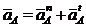

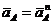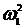
При = 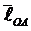Выбрав масштаб плана ускорений m_a, из произвольной точки p_a (рис.4в), называемой полюсом плана ускорений, откладываем ускорение a_Aⁿ в виде вектора p_aа, направленного от точки А к точке О (рис.4а)

Ускорение точки В находим из уравнения

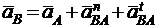
Значение нормальной составляющей относительного ускорения определяется по формуле

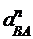= w₂²∙l_AВ

Вектор 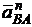направлен по АВ к центру вращения (к точке А механизма) и откладывается из точки а плана. В виде отрезка an = 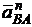/m_a. Направление тангенциальной составляющей вектора 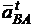будет проходить через конец n вектора 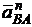и перпендикулярно к нему. Направление абсолютного ускорения точки В известно (а_В //ОВ) и соответствующая линия проходит через полюс р_а.. Пересечение этих двух линий определит положение точки b на плане ускорений, а следовательно, величину ускорения а_В = m_a∙р_аb. Вектор ab изображает полное ускорение 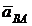. Угловое ускорение звена 2 находим по формуле

e₂∙= a^t_ВА/l_AВ.

Перенося вектор ускорения 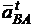в точку В и рассматривая движение точки В относительно точки А, находим направление e₂.

Вектор р_ас ускорения точки С находим, используя свойство плана ускорений, построением на отрезке ab треугольника abc, подобного треугольнику АВС, повернутого на угол (180° - a), где

a = arctge₂/w₂²

Значение ускорения в этой точке равно а_C = m_a∙р_аc.

План ускорений имеет следующие характеристики:

· векторы, выходящие из полюса р_а плана ускорений, представляют собой абсолютные ускорения соответствующих точек звеньев механизма;

· отрезки, расположенные между концами векторов абсолютных ускорений, соответствуют полным относительным ускорениям;

· концы векторов абсолютных ускорений точек, принадлежащих одному звену механизма, на плане ускорений образуют подобные фигуры, повернутые на угол (180° - a);

· план ускорений позволяет находить угловые ускорения звеньев.

Лекция №3

Силы, действующие в машинах

Развитое машинное устройство, состоящее из двигателя, передаточных механизмов и рабочей машины и, в некоторых случаях, контрольно-управляющих машин, называется машинным агрегатом. К механизмам машинного агрегата во время его движения приложены различные силы. В зависимости от знака элементарной работы все эти силы подразделяются на силы движущие F_д (М _д ) и силы сопротивленияF _с (M_с), силы тяжести G и инерционные силы F_и (M_и), силы взаимодействия между k-тым и i-тым звеньями механизмов т.е. силы, действующие в кинематических парах (реакции в кинематических парах R_ki). Движущей силой называется сила, элементарная работа которой положительна, а силой сопротивления - сила элементарная работа которой отрицательна. Элементарная работа силы определяется как скалярное произведение силы на элементарное перемещения точки ее приложения. Силы сопротивления в свою очередь делятся на силы F_пс (или моменты сил M_пс) полезного сопротивления (силы, для преодоления которых предназначена данная машина) и силы F_вс (или моменты сил M_вс) вредного сопротивления(силы трения и силы сопротивления окружающей среды). Для определения силы трения рекомендуется использовать формулу Амонтона-Кулона. Силы тяжести G могут быть или силами движущими, или силами сопротивления в зависимости от направления перемещения центра тяжести звена.

Инерционные силы F_и и их моменты M_и определяются по известным из теоретической механике формулам:

F_и = -m×a_s,

M_и = - I_s×e,

где m – масса звена, кг;

a_s – ускорение центра масс звена, м/с²;

I_s – момент инерции звена относительно оси, проходящей че-

рез его центр масс перпендикулярно к плоскости движения, кг×м²;

e - угловое ускорение звена, с^-2.

Методы динамического анализа (исследования) в данном курсе рассматриваютсяприменительно к плоским механизмам с одной степенью свободы, которые являются наиболее распространенными. Одной из задач динамического анализа механизма является проведение кинетостатического (силового) расчета, при котором определяются реакции в кинематических парах и уравновешивающий момент (уравновешивающая сила), приложенный к исходному механизму от действия внешних сил и сил инерции.

Силовой расчет ведется с использованием принципа д'Аламбера методом планов сил по отдельным структурным группам Ассура, представляющих собой кинетостатически определимые системы (кинематические цепи). Для этих цепей число неизвестных реакций в кинематических парах равно числу условий кинетостатики. Знание реакций в кинематических парах необходимо для расчета звеньев механизма на прочность. Уравновешивающий момент обеспечивает заданный закон движения входного звена, а, следовательно, и всего механизма. Для технологических машин по уравновешивающему (движущему) моменту и частоте вращения входного звена определяется мощность приводного двигателя.

Силовой расчет

Силовой расчет начинается с последней, т.е. наиболее удаленной от ведущего звена группы Ассура, и кончается расчетом ведущего звена.

В качестве примера рассмотрим силовой расчет двухповодковой групп Ассура. На рис.5,а приведена схема двухповодковой группы второго класса первого вида. На звенья 2 и 3 действуют известные силы и моменты. В точках B и D прикладываем неизвестные реакции R₁₂ и R₄₃ отброшенных звеньев 1 и 4 на оставшиеся 2 и 3, условно направляя их вверх. Уравнение равновесия группы имеет вид

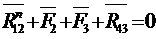
Разложим векторы реакций на составляющие по направлениям звеньев (нормальные) и перпендикулярно звеньям (тангенциальные):

; .

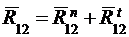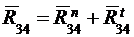Тогда уравнение равновесия примет вид

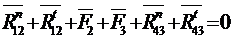
Составляющие реакци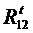и и 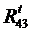определяют из условия равновесия звеньев 2 и 3. Для этого составляют уравнения моментов для каждого из звеньев относительно точки C.

Для звена 2

M_C( 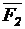) + M_C( 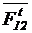) + M₂ = 0,

откуда

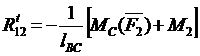
Для звена 3

M_C( 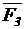) + M_C( 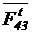) + M₃ = 0,

откуда

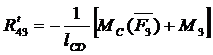
Составляющие реакци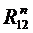й и 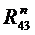и полные реакци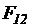и и 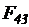определяем из плана сил (рис.5б), построенного на основе уравнения равновесия.

Из начала плана сил (точка а) в некотором масштабе m_F проводим вектор силы 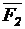и из его конца – вектор силы 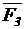.Из начала вектора 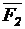и из конца вектора 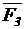проводим найденные выше силы 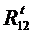^BC и 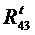^CD. Из точек d и e проводим линии в направлении сил 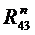^ 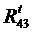и 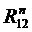^ 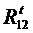. Точка f пересечения этих двух линий определит числовые значения и направления сил 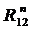, , 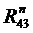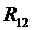и 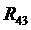. Полная реакция во внутреннем шарнире C двухповодковой группы определяется из условия равновесия сил, действующих на звенья 2 или 3:

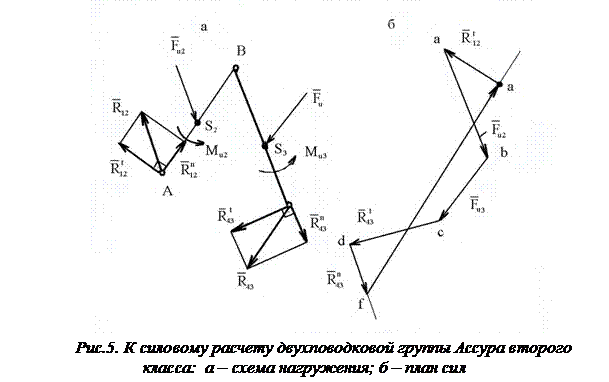
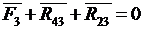
Соединяя точки b и f , найдем реакции .

Расчет ведущего (входного) звена. Это звено входит со стойкой во вращательную или поступательную пару пятого класса Кинематическая цепь статически определима при условии 3n -2p₅ = 0. Ведущее звено при n = 1 и p₅ = 1 не будет находиться в равновесии. Для того чтобы ведущее звено находилось в равновесии, необходимо дополнительно ввести уравновешивающую силу 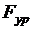или уравновешивающий момент , которые бы уравновесили все силы и моменты, приложенные к ведущему звену.

На рис.6 представлены два случая расчета реакции во вращательной паре пятого класса О

Рис.6. К кинетостатическому расчету ведущего звена:

а- силовое нагружение ведущего звена с уравновешивающей силой; б – план сил при наличие F_ур ; в – план сил при наличие М_ур; г – силовое нагружение с уравновешивающим моментом

В первом случае (рис.6,а) к ведущему звену приложена уравновешивающая сила F_ур, линией действия которой задана. Для ее определения составляем уравнение моментов всех сил, действующих на ведущее звено, относительно точки А:

M_A( + M_A( 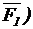+ M₁ + M_A( 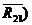= 0,

откуда

M_A( 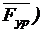= F_ур = -M[_A( 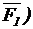+ M₁ + M_A( ],

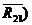или

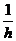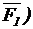F_ур = - [M_A( + M₁ + M_A( ].

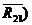Уравнение равновесия для ведущего звена

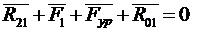
Реакция 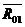определяется из плана сил (рис.6,б).

Во втором случае (рис.6,б) к ведущему звену приложен уравновешивающий момент M_ур. Из уравнения моментов относительно точки А определяем M_ур:

M_ур+ M_A( 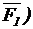+ M₁ + M_A( 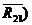= 0,

Откуда

M_ур = -[M_A( 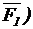+ M₁ + M_A( ].

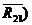Уравнение равновесия для ведущего звена в данном случае имеет вид

.

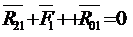Реакция 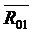определится из плана сил (рис.6д).

3.3. Трение в механизмах

Виды, характеристики. Силы трения скольжения и качения. Механический коэффициент полезного действия.

Трением называется сопротивление относительному перемещению соприкасающихся тел, возникающее в месте их соприкосновения. Трение представляет собой очень сложное явление. В соответствии с современной гипотезой, имеющей смешанный характер, процесс трения при скольжении поверхностей является результатом механического взаимодействия поверхностей и сил молекулярного сцепления.

В зависимости от характера относительного движения элементов кинематических пар, а также от характера соприкосновения тел внешнее трение может быть двух видов:

- трение скольжение, при котором одни и те же точки одного тела приходят в соприкосновение с различными точками другого тела;

- трение качение, при котором следующие одна за другой точки одного тела последовательно приходят в соприкосновение со следующими одна за другой точками другого тела.

В зависимости от состояния трущихся поверхностей различают трение скольжения следующих видов:

- сухое, возникающее при отсутствии смазки и загрязнений между поверхностями;

- граничное, получающееся в том случае, когда поверхности разделены слоем смазки толщиной не более 0,1 мкм;

- жидкостное, при котором поверхности полностью разделены слоем смазочного вещества;

- полусухое – смешанное трение – одновременно сухое и граничное;

- полужидкостное – одновременно жидкостное и граничное.

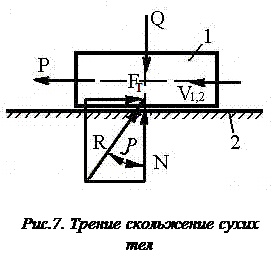
Основная зависимость между силой F_T, возникающей вследствие трения скольжения, и силой взаимодействия N тела 1 и 2 (рис.7) по нормали, установленная Амонтоном – Кулоном, имеет вид

F_T = f N,

где f – коэффициент трения, N = Q.

Коэффициент трения, являющийся. безразмерной величиной, зависит от физической природы и состояния трущейся пары, т.е.

шероховатости поверхности, наличия и сорта смазки, давления, скорости относительного скольжения и др. Опыты показали, что следует различать коэффициент трения покоя f_о ( при трогании с места или статического) от коэффициента трения движения (кинетического).

Из рис. 7 видно, что

tgr = 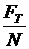= = 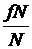f.

Полная реакция R отклонена от нормали N на угол r, который называют углом трения скольжения. Таким образом, для учета сил трения в поступательной паре реакцию R надо отклонить от направления нормали N так, чтобы она образовала тупой угол с вектором 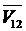относительной скорости ползуна 1 относительно направляющей 2.

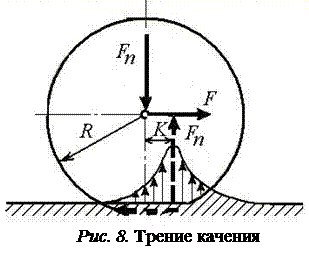
Трение качения. Вследствие контактных деформаций трение качение сопровождается неизбежным скольжением и рассеиванием энергии в результате внутреннего трения. Для расчета силы трения используют формулу Амонтона – Кулона. При качении цилиндра по плоскости (рис.8)

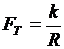F_n,

где k – коэффициент трения качения; R – радиус цилиндра ; F_n – сила, с которой цилиндр прижат к плоскости.

Коэффициент трения качения составляет k = (0,01…0,05)мм в зависимости от твердости стали.

Для уменьшения сил трения в зону соприкосновения (контакта) вводят смазочный материал. Действие смазочного материала, в результате которого уменьшается сила трения, называют смазкой.

Эффективность использования машин и механизмов оценивается их механическим коэффициентом полезного действия (КПД), который определяется отношением полезной работы ко всей совершенной работе

h = 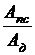= = 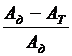1 - 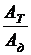= 1 - j,

где A_пс – работа сил полезного сопротивления;

A_д – работа движущих сил;

A_T – работа, связанная с преодолением сил трения в кинематических парах и сил сопротивления среды;

j =A_T/A_д - механический коэффициент потерь, который показывает, какая доля механической энергии, подведенной к машине, вследствие наличия различных видов трения превращается в конечном счете в теплоту и бесполезно теряется, рассеиваясь в окружающую среду. Так как потери неизбежны, то всегда j > 0. и, следовательно, всегда механический КПД h < 1.

Повышенные значения сил трения заметно снижают КПД механизма, существенно влияют на распределение сил и движения звеньев в механизме. При некоторых соотношениях между параметрами механизма вследствие трения движение звена в требуемом направлении невозможно независимо от величины движущей силы. Такое явление называется самоторможением механизма. В большинстве механизмов самоторможение недопустимо, но в некоторых случаях оно используется для предотвращения самопроизвольного движения в обратном направлении.

Лекция №4

Задачи уравновешивания

При движении механизма различные точки его звеньев движутся с ускорениями, в результате чего возникают силы инерции, которые вызывают дополнительные нагрузки в кинематических парах. Эти нагрузки, которые могут в десятки раз превосходить статические, изменяясь по величине и по направлению, передаются раме и фундаменту и вызывают их вибрацию, колебания и расшатывание. Кроме того, они деформируют валы и дополнительно нагружают подшипники, ускоряя их износ. Особенно велики силы инерции и вызываемые ими нагрузки в современных быстроходных машинах. Отсюда возникает задача о проектировании машин таким образом, чтобы избежать (полностью или частично) указанные нагрузки.

Различают две задачи:

- уравновешивание вращающихся звеньев (роторов);

- уравновешивание машин на фундаменте.

Балансировка роторов

Правильно спроектированные с точки зрения уравновешенности звенья все же вследствие неоднородности материала, точности изготовления, дефектов сборки могут оказаться на практике несколько неуравновешенными. Дисбаланс таких звеньев должен быть обнаружен и устранен.

Процесс устранения неуравновешенности звеньев называется балансировкой. Балансировка бывает статической и динамической.

Статическая балансировка применяется для деталей, имеющих небольшие относительно размеры вдоль оси вращения. Осуществляется она чаще всего на балансировочных параллелях 1 (рис.9)

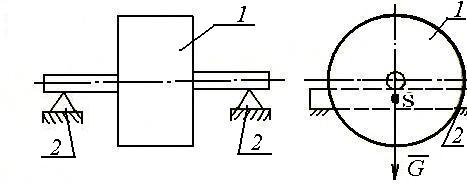
Рис.9. Схема установки для статической балансировки

Статическая неуравновешенность – несовпадение центра масс звена с осью вращения – может быть обнаружена простыми приспособлениями при нахождении звена в покое. Если положить статически неуравновешенное звено (ротор) своей осью вращения на горизонтальные призмы (рис.9),то звено будет перекатываться на призмах до тех пор, пока центр масс звена не займет нижнее положение, т.е. будет расположен внизу на вертикали, проходящей через ось вращения. Располагая уравновешивающую массу по этой же вертикали вверху (для этого можно применить , например, пластилин или другую какую-либо мастику), при помощи ряда попыток устанавливают величину этой массы. Попытки проводятся до тех пор, пока звено не будет занимать положение безразличного равновесия. Затем уравнове