Построение D-оптимальных моделей пространства состояний

ПРОЦЕДУРА ПОСЛЕДОВАТЕЛЬНОЙ D-ОПТИМАЛЬНОЙ ИДЕНТИФИКАЦИИ (ДППИ).

Зададим линейно-комбинационную модель следующим образом :

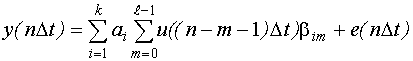
Задача сводится к нахождению вектора 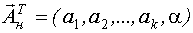, а точнее его оптимального значения и его ковариационной матрицы.

Поскольку модель нелинейно-параметризованная, будем опираться на теорию последовательного планирования эксперимента, а именно на D-оптимальную процедуру последовательной идентификации (ДППИ).

D-оптимальная процедура последовательной идентификации может быть сформулирована следующим образом: объект исследования возбуждается в момент времени 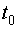путем подачи на его вход некоторого "затравочного" тестирующего сигнала протяженностью 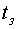. Затравочный тестирующий сигнал должен обеспечивать возможность оценивания элементов вектора 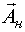, причем при оценке опираемся на теорию нелинейного оценивания статических моделей.

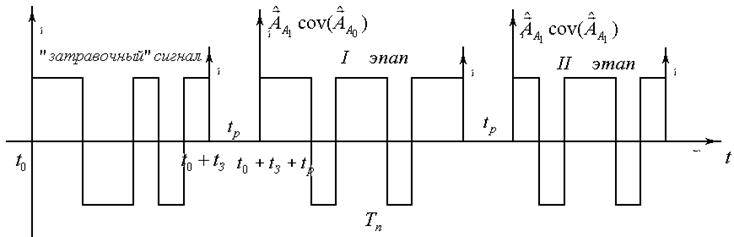
Начиная с момента времени ( 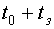) в течение времени 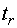вычисляются оценки элементов вектора 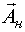и синтезируется первичный участок локального D-оптимального тестирующего сигнала. С момента времени 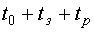. Протяженность участка после 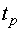будет либо равна 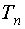, если производится планирование одного измерения, либо больше 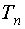, если производится планирование более одного измерения.

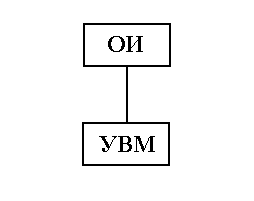
После окончания реализации первого участка сигнала и проведения всех запланированных измерений выхода необходимо уточнить НМНК оценки вектора 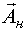и синтезировать второй участок локального D-оптимального плана, проверив перед этим правило останова ДППИ. Уточнение производится с учетом всех ранее произведенных измерений выхода, включая измерения этапа затравочного тестирования.

После синтеза второго участка сигнала он подается на вход объекта, и процедура повторяется вплоть до выполнения правила останова. Правило останова ДППИ то же, что и для моделей статики. Таким образом, в процессе реализации в реальном времени осуществляется синтез участков локального D-оптимального тестирующего сигнала и поэтапное уточнение НМНК оценок параметров модели. По окончании ДППИ получается близкая к D-оптимальной нелинейно-параметризованная динамическая регрессионная модель.

В результате эксперимента имеем неоптимальные участки ( 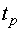). Для обеспечения непрерывности сигнала необходимо заполнить эти неоптимальные интервалы длительностью 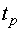каждый. Возможно несколько подходов.

I подход применим, если время расчета меньше шага дискретизации ( 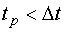)., Тогда, если симметричные участки локального D-оптимального тестирующего сигнала эквивалентны, то на вход объектов в течение интервалов 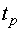можно подавать сигнал либо верхнего, либо нижнего уровня, если синтезируемый сигнал двухуровневый. Однако предварительно нужно доказать двухуровневость сигнала и эквивалентность его симметричных участков.

При этом обеспечивается сокращение длины сигнала на 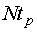, где N - общее число реализованных этапов за счет исключения из реализации участков расчета планирование каждого этапа. То есть уточнение оценок и синтез каждого участка сигнала производится параллельно с тестированием объекта в начале реализации планируемого этапа.

II подход применим, если время расчета больше шага дискретизации ( 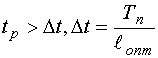). При этом непрерывность тестирующего сигнала может быть обеспечен, если планирование каждого этапа ДППИ производить в конце реализации предыдущего этапа, и использовать при этом прогнозируемое значение вектора НМНК оценок к моменту окончания реализации предыдущего этапа. В этом случае планирование каждого этапа осуществляется в конце реализации предыдущего в отличие от первого подхода, когда планирование осуществляется в начале следующего этапа. В данном случае сигнал хуже, так как предполагает планирование не строго локальных D-оптимальных участков из-за замены НМНК оценоких прогнозируемыми значениями.

ОСОБЕННОСТИ РЕАЛИЗАЦИИ ДППИ.

Вычисление начальной оценки 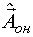по результатам затравочного тестирования производится по методике пассивного эксперимента методом Гаусса-Ньютона. Начальное приближение определяется из предположения, что  известно.

Планирование этапов осуществляется путем решения следующей аргументной задачи:

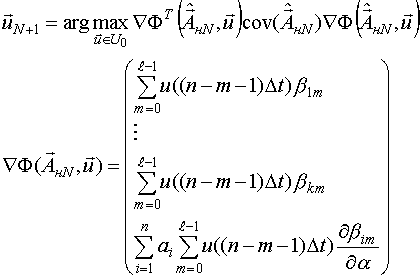
При планировании эксперимента в задачах нелинейного оценивания нормирование факторов не производится, поэтому в данной задаче пространство планирования определяется следующей системой неравенств:

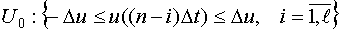
При этом предполагается, что: ,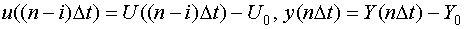

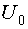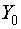где и - значения входа и выхода объекта в исходном статическом состояни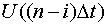и;

и 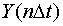- истинные дискретные значения входа и выхода;

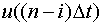и 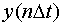- отклонения.

Для того, чтобы решить задачу проанализируем дисперсионную функцию:

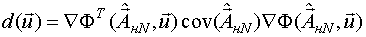
Покажем, что квадратичная форма относительно вектора является квадратичной формой относительно вектора факторов планирования.

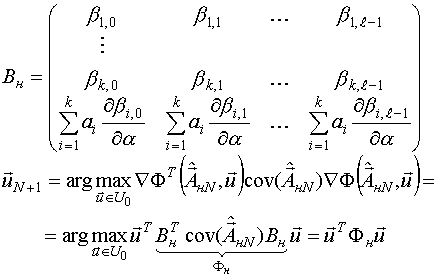
Таким образом, участки локальных D-оптимальных тестирующих сигналов для линейно-комбинационной модели являются двухуровневыми ( 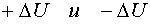), а симметричные участки сигнала эквивалентны.

Эти свойства позволяют обеспечить непрерывность синтезируемого D-оптимального тестирующего сигнала ( за счет того, что мы можем подавать произвольный сигнал 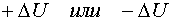), а также упростить задачу склеивания участков сигнала.

Известна теорема, что участки локального D-оптимального тестирующего сигнала, предполагающие одно измерение выхода, имеют не более k переключений, то есть при синтезе такого участка сигнала достаточно просмотреть лишь те вершины пространства 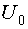, которым соответствуют участки сигнала, имеющие не более k переключений. Эта теорема позволяет ускорить планирование этапов ДППИ.

Рассмотрим II случай, когда время расчета больше шага дискретизации ( 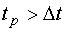). В этом случае синтез очередного участка сигнала производится с использованием прогнозируемых значений НМНК оценок элементов вектора неизвестных коэффициентов .

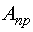Рассмотрим задачу планирования n+1 этапа ДППИ на основе оценки .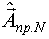

Прогнозирование НМНК-оценок неизвестных параметров

Прогнозирование возможно, если на каждом этапе процедуры производится несколько запланированных измерений выхода. Синтез участка, предполагающего несколько измерений выхода, производится по следующему алгоритму:

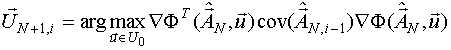
где 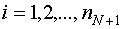- порядковый номер синтезируемого участка сигнала;

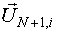- i-тая точка плана, которая должна быть реализована на (N+1) этапе процедуры. Эта точка определяет i-тый участок сигнала, определяющий предысторию для i-того измерения выхода (N+1) этапа;

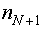- число планируемых измерений;

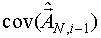- ковариационная матрица вектора 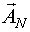, если его

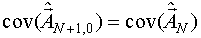
Для формализации данной процедуры необходимо получить рекуррентное выражение, связывающее ковариационную матрицу 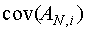c ковариационной матрицей 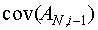для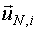

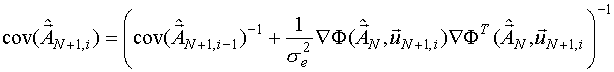
Для получения рекуррентной формулы можно воспользоваться известной теоремой из матричной алгебры: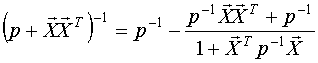

Тогда получим:

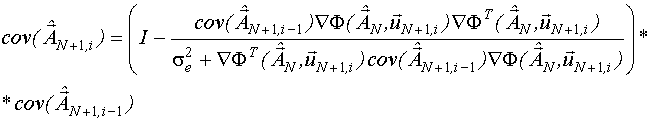
Искомая рекуррентная процедура синтеза участков локального D-оптимального тестирующего сигнала (N+1) этапа, предполагающего 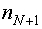измерение определяется следующими матричными выражениями:

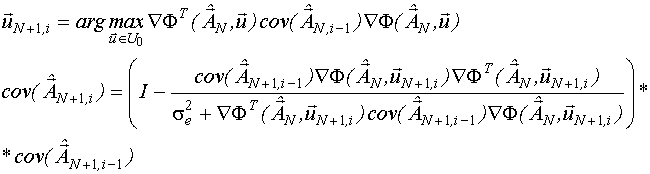где .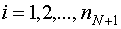

Прогнозирование оценок неизвестных параметров производится на интервале времени между 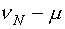и 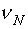измерениями выхода N-ого этапа ДППИ.

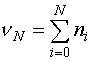
Если интервал между 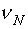и 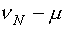измерениями больше 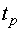, то можно производить прогнозирование. При этом предполагается, что интервал между этими измерениями не меньше .

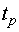Оценка 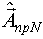, то есть прогнозирование вектора 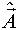к моменту реализации N-ого этапа вычисляется из следующего условия:

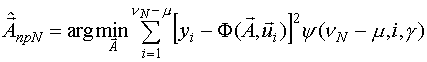- это критерий взвешенного МНК.

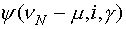- функция веса;

- параметр функции веса.

Функция веса вводится для того, чтобы уменьшить влияние на прогноз старых измерений, то есть измерений, удаленных от момента прогнозирования. Обычно функция веса записывается в виде:

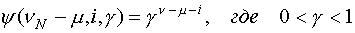
Параметр  априори неизвестен и должен оцениваться на каждом этапе процедур. Оценка коэффициента  находится из условия:

,

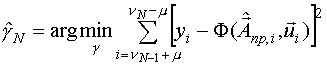где 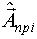- прогнозируемое значение оценок к моменту i-того измерения выхода.

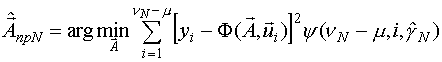
Можно показать, что оценка вычисляется с помощью следующей рекуррентной процедуры, которая является взвешенным НМНК:

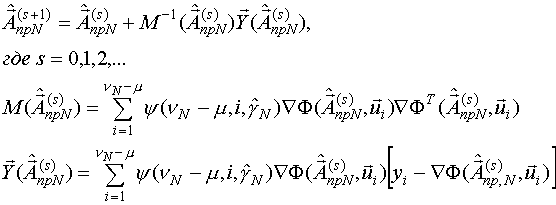
ОСОБЕННОСТИ СИНТЕЗА
НЕЛИНЕЙНЫХ D-ОПТИМАЛЬНЫХ МОДЕЛЕЙ ДИНАМИКИ.

Построение D-оптимальных нелинейных моделей осуществляется на основе ДППИ аналогично процедуре, рассмотренной для моделей линейных систем.

При реализации данной процедуры необходимо учитывать следующие особенности, присущие нелинейным системам:

1)Для нелинейных систем не выполняется принцип суперпозиции (принцип суперпозиции - когда выходной сигнал объекта равен сумме реакций всех входных сигналов), поэтому модели таких систем связывают не отклонения значения входа и выхода от исходного статистического состояния, а истинного значения входа-выхода. Таким образом, производство планирования для нелинейных систем может быть задано системой неравенств:

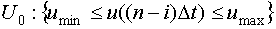
2) Участки локального D-оптимального тестирующего сигнала для нелинейных систем не являются двухуровневыми, поскольку ни одна из соответствующих им дисперсионных функций не может быть представлена в виде квадратичной формы относительно вектора .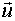

Например, для модели Винера:

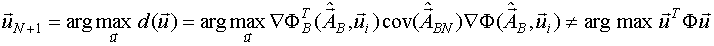
Таким образом, локальные D-оптимальные тестирующие сигналы для нелинейных систем являются многоуровневыми, причем число уровней априори неизвестно.

При анализе участков сигнала в общем случае необходимо просмотреть все пространство планирования 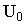, что резко усложняет задачу планирования участков ДППИ.

На практике обычно задают три уровня сигнала: 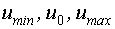и синтезируется сигнал в классе трехуровневых сигналов:

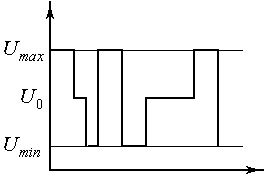
Пространство в этом случае будет квадратом, кубом, гиперкубом и так далее, так как для каждого сигнала ограничительные условия одинаковые.

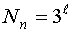
3) Поскольку число уровней априори неизвестно, симметричные участки не эквивалентны, то планирование этапов ДППИ должно всегда производиться в конце реализации предыдущего этапа на основе прогнозируемых значений оценок.

ПОСТРОНИЕ D-ОПТИМАЛЬНЫХ МОДЕЛЕЙ ПРОСТРАНСТВА СОСТОЯНИЙ.

Рассмотрим модель пространства состояний:

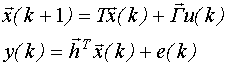
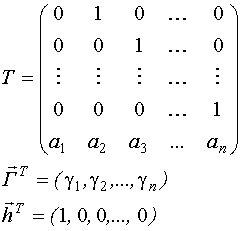
При нулевых начальных условиях перейдем к модели типа "вход-выход":

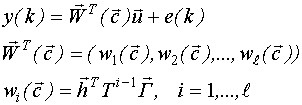
Планирование этапов ДППИ для моделей пространства состояний производится путем решения аргументной задачи: 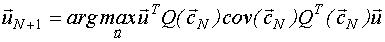, полученной из выражения:

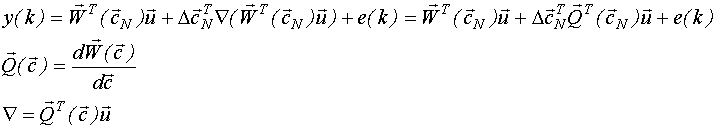
Мы получили модель, представленную в виде ряда Тейлора :

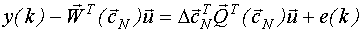
Пространство планирования 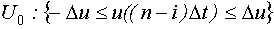, так как объект линейный.

Поскольку максимизированная квадратичная форма является квадратичной формой относительно вектора U, синтезируемые участки локального D-оптимального тестирующего сигнала для этой модели являются двухуровневыми, а симметричные участки эквивалентны.

Известна теорема, согласно которой синтезируемые участки сигнала имеют не более 2n-1 переключений.

При построении непрерывного тестирующего сигнала на основе точек плана можно использовать те же два подхода, что и для моделей типа "вход-выход".

Тема 17. Планирование эксперимента в условиях неоднородностей