Назначение дробного факторного эксперимента

Полуреплики

Четвертьреплики

НАЗНАЧЕНИЕ ДРОБНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА

Дробный факторный эксперимент предназначен для построения тех же моделей, что и полный факторный эксперимент:

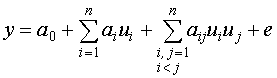
При дробном факторном эксперименте факторы делятся на две группы: основные и вспомогательные (дополнительные). При этом число вспомогательных факторов -  , основных - (n-), число опытов - 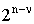. Если  =1, то план называется полурепликой от полного факторного эксперимента, если =2 √ 1/4 репликой, если =3 √ 1/8 репликой и так далее.

ПОЛУРЕПЛИКИ

Полуреплика √ это половина полного факторного эксперимента.

Рассмотрим пример при числе факторов n=3

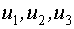
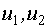-основные факторы.

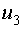- вспомогательный фактор.

Для построения матрицы дробного факторного эксперимента необходимо задать генерирующие соотношения (ГС), то есть определить, какому произведению основных факторов соответствует дополнительный фактор.

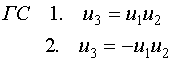
В дробном факторном эксперименте факторы всегда изменяются по плану полного факторного эксперимента типа 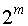, где m=n-.

u1	u2	u3
+1	+1	+1
-1	+1	-1
+1	-1	-1
-1	-1	+1

Матрица плана дробного факторного эксперимента обладает теми же свойствами, что и матрица полного факторного эксперимента. Матрица базисных функций, соответствующая дробному факторному эксперименту, так же удовлетворяет тем же свойствам, за исключением первого столбца, для которого не выполняется первое свойство.

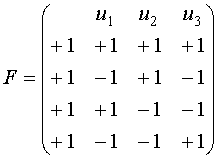
Вычисление оценок неизвестных коэффициентов модели производится по тем же формулам, что и для полного факторного эксперимента:

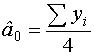
Таким образом, для дробного факторного эксперимента возникает явление смешивания оценок, то есть каждая алгебраическая сумма измерений выхода, деленная на число опытов, оценивает несколько истинных коэффициентов модели (в рассматриваемом случае два коэффициента - ).

Для определения так называемой разрешающей способности дробного факторного эксперимента строится таблица смешивания оценок:

Она определяет разрешающую способность ДФЭ.

Прежде чем разбить факторы на основные и дополнительные нужно иметь априорную информацию о наличии взаимодействия факторов. Имея таблицу смешивания, можно на основании априорной информации разбить факторы. Таблицу легко получить на основе определяющего контраста (ОК) √ выражения, получаемого на основе генерирующего соотношения. Определяющий контраст получается путем умножения левой и правой части генерирующего соотношения на левую часть.

Таблица смешивания коэффициентов получается следующим образом: каждая алгебраическая сумма является оценкой соответствующего коэффициента модели и коэффициента, который соответствует произведению факторов, получаемому при умножении правой части определяющего контраста на фактор, соответствующий алгебраической сумме.

В общем случае полуреплика пригодна лишь для построения линейных моделей без парных взаимодействий.

ЧЕТВЕРТЬРЕПЛИКИ

Рассмотрим пример при числе факторов n=5.

- основные факторы,

- вспомогательные факторы.

Для реплик высокой степени дробности вводится понятие обобщенного определяющего контраста (ООК), который получается из определяющих контрастов для всех дополнительных факторов.

Обобщенный определяющий контраст определяется путем приравнивания единице правых частей определяющих контрастов для всех дополнительных факторов и всевозможных их произведений.

Для 1/8 реплики в правой части ООК будет семь произведений факторов.

Наилучшей разрешающей способностью обладают те реплики, которые в качестве генерирующих соотношений используют произведения всех основных факторов. Анализ разрешающей способности реплик лучше проводить с помощью ЭВМ, используя пакет ⌠ПЛАНЭКС■.

Планы полного и дробного факторных экспериментов могут быть использованы для решения задач статической оптимизации объектов, подверженных действию случайных возмущений и помех.

Тема 13. Метод Бокса-Уилсона. Планирование второго порядка

Идея метода Бокса-Уилсона

Пример реализации метода Бокса-Уилсона

13.3. Назначение и типы планов второго порядка

13.4. Полный факторный эксперимент типа

13.5. Композиционные планы (ОЦКП, РЦКП)

ОЦКП