Расчет доверительных интервалов.

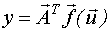
Задаем конкретное значение входа :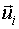

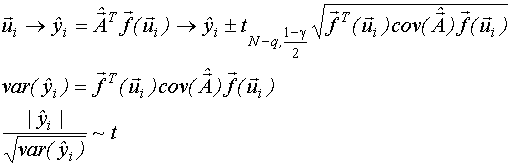
Доверительный интервал- это интервал возможных значений нашей величины.

В рассчитанный интервал с вероятностью 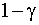попадает истинное значение .

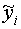Ширина доверительного интервала определяет точность модели регрессии. Чем уже доверительный интервал, тем более точная модель регрессии.

Тема 5. Построение моделей статики

В случае нелинейной параметризации

Нелинейные методы оценивания

Метод Гаусса-Ньютона

Метод Хартли

Метод Марквардта

Нелинейные методы оценивания

Нелинейно-параметризованная модель может быть представлена в виде: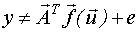

Оценивание неизвестных параметров нелинейно-параметризованных моделей возможно нелинейными методами наименьших квадратов. Наиболее распространенными являются:

метод Гаусса-Ньютона;
метод Хартли;
метод Марквардта.

Метод Гаусса-Ньютона

Имеется модель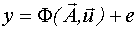
Задается исходное начальное приближение .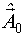
Функция регрессии раскладывается в ряд Тейлора в окрестности начального приближения, при этом в разложении используют только свободные член и линейный член, то есть осуществляют линеаризацию модели в окрестности .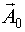

По МНК находят оценку 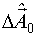, то есть оценку разности между истинным значением 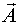и : .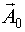
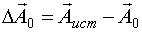Находится приближение: .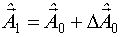
Далее функция раскладывается в ряд Тейлора в окрестности .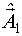
Находится 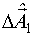и так далее.
Процедура заканчивается на той операции, на которой норма вектора 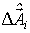становится меньше некоторой, достаточно малой, величины .

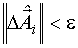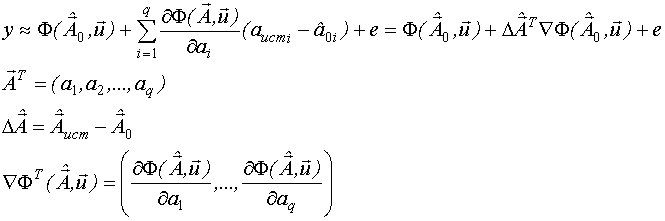
Получена линеаризованная по параметрам модель, в которой неизвестны коэффициенты 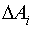. Оценка 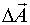возможна МНК.

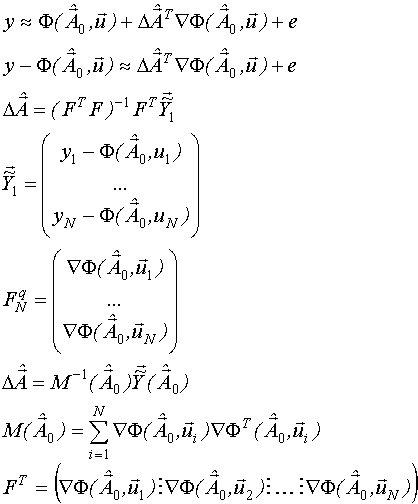
Каждый элемент суммы представляет собой матрицу размером q*q, являющуюся информационной матрицей Фишера для одного измерения входа-выхода.

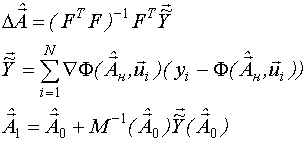
В общем виде алгоритм Гаусса-Ньютона можно записать следующим образом:

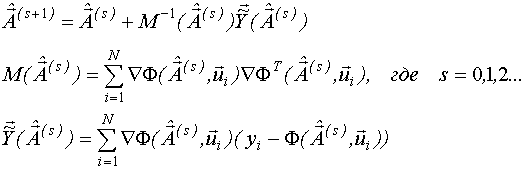
Метод Хартли

Процедура Хартли отличается от процедуры Гаусса-Ньютона тем, что используются не все значения 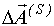, а только часть его.

Метод Марквардта

Метод Марквардта отличается тем, что вместо матрицы М используется матрица 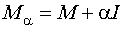, где I- единичная матрица. Говорят, что матрица 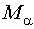лучше обусловлена (имеет определитель больше, чем у матрицы М).

Тема 6. Построение моделей динамики объектов управления

По экспериментальным данным

Понятие моделей динамики и их типы

Способы построения моделей импульсной переходной функции

Корреляционный метод идентификации

Методы решения уравнения Винера-Хопфа в дискретной форме

6.4.1. Вычисление оценки вектора неизвестных параметров на основе первых l уравнений

6.4.2. Вычисление оценки вектора неизвестных параметров на основе N>l уравнений

Использование корреляционного метода при подаче на вход псевдослучайного двоичного сигнала (ПСДС)