Нормальные линейные однородные системы дифференциальных уравнений с постоянными коэффициентами
Приведение системы с постоянными коэффициентами к одному дифференциальному уравнению дает линейное однородное или неоднородное дифференциальное уравнение с постоянными коэффициентами высшего порядка. Следовательно, структура решения такой системы дифференциальных уравнений должна быть аналогичной решению линейных дифференциальных уравнений.
Пусть дана нормальная система дифференциальных уравнений:
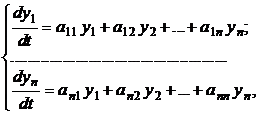
где 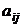 – постоянные коэффициенты. Как показано в п. 24, данную систему можно представить в матричном виде:
– постоянные коэффициенты. Как показано в п. 24, данную систему можно представить в матричном виде: 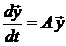 . Здесь
. Здесь 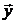 – матрица-столбец или вектор, составленный из решений системы,
– матрица-столбец или вектор, составленный из решений системы, 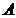 – матрица из коэффициентов системы.
– матрица из коэффициентов системы.
Будем искать решение системы в виде 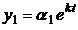 ,
, 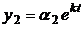 ,…,
,…, 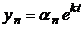 или
или 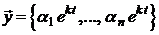 , поскольку лишь такое решение может удовлетворить всем уравнениям. Числа
, поскольку лишь такое решение может удовлетворить всем уравнениям. Числа 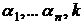 подлежат определению. Случай
подлежат определению. Случай 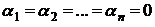 рассматривать не будем, так как он дает тривиальное решение системы.
рассматривать не будем, так как он дает тривиальное решение системы.
Для нахождения нетривиального решения подставим данные функции в систему:
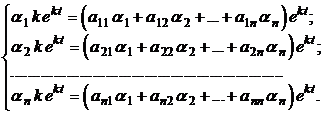
Сокращая все уравнения на 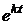 и перенося все члены в одну сторону, приходим к однородной системе линейных алгебраических уравнений:
и перенося все члены в одну сторону, приходим к однородной системе линейных алгебраических уравнений:
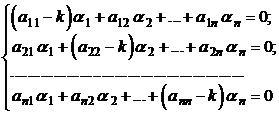 (3.22.1)
(3.22.1)
или в матричной форме 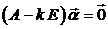 , где
, где 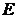 – единичная матрица
– единичная матрица 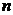 -го порядка,
-го порядка, 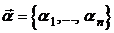 .
.
Чтобы однородная система линейных алгебраических уравнений имела не тривиальное решение, необходимо чтобы ее определитель был равен нулю. В результате мы приходим к уравнению 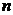 -го порядка для определения
-го порядка для определения 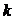 :
:
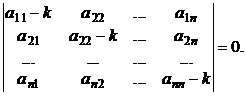
Это уравнение называется характеристическим уравнением системы, а его корни – корнями характеристического уравнения.
Рассмотрим несколько случаев корней характеристического уравнения.
1. Корни характеристического уравнения действительные и различные. Обозначим через 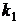 ,
, 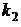 ,…,
,…, 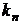 корни характеристического уравнения. Для каждого корня решим систему (3.22.1), определяя коэффициенты
корни характеристического уравнения. Для каждого корня решим систему (3.22.1), определяя коэффициенты 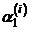 ,
, 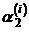 ,…,
,…, 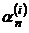 . Система (3.22.1) имеет ранг матрицы на единицу меньше ее порядка, то есть одна переменная является свободной. Обычно ее полагают равной единице.
. Система (3.22.1) имеет ранг матрицы на единицу меньше ее порядка, то есть одна переменная является свободной. Обычно ее полагают равной единице.
Таким образом, получаем
для 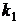 –
– 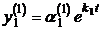 ,
, 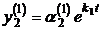 ,…,
,…, 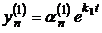 ;
;
для 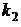 –
– 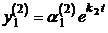 ,
, 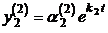 ,…,
,…, 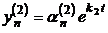 ;
;
для 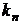 –
– 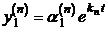 ,
, 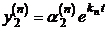 ,…,
,…, 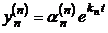 .
.
Решением системы будет линейная комбинация полученных функций:
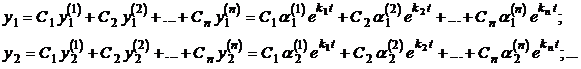
Определитель Вронского, составленный для функций 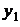 ,
, 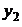 ,…,
,…, 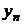 , в ноль не обращается, следовательно, это действительно будет общее решение системы линейных однородных дифференциальных уравнений в данном случае.
, в ноль не обращается, следовательно, это действительно будет общее решение системы линейных однородных дифференциальных уравнений в данном случае.
2. Корни характеристического уравнения действительные и кратные. В том случае, когда какой-то корень характеристического уравнения системы, например первый, является действительным и имеет кратность 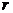 , то по аналогии с линейными дифференциальными уравнениями
, то по аналогии с линейными дифференциальными уравнениями 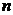 -го порядка общее решение приобретет вид:
-го порядка общее решение приобретет вид:
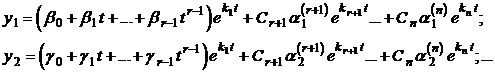
Чтобы определить неизвестные коэффициенты 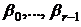 ,
, 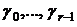 ,… подставляют функции
,… подставляют функции 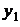 ,
, 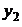 ,…,
,…, 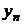 в систему дифференциальных уравнений и приравнивают коэффициенты при одинаковых степенях
в систему дифференциальных уравнений и приравнивают коэффициенты при одинаковых степенях 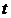 .
.
3. Корни характеристического уравнения различные, но среди них есть комплексные. Пусть среди корней характеристического уравнения есть два комплексных: 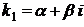 ,
, 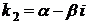 . Этим корням будут соответствовать решения:
. Этим корням будут соответствовать решения:
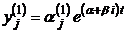 ,
, 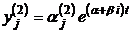 ,
,
где 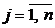 . Коэффициенты
. Коэффициенты 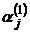 и
и 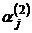 определяются из системы (3.22.1). Затем, составляя линейную комбинацию из этих решений по аналогии с линейными дифференциальными уравнениями
определяются из системы (3.22.1). Затем, составляя линейную комбинацию из этих решений по аналогии с линейными дифференциальными уравнениями 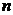 -го порядка, получаем два частных решения:
-го порядка, получаем два частных решения: