Понятие определителя. Решение систем линейных уравнений методами Крамера (определителей), Гаусса, обратных матриц

В этом разделе речь пойдет о различных способах решения систем линейных уравнений. Рассмотрим сначала некоторые определения

Определения 5.2(1)

Решением системы линейных уравнений с n неизвестными называется такой набор чисел (с₁ ,с₂ ,…, с_n), что при его подстановке в систему вместо соответствующих неизвестных (с₁ вместо х₁, ..., с_n вместо х_n) каждое из уравнений системы обращается в тождество.

Если система имеет хотя бы одно решение, она называется совместной, система, не имеющая ни одного решения, называется несовместной.

Система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы линейных уравнений с одинаковым числом неизвестных называются эквивалентными, если множества всех решений этих систем совпадают.

Если свободные члены b₁ = b₂ = …=b_m = 0, то система называется однородной, в противном случае она называется неоднородной. Однородная система (независимо от числа уравнений) всегда имеет решение, состоящее из нулевых значений для всех неизвестных.

Пусть имеется матрица A = (a_ij) коэффициентов системы размерности m ´ n, n-мерный вектор-столбец X и m-мерный вектор-столбец B. Матрица с добавленным столбцом свободных членов называется расширенной матрицей системы.

(вертикальная черта проводится для удобства и просто зрительно отделяет добавленный столбец)

Рассмотрим систему двух линейных уравнений с двумя неизвестными в общем виде (в школьной программе подобные системы рассматриваются с неизвестными x и y, а не x₁ и x₂ , но это вопрос обозначений, кроме того, при обозначении неизвестных одной буквой с разными индексами сразу видно, сколько в системе неизвестных))

.

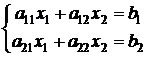Найдем x₁ следующим образом: чтобы исключить x₂, умножим первое уравнение на a₂₂ и из полученного уравнения вычтем второе, умноженное на a₁₂:

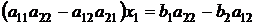. (1)

Обозначим D = a₁₁a₂₂ – a₁₂a₂₁, D₁ = b₁a₂₂ – b₂a₁₂.

Для определения x₂ поступим так: умножим второе уравнение на a₁₁ и из полученного уравнения вычтем первое, умноженное на a₂₁:

(a₁₁a₂₂ – a₁₂a₂₁)x_{2 =} a₁₁b₂ – a₂₁b₁. (2)

Обозначим D₂ = a₁₁b₂ – a₂₁b₁.

Из (1) и (2) видно, что если D ¹ 0, то система имеет решение, определяемое формулой

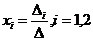. (3)

Замечание 5.2(1)

Из (1) и (2) следует, что если решение существует, то оно единственным образом выражается через коэффициенты системы и свободные члены. Чтобы доказать существование, надо подставить две формулы (3) в систему и убедиться в том, что оба уравнения обращаются в верные равенства

Определения 5.2(1)

Величина D называется определителем матрицы второго порядка

.

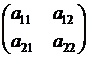Определителем произвольной матрицы второго порядка 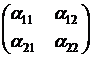называется число, которое обозначается 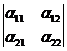и равно произведению двух чисел, стоящих на главной диагонали минус произведение двух чисел, стоящих на другой диагонали:

a₁₁a₂₂ – a₁₂a₂₁.

Например,

.

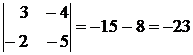Из сказанного следует, что величины D₁ и D₂ в (3) тоже являются определителями:

.

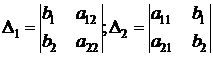Рассмотрим теперь систему трех линейных уравнений с тремя неизвестными:

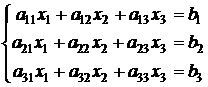. (4)

Определение 5.2(2)

Определителем произвольной квадратной матрицы третьего порядка 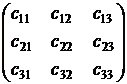называется сумма шести слагаемых, каждое из которых представляет собой произведение трех элементов матрицы, выбираемых по следующему правилу: три произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников: 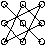, берутся со знаком "+", а три произведения элементов, стоящих на второй диагонали и в вершинах двух других треугольников: 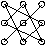, берутся со знаком "-". Определитель третьего порядка обозначается так:

.

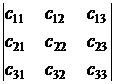Например,

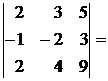
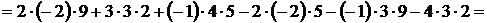
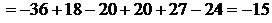
Решая систему (4), например методом Гаусса (см ниже), можно получить равенства

D×x₁ = D₁; D×x₂ = D₂; D×x₃ = D₃, (5)

где

.

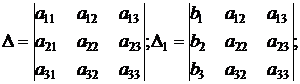
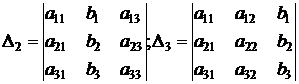Из формул (5) видно, что если D ¹ 0, то единственным образом определяется решение системы:

.

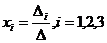Решая квадратные системы линейных уравнений 4-го, 5-го или любого более высокого порядка, можно получить формулы, аналогичные формулам (1), (2) или (5).

Данный метод решения системы линейных уравнений называется методом определителей (методом Крамера(см ниже),

Определение 5.2(1).

Система линейных уравнений называется однородной, если все ее свободные члены равны нулю. Однородная система (независимо от числа уравнений) всегда имеет решение, состоящее из нулевых значений для всех неизвестных.

Определение 5.2(2).

Определителем квадратной матрицы n-го порядка или просто определителем n-го порядка называется сумма n! слагаемых. Каждое слагаемое представляет собой произведение n элементов, взятых по одному из каждой строки и каждого столбца определителя . (Произведения отличаются одно от другого набором элементов.) Перед каждым произведением ставится знак "+" или "-"по определенному правилу.

Если при записи матрица заключается в большие круглые скобки, то ее определитель записывается в больших «прямых» скобках (слева и справа ставятся вертикальные линии).

Замечание 5.2(1) :

Помимо термина "определитель" часто используется термин "детерминант" и определитель матрицы A обозначается detA.

Разберем теперь правило знаков для определителя:

Так как в каждом произведении присутствует один элемент из 1-й строки, один элемент из 2-ой и т.д., то произведение в общем виде можно записать так:

a_1i×a_2j×a_3k×¼×a_ns.

Здесь i, j, k, ¼, s – номера столбцов, в которых стоят элементы, выбранные из 1-й, 2-й, 3-й, ... n-й строк, соответственно. Ясно из сказанного выше, что каждое из чисел i, j, k, ¼, s равно какому-либо из чисел 1, 2, ..., n, и что все числа i, j, k, ¼, s – различные.

Расположенные в данном порядке

i, j, k, ¼, s,

эти числа образуют "перестановку" из чисел 1, 2, ..., n (перестановкой называется заданный порядок в конечном множестве. Более подробно см Лекцию 6).

Определения 5.2(3)

Взаимное расположение двух чисел в перестановке, когда большее стоит впереди меньшего называется инверсией. Например, в перестановке 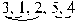три инверсии; в перестановке 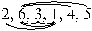– шесть инверсий.

Перестановка называется четной, если в ней четное число инверсий и нечетной, если число инверсий нечетное.

Теперь сформулируем правило:

произведение a_1i×a_2j×a_3k×¼×a_ns берется со знаком "+", если вторые индексы образуют четную перестановку, и со знаком "-", если нечетную.

Из определения определителя можно вывести следующие его свойства:

Свойства определителей:

1. Если поменять местами две строки определителя (два столбца), то получим новый определитель, равный исходному, умноженному на .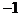

2. Определитель, имеющий две равных строки (два равных столбца), равен нулю. Определитель матрицы с пропорциональными строками (одна строка есть другая, умноженная на некоторое ненулевое число)

3. Если одну из строк определителя умножить на какое-либо число, то получится определитель, равный исходному, умноженному на это число (и обратно, строку (столбец) можно разделить на одно и то же число, и вынести множитель за знак определителя).

4. Определитель произведения матриц есть произведение определителей исходных матриц

5. Определитель транспонированной матрицы равен определителю исходной матрицы.

6. Определитель треугольной матрицы (матрица, у которой по главной диагонали и над(под) ней стоят некие элементы, а все остальные – нули) равен произведению элементов главной диагонали

7. Определитель ступенчатой матрицы равен произведению определителей диагональных клеток

8. Если в определителе вместо любой строки записать сумму этой строки и любой другой строки, умноженной на некоторое число, то полученный новый определитель будет равен исходному.

9.Разложение определителя по строке (столбцу)

До сих пор было показано, как вычислять определитель второго и третьего порядков. Чтобы вычислить определитель более высоких порядков, пользуются формулой Лапласа разложения определителя по строке или столбцу:

detA = a_i1(–1)ⁱ⁺¹M _i1 + a_i2(–1)ⁱ⁺²M _i2 +¼+ a_in(–1)ⁱ⁺ⁿM _in =

₌ a_1j (–1) ^1+jM _1j + a_2j(–1)^2+jM _2j +¼+ a_nj(–1) ^n+jM _nj

Здесь i и j — любые числа от 1 до n. Последняя формула представляет собой разложение определителя по i-й строке или j-му столбцу. Поясним последнюю формулу:

Определения 5.2(4).

M_ij называется минором и равняется определителю порядка n – 1, который получается из определителя исходной матрицы detA, если вычеркнуть i-ю строку и j-й столбец. Произведение
(–1)^i+jM_ij обозначается A_ij и называется алгебраическим дополнением элемента a_ij.

Пусть D – определитель четвертого порядка: 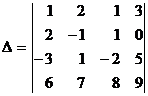. Представим его разложение по второй строке:

,

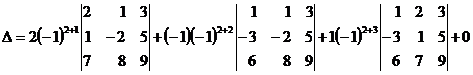и по второму столбцу:

.

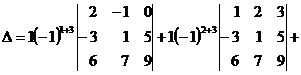
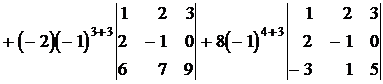Аналогичным образом можно вычислить D, разлагая его по первой, третьей, четвертой строке или по первому, второму или четвертому столбцу.

Вычисление определителя четвертого порядка сводится в худшем случае (если среди элементов нет нулей) к вычислению четырех определителей третьего порядка.

Аналогичным образом вычисление определителя 5-го порядка сводится к вычислению 5-ти определителей 4-го порядка и т.д.

Комбинируя различные действия над матрицами и свойства определителей можно существенно упростить задачу нахождения значений большого количества громоздких слагаемых-множителей определителя.