Матрицы. Действия над матрицами

Лекция 5. Матрицы

5.1..Матрицы. Действия над матрицами.

5.2. Понятие определителя. Решение систем линейных уравнений методами Крамера (определителей), Гаусса, обратных матриц

Программные положения

Теорию матриц можно рассматривать и как раздел дискретной математики и как раздел алгебры. Матрицы широко используются и при обработке результатов психологических экспериментов (в первую очередь это матрица первичных данных и корреляционная матрица)

Методические рекомендации

Прочитайте текст лекции, выполните упражнения. Рассмотрите различные способы решения системы линейных уравнений. Обратите внимание на условия совместности системы линейных уравнений.

Литература

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Часть I «Линейная алгебра» Глава 1 «Линейные уравнения. Идеи и примеры» (стр.12-30), глава 2 «Линейные уравнения» (стр.30-51), глава 3»Векторы и матрицы» (стр 51-61)

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XVIII «Определители второго и третьего порядка» (стр. 307-324)

Дополнительно

Д.К.Фаддеев «Лекции по алгебре» Глава V «Матрицы и определители» (стр. 72-142)

Контрольные вопросы:

1. Что такое матрица? Что определяют два нижних индекса ее элементов?

2. Какие бывают матрицы? Приведите примеры

3. Какие действия можно выполнять над матрицами?

4. Что такое определитель квадратной матрицы?

5. Доказать, что слагаемых-произведений, входящих в формулу определителя, отличающихся одно от другого набором элементов существует ровно n!

6. Докажите, что определитель треугольной матрицы равен произведению элементов главной диагонали

7. Если матрицы А и В можно умножать, следует ли из этого, что их можно складывать? Если матрицы А и В можно складывать, следует ли из этого, что их можно умножать?

Можно ли умножить квадратную матрицу на неквадратную? Может ли произведение неквадратных матриц быть квадратной матрицей?

8. Может ли при умножении ненулевых матриц получиться нулевая матрица?

9. Могут ли совпадать матрицы А и АТ?

10. Опишите 3 способа решения систем линейных уравнений (метод определителей (Крамера), метод Гаусса и метод обратных матриц)

11. Решите тремя способами систему

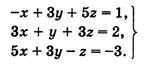
12. Решите уравнение

9. Сформулируйте и докажите свойства обратных матриц

Определения 5.1(1)

Матрицей А размера m 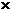n называется прямоугольная таблица из m строк и n столбцов, состоящая из чисел или иных математических выражений a_ij –(называемых элементами матрицы), i = 1,2,...,m, j = 1,2,. ..,n. Матрицы обозначаются заглавными латинскими буквами, сама таблица берется в круглые скобки.

С другой стороны , для положительных целых чисел m и n матрицей m 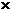n, или массивом m 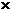n, называется функция

A: {1,2,…,m} 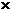{1,2,…,n}→ D

где D — это, как правило, множество действительных, комплексных, рациональных или целых чисел.

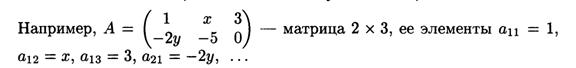
Главная диагональ матрицы– диагональ из левого верхнего в правый нижний угол ее элементы имеют вид a_ii

Квадратной матрицей n-го порядка называется матрица размера n х n.

Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали (т. е. с индексами i≠ j) равны нулю.

Единичной (обозначается Е) называется диагональная матрица с единицами на главной диагонали.

Нулевой называется матрица, все элементы которой равны нулю.

Треугольная матрица – матрица, у которой по главной диагонали и выше(ниже) нее идут ненулевые элементы, а все остальные равны нулю.

Ступенчатой называется матрица, состоящая из квадратных матриц, часть из которых – по главной диагонали и выше(ниже) ненулевые, а остальные – нулевые.

(«образующих ступеньку»)

Определение 5.1(2)

Две матрицы одинаковой размерности m ´ n называются равными, если в них одинаковые места заняты одними и теми же элементами (на пересечении i-й строки и j-го столбца в одной и в другой матрице стоит тот же элеменгт; i=1, 2, ..., m; j=1, 2, ..., n).

Примеры 5.1.

1)квадратная матрица 3х3

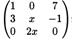
2)диагональная матрица

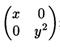
3)единичная

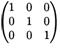
4)нулевая

5)ступенчатая

(А О)

В С , где А, В и С – квадратные матрицы, О – квадрат из нулей

Еще один вариант определения матрицы – это таблица коэффициентов системы (линейных) уравнений

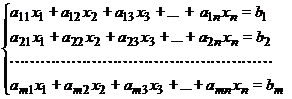
И система эта в матричной записи выглядит следующим образом:

AX = B, где А – матрица коэффициентов, Х – столбец неизвестных, а В – столбец свободных членов (об умножении матриц см.далее):

;

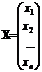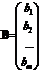
Замечание 5.1.

Для произвольной матрицы элементы а_ij могут иметь произвольную, необязательно числовую природу.

Действия над матрицами

1. Умножение на число

Пусть A = (a_ij) – некоторая матрица и a – произвольное число, тогда aA = (aa_ij), то есть при умножении матрицы A на число a все числа, составляющие матрицу A, умножаются на число a. (Соответственно, можно выносить общий множитель всех элементов множителем за знак матрицы)

2. Сложение матриц

Пусть A и B – матрицы одинаковой размерности A = (a_ij), B = (b_ij), тогда их сумма A + B – матрица C = (c_ij) той же размерности, опреде­ляемая из формулы c_ij = a_ij + b_ij, то есть при сложении двух матриц попарно складываются одинаково расположенные в них числа.

Найдем в качестве примера матрицу С=2А+3В, где

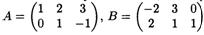
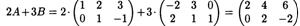
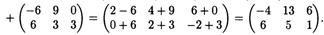
3. Умножение матриц

Матрицу A можно умножить на матрицу B, то есть найти матрицу C = AB, если число столбцов n матрицы A равно числу строк матрицы B, при этом матрица C будет иметь столько строк, сколько строк у матрицы A и столько столбцов, сколько столбцов у матрицы B. Каждый элемент матрицы C определяется формулой

.

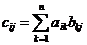Элемент c_ij матрицы-произведения C равен сумме произведений элементов i-й строки первой матрицы- сомножителя на соответствующие элементы j-го столбца второй матрицы-сомножителя.

Из сказанного следует, что если можно найти произведение матриц AB, то произведение BA, вообще говоря, тем самым не определено.

Приведем примеры перемножения матриц:

1) =

= =

= ;

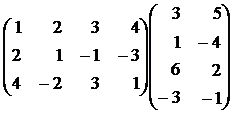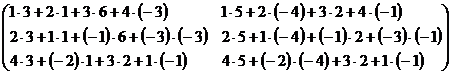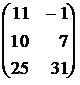2) 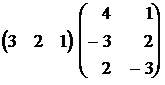= (8, 4).

Если AB и BA одновременно определены, то, вообще говоря, эти произведения не равны. Это означает, что умножение матриц не коммутативно. Продемонстрируем это на примере.

.

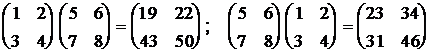Для сложения и умножения матриц справедливы следующие законы:

1) A + B = B+ A;

2) a (A + B) = aA + aB; a - число

3) (A +B) + C = A + (B + C);

4)(AB)C = A(BC);

5)A(B + C) =AB + AC.

Замечание

Рассмотрим квадрат матрицы А², описывающей граф, из начала лекции

=

Полученная матрица снова имеет отношение к рассматриваемому графу. Она показывает теперь количество путей длины 2 (включающих 2 ребра, ). а₂₂ =3, например, означает пути 2-1 и 1-2, 2-3 и 3-2, 2-4 и 4-2, всего 3.

В общем случае Аⁿ описывает число путей длины n.

4. Транспонирование

Транспонированной к матрице А = (а_ij) называется матрица

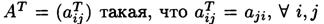
(А^Т – это не степень, а обозначение транспонирования)

Т.е. все строки исходной матрицы становятся столбцами транспонированной

Свойства операции транспонирования

1. (А^Т )^Т = А^Т

2. (А + В)^Т = А^Т + В^Т

3. (АВ)^Т = В^Т А^Т

Доказательство:

Пусть

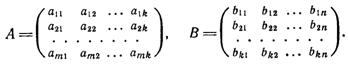
Положим

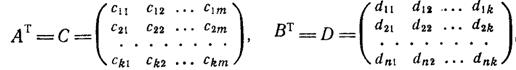
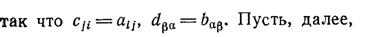
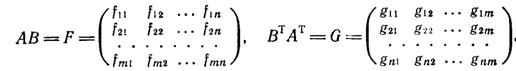
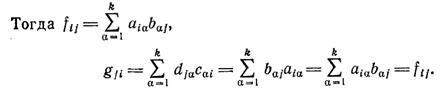
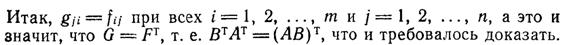
Итак, над матрицами определены 4 действия: сложение, умножение на число, умножение матрицы на матрицу и транспонирование

Условие применимости и размеры результата приведены на нижеследующих схемах:

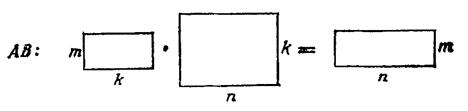
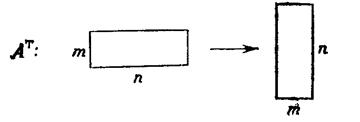
Эти действия обладают свойствами:

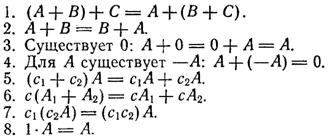
Это – свойства векторного пространства, так что матрицы фиксированных размеров образуют векторное пространство

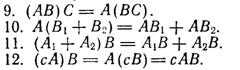
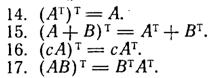
Для квадратных матриц фиксированного порядка n действия сложения и умножения определены всегда , и их результатами являются квадратные матрицы того же порядка. Таким образом, квадратные матрицы фиксированного порядка образуют кольцо. Кольцо, наделенное структурой векторного пространства, т.е. система объектов, обладающих свойствами 1-12 называется алгеброй над основным полем. Таким образом, квадратные матрицы с элементами из поля К составляют алгебру над этим полем.

Более подробно об этих и других алгебраических структурах см. А.В.Дорофеева «Высшая математика» Глава 3 «Алгебраические структуры» стр. 53-71 и

Д.К.Фаддеев «Лекции по алгебре» Глава 1 § 3 «Некоторые общие вопросы алгебры» стр.21-25

Определения 5.1(3)

Матрицы фиксированной структуры с элементами из некоторого поля К образуют векторное пространство S. (Элементы поля К называют числами, хотя они могут иметь иную природу) Векторное пространство – абелева группа (набор элементов с определенными на них бинарной ассоциативной коммутативной операцией, единицей и обратным элементом), для элементов которой определены действия.

с(А+В) = сА+сВ

(с+d)A = cA+dA

c(dA)=(cd)A

1· A = A

А, В – матрицы, с,d – элементы поля К

Определения 5.1(4)

Матрица, состоящая из одной строки, называется вектором (вектором-строкой). Матрица, состоящая из одного столбца, также называется вектором (вектором-столбцом).

Определения 5.1(5)

Элементарными преобразованиями матрицы называются следующие операции:

1. Перемена местами двух строк (столбцов).

2. Умножение строки (столбца) на число, отличное от нуля.

3. Прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца). Замена строки матрицы суммой этой строки с любой другой строкой, умноженной на некоторое число

(Сравните: действия над уравнениями системы линейных уравнений при ее решении)

Матрица В, полученная из матрицы А с помощью элементарных преобразований, называется эквивалентной матрице А (обозначается В~А).

Определения 5.2(1)

Решением системы линейных уравнений с n неизвестными называется такой набор чисел (с₁ ,с₂ ,…, с_n), что при его подстановке в систему вместо соответствующих неизвестных (с₁ вместо х₁, ..., с_n вместо х_n) каждое из уравнений системы обращается в тождество.

Если система имеет хотя бы одно решение, она называется совместной, система, не имеющая ни одного решения, называется несовместной.

Система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы линейных уравнений с одинаковым числом неизвестных называются эквивалентными, если множества всех решений этих систем совпадают.

Если свободные члены b₁ = b₂ = …=b_m = 0, то система называется однородной, в противном случае она называется неоднородной. Однородная система (независимо от числа уравнений) всегда имеет решение, состоящее из нулевых значений для всех неизвестных.

Пусть имеется матрица A = (a_ij) коэффициентов системы размерности m ´ n, n-мерный вектор-столбец X и m-мерный вектор-столбец B. Матрица с добавленным столбцом свободных членов называется расширенной матрицей системы.

(вертикальная черта проводится для удобства и просто зрительно отделяет добавленный столбец)

Рассмотрим систему двух линейных уравнений с двумя неизвестными в общем виде (в школьной программе подобные системы рассматриваются с неизвестными x и y, а не x₁ и x₂ , но это вопрос обозначений, кроме того, при обозначении неизвестных одной буквой с разными индексами сразу видно, сколько в системе неизвестных))

.

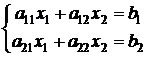Найдем x₁ следующим образом: чтобы исключить x₂, умножим первое уравнение на a₂₂ и из полученного уравнения вычтем второе, умноженное на a₁₂:

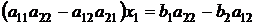. (1)

Обозначим D = a₁₁a₂₂ – a₁₂a₂₁, D₁ = b₁a₂₂ – b₂a₁₂.

Для определения x₂ поступим так: умножим второе уравнение на a₁₁ и из полученного уравнения вычтем первое, умноженное на a₂₁:

(a₁₁a₂₂ – a₁₂a₂₁)x_{2 =} a₁₁b₂ – a₂₁b₁. (2)

Обозначим D₂ = a₁₁b₂ – a₂₁b₁.

Из (1) и (2) видно, что если D ¹ 0, то система имеет решение, определяемое формулой

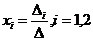. (3)

Замечание 5.2(1)

Из (1) и (2) следует, что если решение существует, то оно единственным образом выражается через коэффициенты системы и свободные члены. Чтобы доказать существование, надо подставить две формулы (3) в систему и убедиться в том, что оба уравнения обращаются в верные равенства

Определения 5.2(1)

Величина D называется определителем матрицы второго порядка

.

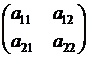Определителем произвольной матрицы второго порядка 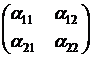называется число, которое обозначается 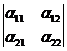и равно произведению двух чисел, стоящих на главной диагонали минус произведение двух чисел, стоящих на другой диагонали:

a₁₁a₂₂ – a₁₂a₂₁.

Например,

.

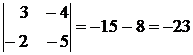Из сказанного следует, что величины D₁ и D₂ в (3) тоже являются определителями:

.

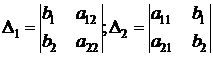Рассмотрим теперь систему трех линейных уравнений с тремя неизвестными:

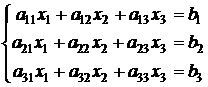. (4)

Определение 5.2(2)

Определителем произвольной квадратной матрицы третьего порядка 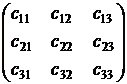называется сумма шести слагаемых, каждое из которых представляет собой произведение трех элементов матрицы, выбираемых по следующему правилу: три произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников: 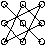, берутся со знаком "+", а три произведения элементов, стоящих на второй диагонали и в вершинах двух других треугольников: 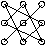, берутся со знаком "-". Определитель третьего порядка обозначается так:

.

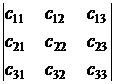Например,

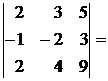
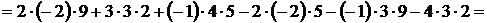
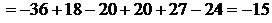
Решая систему (4), например методом Гаусса (см ниже), можно получить равенства

D×x₁ = D₁; D×x₂ = D₂; D×x₃ = D₃, (5)

где

.

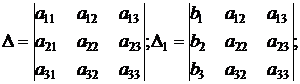
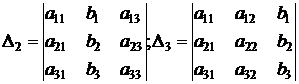Из формул (5) видно, что если D ¹ 0, то единственным образом определяется решение системы:

.

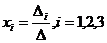Решая квадратные системы линейных уравнений 4-го, 5-го или любого более высокого порядка, можно получить формулы, аналогичные формулам (1), (2) или (5).

Данный метод решения системы линейных уравнений называется методом определителей (методом Крамера(см ниже),

Определение 5.2(1).

Система линейных уравнений называется однородной, если все ее свободные члены равны нулю. Однородная система (независимо от числа уравнений) всегда имеет решение, состоящее из нулевых значений для всех неизвестных.

Определение 5.2(2).

Определителем квадратной матрицы n-го порядка или просто определителем n-го порядка называется сумма n! слагаемых. Каждое слагаемое представляет собой произведение n элементов, взятых по одному из каждой строки и каждого столбца определителя . (Произведения отличаются одно от другого набором элементов.) Перед каждым произведением ставится знак "+" или "-"по определенному правилу.

Если при записи матрица заключается в большие круглые скобки, то ее определитель записывается в больших «прямых» скобках (слева и справа ставятся вертикальные линии).

Замечание 5.2(1) :

Помимо термина "определитель" часто используется термин "детерминант" и определитель матрицы A обозначается detA.

Разберем теперь правило знаков для определителя:

Так как в каждом произведении присутствует один элемент из 1-й строки, один элемент из 2-ой и т.д., то произведение в общем виде можно записать так:

a_1i×a_2j×a_3k×¼×a_ns.

Здесь i, j, k, ¼, s – номера столбцов, в которых стоят элементы, выбранные из 1-й, 2-й, 3-й, ... n-й строк, соответственно. Ясно из сказанного выше, что каждое из чисел i, j, k, ¼, s равно какому-либо из чисел 1, 2, ..., n, и что все числа i, j, k, ¼, s – различные.

Расположенные в данном порядке

i, j, k, ¼, s,

эти числа образуют "перестановку" из чисел 1, 2, ..., n (перестановкой называется заданный порядок в конечном множестве. Более подробно см Лекцию 6).

Определения 5.2(3)

Взаимное расположение двух чисел в перестановке, когда большее стоит впереди меньшего называется инверсией. Например, в перестановке 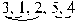три инверсии; в перестановке 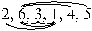– шесть инверсий.

Перестановка называется четной, если в ней четное число инверсий и нечетной, если число инверсий нечетное.

Теперь сформулируем правило:

произведение a_1i×a_2j×a_3k×¼×a_ns берется со знаком "+", если вторые индексы образуют четную перестановку, и со знаком "-", если нечетную.

Из определения определителя можно вывести следующие его свойства:

Свойства определителей:

1. Если поменять местами две строки определителя (два столбца), то получим новый определитель, равный исходному, умноженному на .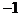

2. Определитель, имеющий две равных строки (два равных столбца), равен нулю. Определитель матрицы с пропорциональными строками (одна строка есть другая, умноженная на некоторое ненулевое число)

3. Если одну из строк определителя умножить на какое-либо число, то получится определитель, равный исходному, умноженному на это число (и обратно, строку (столбец) можно разделить на одно и то же число, и вынести множитель за знак определителя).

4. Определитель произведения матриц есть произведение определителей исходных матриц

5. Определитель транспонированной матрицы равен определителю исходной матрицы.

6. Определитель треугольной матрицы (матрица, у которой по главной диагонали и над(под) ней стоят некие элементы, а все остальные – нули) равен произведению элементов главной диагонали

7. Определитель ступенчатой матрицы равен произведению определителей диагональных клеток

8. Если в определителе вместо любой строки записать сумму этой строки и любой другой строки, умноженной на некоторое число, то полученный новый определитель будет равен исходному.

9.Разложение определителя по строке (столбцу)

До сих пор было показано, как вычислять определитель второго и третьего порядков. Чтобы вычислить определитель более высоких порядков, пользуются формулой Лапласа разложения определителя по строке или столбцу:

detA = a_i1(–1)ⁱ⁺¹M _i1 + a_i2(–1)ⁱ⁺²M _i2 +¼+ a_in(–1)ⁱ⁺ⁿM _in =

₌ a_1j (–1) ^1+jM _1j + a_2j(–1)^2+jM _2j +¼+ a_nj(–1) ^n+jM _nj

Здесь i и j — любые числа от 1 до n. Последняя формула представляет собой разложение определителя по i-й строке или j-му столбцу. Поясним последнюю формулу:

Определения 5.2(4).

M_ij называется минором и равняется определителю порядка n – 1, который получается из определителя исходной матрицы detA, если вычеркнуть i-ю строку и j-й столбец. Произведение
(–1)^i+jM_ij обозначается A_ij и называется алгебраическим дополнением элемента a_ij.

Пусть D – определитель четвертого порядка: 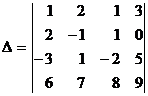. Представим его разложение по второй строке:

,

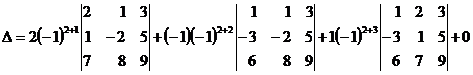и по второму столбцу:

.

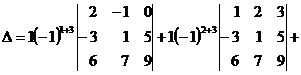
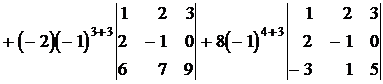Аналогичным образом можно вычислить D, разлагая его по первой, третьей, четвертой строке или по первому, второму или четвертому столбцу.

Вычисление определителя четвертого порядка сводится в худшем случае (если среди элементов нет нулей) к вычислению четырех определителей третьего порядка.

Аналогичным образом вычисление определителя 5-го порядка сводится к вычислению 5-ти определителей 4-го порядка и т.д.

Комбинируя различные действия над матрицами и свойства определителей можно существенно упростить задачу нахождения значений большого количества громоздких слагаемых-множителей определителя.

Определение 5.2(5).

Система линейных уравнений называется однородной, если все ее свободные члены равны нулю. Однородная система (независимо от числа уравнений) всегда имеет решение, состоящее из нулевых значений для всех неизвестных. Для однородных систем представляет интерес вопрос о том, является ли нулевое решение единственным или кроме него существуют другие, нетривиальные решения

Следствие 3. Для того, чтобы система n линейных однородных уравнений с n неизвестными имела нетривиальные решения, необходимо, чтобы определитель матрицы из ее коэффициентов был равен нулю.

Действительно, если хотя бы одно нетривиальное решение имеется, то система имеет более чем одно решение, так как нулевое всегда есть. Следовательно, определитель матрицы из коэффициентов системы равен нулю.

Метод обратных матриц

Рассмотрим уравнение в матричной форме АХ = В, Где А – матрица коэффициентов системы, Х – столбец неизвестных, В – столбец свободных членов.

Если бы речь шла об «обычном числовом» уравнении ax = b, a≠0, оно решалось бы умножением обеих частей уравнения на обратный к а элемент а^-1 (1/a (делением на а))

1/a· ax = 1/a ·b и тогда x = b/a.

Тогда для уравнения АХ=В,

А^-1 АХ = А^-1 В, откуда решение находится по формуле Х = А^-1 В, где А^-1 - матрица, обратная к исходной матрице А

Это рассуждение применимо и к матричным уравнениям AX=B, где В является некоторой матрицей, необязательно вектор-столбцом. Х в таком случае будет просто некоторой матрице (см пример 5.2).

Определение 5.2(6).

Пусть A = (a_ij) – квадратная матрица с определителем, не равным нулю.

Тогда существует обратная матрица A^–1, такая, что АA^–1 = A^–1А = Е (единичной матрице).

Найти обратную к А матрицу можно по формуле

.

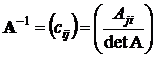Последняя формула означает, что в i-й строке и j-м столбце обратной матрицы располагается алгебраическое дополнение элемента, стоящего в j-й строке и в i-м столбце исходной матрицы, деленное на определитель исходной матрицы.

Иначе говоря, обратная матрица находится делением на определитель исходной матрицы так называемой союзной матрицы – матрица, транспонированной к матриений (см. опр. 5.2(4)

.

Пример 5.2(1):

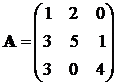detA = 20 + 6 – 24 = 2;

.

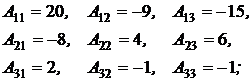
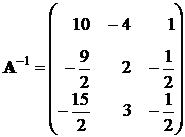Из определения обратной матрицы следует, что она существует только для квадратной матрицы с определителем, отличным от нуля.

Свойства обратной матрицы

1. det A^-1 = (det A)^-1

Действительно, А A^-1 = Е, следовательно, detA det A^-1 = detE=1, откуда (det A)^-1 =

=det A^-1

2. Если А и В невырожденны, то их произведение АВ тоже невырожденно и

(АВ)^-1 = В^-1 А^-1, то есть, матрица, обратная к произведению, равна произведению обратных, взятых в обратном порядке.

Действительно, (В^-1 А^-1)(АВ) = В^-1 (А^-1 А)В = В^-1 В = Е.

Отсюда следует, что В^-1 А^-1 = (АВ)^-1

3.(А^-1 )^-1 = А

Действительно, (А^-1 )^-1 есть такая единственная матрица, произведение которой на А^-1 равно Е. Этим свойством обладает А

4. (А^Т )^-1 = (А^-1 )^Т .

Действительно, переходя в равенстве А А^-1 = Е к транспонированным матрицам, получим (А^Т )^-1 А^Т = Е, откуда следует, что (А^Т )^-1 = (А^Т )^-1

Пример 5.2(2)

Решить матричное уравнение АХ=В

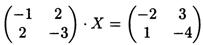
Будем искать решение в виде Х=А^-1 В , т.к. А^-1АХ = А^-1 В

Найдем определитель матрицы А

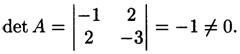
Определитель не равен нулю, значит, существуют единственное решение уравнения и матрица, обратная к матрице А. Найдем ее:

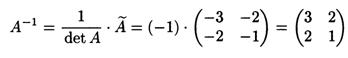
Теперь найдем решение уравнения

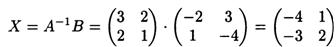
Лекция 5. Матрицы

5.1..Матрицы. Действия над матрицами.

5.2. Понятие определителя. Решение систем линейных уравнений методами Крамера (определителей), Гаусса, обратных матриц

Программные положения

Теорию матриц можно рассматривать и как раздел дискретной математики и как раздел алгебры. Матрицы широко используются и при обработке результатов психологических экспериментов (в первую очередь это матрица первичных данных и корреляционная матрица)

Методические рекомендации

Прочитайте текст лекции, выполните упражнения. Рассмотрите различные способы решения системы линейных уравнений. Обратите внимание на условия совместности системы линейных уравнений.

Литература

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Часть I «Линейная алгебра» Глава 1 «Линейные уравнения. Идеи и примеры» (стр.12-30), глава 2 «Линейные уравнения» (стр.30-51), глава 3»Векторы и матрицы» (стр 51-61)

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава XVIII «Определители второго и третьего порядка» (стр. 307-324)

Дополнительно

Д.К.Фаддеев «Лекции по алгебре» Глава V «Матрицы и определители» (стр. 72-142)

Контрольные вопросы:

1. Что такое матрица? Что определяют два нижних индекса ее элементов?

2. Какие бывают матрицы? Приведите примеры

3. Какие действия можно выполнять над матрицами?

4. Что такое определитель квадратной матрицы?

5. Доказать, что слагаемых-произведений, входящих в формулу определителя, отличающихся одно от другого набором элементов существует ровно n!

6. Докажите, что определитель треугольной матрицы равен произведению элементов главной диагонали

7. Если матрицы А и В можно умножать, следует ли из этого, что их можно складывать? Если матрицы А и В можно складывать, следует ли из этого, что их можно умножать?

Можно ли умножить квадратную матрицу на неквадратную? Может ли произведение неквадратных матриц быть квадратной матрицей?

8. Может ли при умножении ненулевых матриц получиться нулевая матрица?

9. Могут ли совпадать матрицы А и АТ?

10. Опишите 3 способа решения систем линейных уравнений (метод определителей (Крамера), метод Гаусса и метод обратных матриц)

11. Решите тремя способами систему

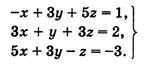
12. Решите уравнение

9. Сформулируйте и докажите свойства обратных матриц

Матрицы. Действия над матрицами

Рассмотрим неориентированный граф (рис. 5.1(1)), вершины которого являются, скажем, городами, а ребра – дорогами. Из города (1) можно попасть в без пересадки только в город (2), из (2) – в (1), (3) и (4), из (3) можно доехать в (2) и (4), а из (4) – в (2) и (3)

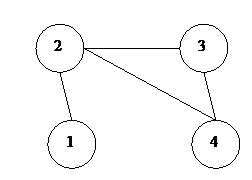
Рис.5.1(1)

Составим таблицу достижимости городов за одну поездку: «0» - отсутствие дороги, 1 – ее наличие (таб. 5.1(1)). Строки соответствуют городам, столбцы – концам дорог. Нетрудно видеть, что сумма чисел в строке соответствует степени соответствующей вершины графа

Города	(1)	(2)	(3)	(4)
(1)
(2)
(3)
(4)

Таблица 5.1(1)

Положение каждого числа в этой таблице характеризуется двумя показателями – строкой(городом) и столбцом (концом выходящей дороги). Так, например, числа третьей строки характеризуются парой «координат»: 0 – 3-1; 1 – 3-2; 0 – 3-3; 1 – 3-4

(Данная таблица симметрична относительно главной диагонали в силу неориентированности графа. В случае ориентированного графа матрица, вообще говоря, таковой может и не быть)

Рассмотрим теперь подобную таблицу общего вида (см.таб.5.1(2)). В клетках таблицы могут стоять любые числа, но каждое характеризуется по-прежнему двумя координатами – номером строки и столбца. Элемент некоторой клетки обозначается прописной латинской буквой с двумя нижними индексами – «адресами элемента» : a_ij – элемент i –й строки и j-го столбца

Столбцы Строки	(1)	(2)	…	(n)
(1)	a11	a12	…	a1n
(2)	a21	a22	…	a2n
…	…	…	…	…
(m)	am1	am2	…	amn

Таблица 5.1(2)

Определения 5.1(1)

Матрицей А размера m 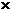n называется прямоугольная таблица из m строк и n столбцов, состоящая из чисел или иных математических выражений a_ij –(называемых элементами матрицы), i = 1,2,...,m, j = 1,2,. ..,n. Матрицы обозначаются заглавными латинскими буквами, сама таблица берется в круглые скобки.

С другой стороны , для положительных целых чисел m и n матрицей m 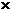n, или массивом m 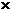n, называется функция

A: {1,2,…,m} 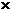{1,2,…,n}→ D

где D — это, как правило, множество действительных, комплексных, рациональных или целых чисел.

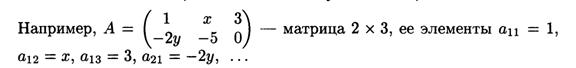
Главная диагональ матрицы– диагональ из левого верхнего в правый нижний угол ее элементы имеют вид a_ii

Квадратной матрицей n-го порядка называется матрица размера n х n.

Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали (т. е. с индексами i≠ j) равны нулю.

Единичной (обозначается Е) называется диагональная матрица с единицами на главной диагонали.

Нулевой называется матрица, все элементы которой равны нулю.

Треугольная матрица – матрица, у которой по главной диагонали и выше(ниже) нее идут ненулевые элементы, а все остальные равны нулю.

Ступенчатой называется матрица, состоящая из квадратных матриц, часть из которых – по главной диагонали и выше(ниже) ненулевые, а остальные – нулевые.

(«образующих ступеньку»)

Определение 5.1(2)

Две матрицы одинаковой размерности m ´ n называются равными, если в них одинаковые места заняты одними и теми же элементами (на пересечении i-й строки и j-го столбца в одной и в другой матрице стоит тот же элеменгт; i=1, 2, ..., m; j=1, 2, ..., n).

Примеры 5.1.

1)квадратная матрица 3х3

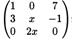
2)диагональная матрица

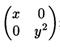
3)единичная

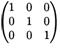
4)нулевая

5)ступенчатая

(А О)

В С , где А, В и С – квадратные матрицы, О – квадрат из нулей

Еще один вариант определения матрицы – это таблица коэффициентов системы (линейных) уравнений

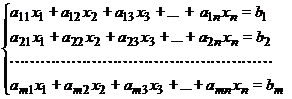
И система эта в матричной записи выглядит следующим образом:

AX = B, где А – матрица коэффициентов, Х – столбец неизвестных, а В – столбец свободных членов (об умножении матриц см.далее):

;

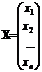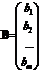
Замечание 5.1.

Для произвольной матрицы элементы а_ij