Вынужденные колебания систем с произвольным числом

Степеней свободы при действии вибрационной нагрузки

Рассматриваем установившиеся вынужденные колебания системы (рис.14.4) без учета внешнего или внутреннего сопротив­ления. Будем считать, что внешнюю нагрузку можно разложить по направлениям перемещений сосредоточенных масс, а составляю­щие ее обозначим , (i = 1,2,3,...,n).

Рис.14.4

Таким образом, роль внешних сил здесь будут играть величины:

. (14.22)

Канонические уравнения метода сил в данном случае записы­ваются в виде:

(r = 1,2,3,...,n). (14.23)

Подставляя (14.22) в (14.23) и после ряда преобразова­ний, получим:

(i = 1,2,3,...,n). (14.24)

Здесь - амплитудное значение перемещения i-ой массы, вызванное действием системы внешних сил .

Частное решение системы уравнений (14.24) записывается в виде:

, (14.25)

где - амплитуда перемещения i-ой массы; - частота вынуж­денных колебаний системы.

Выражение для определения инерционных сил принимает вид:

Z_i (t) = , (14.26)

где - амплитудные величины инерционных сил.

Принимая обозначение

(14.27)

и с учетом (14.26) систему уравнений можно преобразовать к сле­дующему виду:

(14.28)

решение которого записывается в виде:

. (14.29)

Здесь D и D_i - соответственно, определитель системы (14.28) и определитель, полученный из D заменой элементов 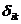(k = 1,2,..., n) соответствующими свободными членами (i = 1,2,..., n), т.е.

;

. (14.30)

Нетрудно заметить, что определитель D совпадает по форме с выражением (14.19), и поэтому при , т.е. при стремлении зна­чения частоты вынужденных колебаний к частоте собственных ко­лебаний заданной системы, получим , следовательно и соответственно, и согласно (14.26) , т.е. будет иметь место резонанс.

График зависимости от частоты имеет вид, приведенный на рис.14.5.

Рис.14.5

Однако увеличение амплитуды колебаний при резонансе до бесконечности является абстракцией. В действительности всегда имеются контуры, ограничивающие величину амплитуды , в частности внутреннее трение материала конструкции или внешнее сопротивление. Поэтому в действительности при происходит значительное увеличение , при этом оставаясь конечной величи­ной.

После определения из (14.29) с учетом (14.22) следует опре­делить амплитудное значение внешних сил:

,(i = 1, 2,..., n), (14.31)

и по значениям (i = 1, 2,..., n) определить амплитудное значе­ние внутренних усилий.

Например, общее выражение для определения амплитудных значений изгибающих моментов от динамических сил R_i (t) для статически неопределимых систем можно записать в виде:

,

где M_ik (k,i = 1,2,..., n) - значение момента в i-ом сечении при действии единичной силы в точке k.

НАЗАД НА ОГЛАВЛЕНИЕ ДАЛЕЕ

Главная/Лекции/Расчетно-графические работы/Расчеты строительных конструкций на ЭВМ/Зачетные вопросы/Справочные данные/Литература

Пример динамического расчета рамы

На раме с размерами, указанными на рис.14.6, в точках 1 и 2 установлены два одинаковых вибратора весом G = 20 кН каждый и весом неуравновешенных частей Р₀ =1,2 кН, размещенные на оси вращения с эксцентриситетом е = 0,015 м. Вибраторы вращаются синфазно с частотой n = 600 об/мин.

Рама выполнена из двух двутавров № 50 (ГОСТ 8239-72), т.е. J_x = 3,29×10^-4 м⁴; W_x =0,157×10^{-2 м3}. Рама изготовлена из стали с харак­теристиками Е = 2,1×10⁵ МПа, R = 190 МПа.

Пренебрегая собственным весом рамы и внутренним трением мате­риала, требуется:

1. Составить канонические урав­нения по методу сил, определяющие свободные колебания рамы, и полу­чить значения частот и периодов соб­ственных колебаний рамы;

2. Вычислить отношения ампли­туд и графически изобразить возможные формы собственных ко­лебаний рамы;

3. Проверить ортогональность собственных форм колебаний си­стемы;

4. Определить круговую частоту вынужденных колебаний и изо­бразить примерный вид графика коэффициента динамичности;

5. Составить канонические уравнения по методу сил, определя­ющие вынужденные колебания системы, и определить амплитуд­ные значения инерционных сил;

6. Построить статическую эпюру изгибающих моментов от всех вибраторов и эпюру амплитудных значений изгибающих моментов при вынужденном режиме колебания рамы;

7. Построить эпюру моментов при одновременном действии статических и динамических сил и определить положение опасного сечения конструкции;

8. Вычислить максимальное значение напряжения в опасном сечении и проверить условия прочности для принятого поперечно­го сечения рамы.

Решение:

Расчетная схема рассматриваемой системы показана на рис.14.6. Под действием периодической возмущающей нагрузки рама совер­шает колебательное движение.

Рис.14.6

Пренебрегая внутренним трением материала рамы и ее собственным весом, упругие перемещения сечений 1 и 2 по принципу независимости действия сил записы­ваются в виде:

(14.32)

где 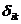- перемещение i-ого сечения от статической единичной силы, приложенной в k-ом сечении (i = 1,2; k = 1,2) по направле­нию соответствующей инерционной силы; , - перемеще­ния сечений 1 и 2 от всех динамических нагрузок. При этом:

(14.33)

где

(14.34)

С учетом выражений (14.33) и (14.34) и m₁ = m₂ = m уравнение (14.32) в стационарном режиме колебаний можно переписать в виде:

(14.35)

где .

Решая систему уравнений (14.35) определяют амплитудные зна­чения инерционных нагрузок (способом Крамера):

, (i = 1,2), (14.36)

где приняты следующие обозначения:

.

Учитывая, что в данном случае P₁ = P₂, амплитуды динами­ческого прогиба и изгибающего момента в произвольном i-ом (i = 1,2,...) сечении могут быть определены по формулам:

(14.37)

Уравнения движения (14.32) при свободных колебаниях рамы, т.е. при P₁ = P₂ = 0, принимают вид

(14.38)

Относительно амплитуды перемещения последняя система уравнений преобразуется в виде:

(14.39)

где .

Здесь 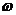- частота собственных колебаний рамы.

Система алгебраических уравнений (14.39) относительно ампли­туды перемещения сосредоточенных масс имеет различные реше­ния. Очевидное решение свидетельствует об отсутст­вии движения системы и не подходит по смыслу поставленной задачи.

Система (14.39) может иметь решения, отличные от нулевого, лишь в том случае, когда ее определитель равен нулю, т.е. когда выполняется условие:

. (14.40)

Раскрыв определитель (14.40), получим квадратное уравнение относительно . После определения с учетом (14.39) вычисляются собственные частоты .

Первая частота называется частотой основного тона собст­венных колебаний. Каждой частоте соответствует определенная форма колебаний системы. Форму колебания можно изобразить графически. Для этого в уравнения (14.39) следует подставить зна­чение (i = 1, 2), причем:

. (14.41)

При этом одно из двух уравнений (14.39) становится лишним. Пренебрегая первым уравнением (14.39), из второго получим:

, (i = 1,2). (14.42)

После чего, задавая значение y_ii (i = 1,2), можно вычислить в долях , а - в долях и изобразить графический характер возможной формы колебаний первого и второго тона колебаний.

Формы колебаний должны быть ортогональны. Условие ортого­нальности собственных форм записывается в виде:

, (r,k = 1,2; r ¹ k). (14.43)

Определив собственные частоты и и вычислив частоту вынужденных колебаний , необходимо сопоставить с ближай­шей из или . Во избежание наступления резонансных колеба­ний рекомендуется, чтобы отличалась от любой из частот , не менее чем на 30%. Если при решении задачи окажется, что это требование не выполняется, то следует изменить значение или . Этого можно достичь путем:

- изменения геометрических или физико-механических характеристик материалов элементов рамы;

- уменьшения или увеличения частоты вращения вибратора.

При этом во всех случаях напряжения в опасных сечениях ра­мы должны удовлетворять условиям прочности.

Переходим к численной реализации решения в соответствии с постановкой задачи.

1. Определение частот и периодов собственных колебаний рассматриваемой системы

Предварительно определим изгибную жесткость элементов заданной системы:

кН×м².

Заданная система один раз статически неопределима. Основная система метода сил представлена на рис.14.7, а. Эпюра моментов в основной системе от действия силы Х₁ = 1 показана на рис.14.7, б, а от единичных внешних сил - на рис.14.8, а, б.

Сначала рассчитываем раму на действие силы . Канони­ческое уравнение метода сил в данном случае записывается в виде:

. (14.44)

Рис.14.7

Рис.14.8

Коэффициенты и находим перемножением эпюр и по формуле Мора.

Здесь определяется как результат перемножения эпюры (рис.14.7, б) самой на себя, как результат перемножения эпюры (рис.14.7, б) с (рис.14.8, а).

(14.45)

С учетом (14.45) из решения (14.44) получим:

.

Эпюра изгибающих моментов в заданной системе от действия сил Р₁ =1 и Х₁ = 5/16 изображена на рис.14.9, a.

Рис.14.9

Рассчитываем раму на действие силы Р₂ = 1. Каноническое уравнение метода сил в данном случае принимает вид:

. (14.46)

Здесь определяется как результат перемножения эпюры моментов, изображенных на рис.14.7, б и 14.8, б, в соответствии с формулой Мора:

. (14.47)

С учетом значения из (14.45) и значения из (14.47) и из (14.46) получим:

.

Эпюра изгибающих моментов от действия сил Р₂ = 1 и Х₁ = = 7/4 в заданной системе изображена на рис.14.9, б.

Единичное перемещение 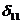определяется по формуле Мора в результате перемножения эпюры самой на себя, применяя формулы умножения двух эпюр моментов в виде двух трапеций на произвольном участке. Получим:

м/кН.

Единичное перемещение определяется по формуле Мора перемножением эпюры самой на себя (рис.14.9, б):

м/кН.

Единичное перемещение определяется по формуле Мора в результате перемножения эпюр и , изображенных соот­ветственно на рис.14.9, а, б:

м/кН.

Решив уравнение (14.40), получим:

,

откуда

.

Окончательно =166,75×10^-6 м/кН; =10,.35×10^-6 м/кН.

По формуле (14.41) определяется значение собственной частоты рассматриваемой рамы:

c^-1;

c^-1.

Периоды собственных колебаний рассматриваемой системы принимают значения: c; c.

2. Определение амплитуды собственных колебаний и графическое изображение собственных форм

Для вычисления значения отношений амплитуды собственных колебаний из (14.42), предварительно определив кН∙с²/м, имеем при = 1 и при = 1, соответственно:

Формы собственных колебаний рассматриваемой системы изо­бражены на рис.14.10 (а - первая форма; б - вторая форма).

3. Проверка ортогональности собственных форм колебаний

Из условия ортогональности (14.43) имеем:

.

Рис.14.10

4. Определение круговой частоты вынужденных колебаний и изображение примерного вида графика коэффициента динамичности в зависимости от отношения частот вынужденных и собственных колебаний

В стационарном режиме круговая частота вынужденных колеба­ний системы имеет значение:

c^-1.

Сопоставим величину с величиной ближайшей собственной частоты рамы :

.

Во избежание резонансных колебаний надо изменить величину или . В данном случае, принимая n = 900 об/мин, получим:

c^-1;

,

Рис.14.11

Следовательно, при с^-1 при­нятое условие во избежание резонансных колебаний выполняется.

Примерный вид графика коэффици­ента динамичности в зависимости от изображен на рис. 14.11.

5. Определение амплитудных значений инерционных сил

В соответствии с принятым обозначением по формулам (14.34) и (14.35) последовательно определяем:

м/кН;

м/кН;

кН;

м/кН;

м/кН;

м²/кН;

м²/кН;

м²/кН.

По (14.33) определяем амплитудные значения инерционных сил:

= |D₁/D |= |3,72/0.5| = 7,44 кН;

= |D₂/D |= |9,64/0.5 |= 19,28 кН.

6. Определение эпюры изгибающих моментов от действия собственного веса вибраторов и амплитудных значений изгибающих моментов при вынужденном стационарном режиме колебания рамы

Значение изгибающих моментов, возникающих от действия собственного веса вибраторов, в произвольном сечении опреде­ляется по формуле:

.

Определяем значение в характерных сечениях (0; 1; 2; 3) рамы (см. рис.14.9):

сечение 0: = 20×(9/8 - 3/2) = -7,5 кН×м;

сечение 1: = 20×(-15/16 + 3/4) = -3,75 кН×м;

сечение 2: = 0;

сечение 3: = 20×(0 + 3) = 60 кН×м.

Эпюра изгибающих моментов приведена на рис.14.12.

Амплитудные значения изгибающих моментов от действия внешних динамических и инерци­онных нагрузок в соответствии с (14.37) определяются:

=

.

Рис. 14.12

Согласно последней формуле в характерных сечениях имеет

следующие значения:

сечение 0: кН×м;

сечение 1: кН×м;

сечение 2: = 0;

сечение 3: кН×м.

Эпюра изображена на рис.14.12 (пунктиром).

7. Построить эпюру моментов при одновременном действии статических и динамических сил и определить положение опасного сечения конструкции

Результирующее значение изгибающих моментов, действующих в характерных сечениях при одновременном действии статических и динамических нагрузок, определяется по формуле:

.

Эпюра M_k, как и эпюры и , изображены на рис.14.12.

Из рис.14.12 согласно эпюре М следует, что наиболее опасным яв­ляется сечение 3.

8. Определение максимального напряжения и проверка условий прочности в наиболее опасном сечении

кН/м² = 53,2МПа <R = 190 МПа.

Следовательно, условие прочности рассматриваемой рамы обес­печено.

НАЗАД НА ОГЛАВЛЕНИЕ ДАЛЕЕ

Главная/Лекции/Расчетно-графические работы/Расчеты строительных конструкций на ЭВМ/Зачетные вопросы/Справочные данные/Литература