Современный методический подход к вопросу обучения решению задач

Лекция 14

Тема. ПОДГОТОВКА ДОШКОЛЬНИКОВ К ОБУЧЕНИЮ РЕШЕНИЮ ЗАДАЧ

ПЛАН

1. Современный методический подход к вопросу обучения решению задач.

2. Задача как математическое понятие.

3. Подготовительная работа к обучению решению задач.

4. Примерные разработки занятий по подготовке и обуче­нию решению задач детей старшей и подготовительной групп.

Вопросы:

1. Раскройте современный подход к решению дошкольниками задач.

2. Почему «задача» - это математическое понятие?

3. Раскройте содержание подготовительной работы к решению задач.

Задания для самостоятельного выполнения

1. Подобрать 5 задач на сложение и вычитание.

Литература:

1. Белошистая А. В.Формирование и развитие математических способно­стей дошкольников: Вопросы теории и практики: Курс лек­ций для студ. дошк. факультетов высш. учеб. заведений. — М.: Гуманит. изд. центр ВЛАДОС, 2003. — С. 84 – 97.

Современный методический подход к вопросу обучения решению задач

Обучение решению задач является сложнейшей методической проблемой не только в методике обучения математик! младших школьников, но и в методике обучения математики в старших классах.

Методические подходы к вопросу о порядке изучения арифметических действий, вычислений и обучения решению задач значительно изменились за последние 15-20 лет, что обусловлено главным образом упрочением позиций развивающего обучения и личностно-деятельностного подхода к пониманию цели и сути образовательного процесса. Общепринятые сегодня в системе развивающего обучения подход состоит в том, что знакомить ребенка с арифметическими действиями и соответственно с простейшими приемами вычислений следует раньше, чем начинать обучение решению задач.

В связи с этим необходимость обучения дошкольников решению задач вызывает большое сомнение с методической точки зрения, поскольку в условиях дошкольной подготовки сложно решить все аспекты этой методической проблемы.

Задача как математическое понятие присутствует сегодня и в традиционной программе математической подготовки дошкольников, в программах «Радуга» и «Детство», которые опираются в этом вопросе на традиционную методику пособия А.М. Леушиной, но ее нет в программе «Школа 2000», авторы которой впервые знакомят ребенка с задачей в конце первого полугодия 1 класса.

Таким образом, налицо противоречие между тем методическим подходом к процессу обучения, который был принят в 70-е годы, когда было написано пособие А.М. Леушиной, и современным пониманием роли и места задач в обучении ребенка математике. В учебных пособиях по математике нового поколении (учебники И.И. Аргинской и учебники Н.Б. Истоминой), созданных для устанавливающейся сейчас системы двенадцатилетней школы с четырехлетним начальным звеном, тема «Задача» вообще не рассматривается в 1 классе, предусмотрена только подготовительная работа к знакомству с этим понятием, а с задачами как таковыми дети знакомятся во 2 классе.

При рассмотрении задачи как вербальной (текстовой) структуры принято выделять ее характерные признаки: условие, вопрос, данные, искомое.

В текстах стандартной формы условие выражено повествовательным предложением и предшествует вопросу, который выражен вопросительным предложением.

К нетиповым относятся тексты, в которых или требован и. выражено повествовательным предложением, или вся задачи сформулирована одним предложением, или условие разделить на две части и т. п.

Например:

1) В гараже стояли 2 легковые и 5 грузовых машин. Найти количество машин в гараже.

2) Сколько карандашей было у Маши, если 3 карандаша он отдала брату, а 4 оставила себе?

3) На полке стояло 6 книг. Сколько книг осталось на полки после того, как 2 книги Петя отнес в библиотеку? и т. п.

Нетиповые тексты могут быть построены и на других принципах — это могут быть тексты с нехваткой или излишком данного.

Например:

1) На дереве сидели птицы. 5 из них — это воробьи, остальные — голуби. Сколько было голубей?

2) В вазе лежало 8 апельсинов. Ваня съел 2 апельсина, и Катя съела 3 апельсина. Сколько апельсинов они съели?

Работа с такими текстами является наиболее полезной с точки зрения обучения решению задач, поскольку именно такие тексты учат ребенка внимательно читать и анализировать задачу, целенаправленно устанавливать связи между данными и искомым с целью осознанного выбора действия.

Безусловно, при отсутствии умения читать такую работу ребенок осуществить не может. Если же предлагать такую работу ребенку, плохо читающему, то на практике мы обычно наблюдаем в этом случае подмену работы над текстом задачи мани­пулированием числовыми данными. Это происходит потому, что числовые данные, обозначенные цифрами, бросаются в гла­за при небольшом тексте в первую очередь. Поскольку в тек­сте стандартной задачи в 1 классе обычно бывает два число­вых данных, с которыми нужно выполнить арифметическое действие (сложение или вычитание), ребенок, плохо читаю­щий, просто выполняет с выделенными числовыми данными знакомое арифметическое действие (наугад). Если же учитель не подтверждает правильность выбора действия, то достаточно выполнить другое из двух известных действий.

В результате подобной практики формируется достаточно распространен­ный стереотип действий ребенка с задачей, когда он выполня­ет действия с числами, заданными текстом задачи, даже не за­думываясь над смыслом этих действий и результатом.

Противоположный способ работы над задачей можно наблю­дать в практике работы воспитателя ДОУ при раннем знаком­стве с задачей, когда педагог, зная что дети не могут работать с текстом самостоятельно, старается облегчить им восприятие этого текста, моделируя все его числовые компоненты на на­глядности. (Хотя именно числовые компоненты воспринима­ются ребенком быстрее и легче всего.)

При этом на столе или фланелеграфе выставляется все нужное количество предметов и перед глазами детей выполняются все обозначенные услови­ем действия.

Например:

Задача. 6 мартышек сидели на ветке. Одна — свалилась. Сколько мартышек осталось на ветке?

Иллюстрируя этот текст, педагог его, выставляет на флане­леграф изображения шести мартышек, затем снимает одну мартышку и ставит ее несколько в стороне или снимает с фланелеграфа. Остальные пять остаются перед глазами детей. При такой организации наглядности не только процесс ре­шения задачи теряет смысл, но и способ получения результа­та совершенно противоположен тому, который предполагает­ся при решении задачи.

Ответ при решении задачи должен быть получен как результат выполнения арифметического действия (!).

При описанном выше способе работы с наглядностью ребе­нок не только не озабочен выбором действия, но и не должен его выполнять, поскольку ответ он может получить пе­ресчетом. При ответе на вопрос, какое действие он выполнял, ребенок ориентируется на действие учителя (снял мартышку — надо отнимать) или на слово (отдали, унесли, съели, осталось и т. п. — надо вычитать, дали, купили, стало, вместе и т. ш надо складывать).

При работе со стандартными формулировками и просты текстами такой прием некоторое время выручает и ребенка и педагога. Однако первый же нестандартный текст покажет порочность такого метода работы при обучении решению задач.

Например:

1) Из бочки вылили сначала 5 ведер воды, а потом еще 2 ведра. Сколько ведер воды вылили? (Типичной ошибкой является действие: 5 — 2.)

2) У Вани и Пети вместе было 7 шариков. Сколько шариков было у Вани, если у Пети было 3 шарика? (Типичная ошибка 7 + 3 или, в лучшем случае, 3 + 4.)

Занятие 1

Тема занятия. Подготовка к знакомству с задачей.

Цель занятия. Познакомить детей со схемой ситуации. Научить читать схему ситуации.

Упражнение 1 Цель. Развивать зрительное внимание, тренировать наблюдатель­ность, формировать умение производить анализ. Материалы. Рисунок на доске. Задание. — Какие фигуры вы видите на рисунках: а)

Упражнение 2 Цель. Уметь моделировать ситуацию задачи на предметной нагляд­ности. Материалы. Рисунок на доске или предметная модель на фланеле­графе.

Задание. На халате 10 петель. Мама пришила 4 пуговицы. Сосчитайте, сколько еще надо пуговиц. Для выполнения задания обозначьте приши­тые пуговицы кружками.

оооо

Упражнение 3

Цель. Уметь моделировать ситуацию задачи, воспринятой «на слух».

Материалы. Счетные палочки.

Задание.

А. На дворе гуляли 3 курицы. Положите перед собой на столе столько палочек, сколько у них ног. Сосчитайте, сколько ног?

Б. Потом на двор вышли кошка и собака. Положите столько палочек, сколько у них ног. Сколько ног у кошки, у собаки? Сосчитайте, сколько ног на дворе.

В. А потом к ним в гости пришел слон. Добавьте столько палочек, сколь­ко ног у слона. Сколько теперь ног на дворе?

Г. К обеду в гости пришел удав. Сколько теперь ног на дворе? (Ног ос­талось столько же, сколько было, потому что у удава нет ног.)

Упражнение 4

Цель. Повторить состав однозначных чисел в процессе моделирова­ния ситуации задачи.

Материалы. «Дидактический набор» или набор «Учись считать».

Способ выполнения. Все задания дети моделируют фигурками из на­бора и отвечают на вопросы, ориентируясь на свою модель.

Задание. Мартышка наводила в доме порядок и расставляла на окнах цветы. В комнате два окна.

А. Как она могла расставить 4 горшка? (1 и 3, 2 и 2, 3 и 1, 4 и О.)

Б. Как она могла расставить 6 горшков на 2 окна поровну? Сколько на каждом?

В. Один горшок она уронила за окно. Сколько их осталось? (5) Как рас­ставить оставшиеся горшки на два окна поровну? {Нельзя, один лишний.)

Упражнение 5

Цель. Моделировать ситуацию задачи на схеме. Материалы. Рисунок на доске или схема из карточек и стрелок на фла­нелеграфе.

Задание.У Мартышки день рождения. Чтобы не забыть, что нужно сделать, она попросила Попугая нарисовать ей план — что поставить на стол. Попугай нарисовал такой план:

Что это может означать? Где у Попугая обозначены полки с посудой, а где — стол? (3 чашки с одной полки и 1 чашку с другой полки поставили на стол. На столе стоит 4 чашки.)

Упражнение 6

Цель. Моделировать ситуацию задачи на схеме. Материалы. Рисунок на доске или схема из карточек и стрелок на фла­нелеграфе.

Задание.Пришли гости — Удав и Слоненок. А потом с чашками кое-что произош­ло. Попугай нарисовал такую картинку:

Что могло произойти, что тут изображено? (Было 4 чашки. Две чашки унесли на кухню, две — осталось. Или: две — разбили, две — осталось.)

Примечание. Легко видеть, что стрелки на схеме моделируют направ­ление и вид действия. Сходящиеся стрелки моделируют объединение, де­ти их обычно так и воспринимают.Расходящиеся стрелки — удаление час­ти. На данной схеме не задано однозначно, какая часть удалена, а какая оставлена. Пока это несущественно. В дальнейшем, когда один из эле­ментов схемы заменится на знак вопроса, т. е. произойдет переход к струк­туре «задача», станет однозначно понятно, что удалили и что надо найти.

Направление движения стрелок полезно показать руками, чтобы дети осознавали смысл схемы, моделируя ее через собственную кинестетику (движения рук).

Упражнение 7

Цель. Закреплять умение составлять схему ситуации. Материалы. Фланелеграф, карточки с цифрами и стрелки из бархат­ной бумаги.

Способ выполнения. Дети составляют сюжетный рассказ и изобража­ют его с помощью схемы.

Задание. Составить схему по этим картинкам:

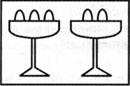
Как обозначить на схеме, что здесь произошло?

Рассказ может быть, например, таким: «Было 3 яблока и 2 яблока в двух вазах. Их сложили в одну вазу. В ней стало 5 яблок». Схема выгля­дит следующим образом:

Примечание. Педагог обращает внимание на то, что это пока не за­дача, а рассказ с числами. Нет нужды вводить в такой рассказ вопрос.

Упражнение 8

Цель. Составлять рассказ по схеме (задание обратное предыдущему). Материалы. Фланелеграф, карточки с цифрами, стрелки.

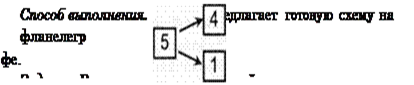. Рассказ может быть, например, таким: У Мартышки было 5 горшков с цветами. Один она уронила за окно. Осталось 4.

Другой вариант: У Мартышки было 5 бананов. 4 она съела, а одни угостила Слоненка.

Упражнение 9

Цель. Закреплять умение составлять выражения и схемы по рисунку. Материалы. Рисунки ситуаций задач.

Задание. Составить записи по рисункам и рассказы по картинкам. Ко всем рисункам можно составлять схемы.

Занятие 2

Упражнение 2

Цель. Закреплять умение составлять выражения по предметной мо­дели ситуации.

Упражнение 3

Цель. Учить соотносить схематическую и символическую (матема­тическое выражение) модель ситуации.

Материалы. На доске или фланелеграфе заранее сложено несколько схем.

Способ выполнения. Дети выбирают схемы, соответствующие выра­жениям из предыдущего упражнения.

Задание. Выбрать из данных схем подходящую к первому выражению, объяснить свой выбор и зарисовать ее в тетради (дети рисуют простым карандашом «от руки»).

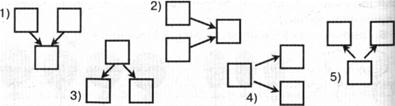
Примечание. Критерий выбора — направление стрелок. К сумме под­ходит первая и вторая схема, остальные три подходят только к разности. Последовательность действий следующая: сначала выбирается нужная по структуре схема. Затем в нее вставляются исходные числа: пустые кар­точки просто заменяются на карточки с цифрами. Последним заполняется «окошко», в котором надо подсчитать результат.

Например. Для выражения 6 + 2 подходит первая схема:

В ней стрелки показывают, что два числа надо соединить, собрать вме­сте, сложить. Чтобы заполнить последнее окошко, надо сосчитать фигур­ки. Их 8. Значит:

Для выражения 7-1 подходит третья схема. Стрелки показывают, что надо что-то отделить, убрать, отнять. Отнимали от 7, значит:

Чтобы заполнить третье окошко, надо сосчитать, сколько кружков ос­талось. Их 6. Значит,

Педагог помогает детям сформулировать объяснение. Подсказывает правильные термины: сумма, складывать, отнять, вычесть, разность.

Упражнение 4

Цель. Учить детей соотносить сюжетный рассказ со схемой. Материалы. Рисунок на доске или схема на фланелеграфе. Задание. Составить рассказы по схемам:

Если дети затрудняются в выборе сюжета, педагог подсказывает им: про Мартышку, про магазин, про кукол и т. п. Используя карточки с цифра­ми, дети заполняют окошки.

Примечание. Данные упражнения легко осваиваются детьми и выпол­няются без всякого труда, поскольку воспринимаются как игра.

Упражнение 5

Цель. Закреплять умение соотносить сюжетный рассказ со схемой. Материалы. Рисунки ситуаций задач.

Задание. Составлять записи по рисункам и уметь рассказывать по кар­тинкам. Ко всем рисункам можно составлять схемы.

Занятие 3

Тема занятия. Математическое равенство.

Цель занятия. Обобщать представление о смысле знака равенст Познакомить со знаком сравнения и неравенством.

Упражнение 1

Цель. Уметь быть внимательным, тренировать наблюдательность, рай вивать умение анализировать.

Материалы. Рисунок на доске. Х'^ч^чЗ

Задание. Какие фигуры вы видите на рисунке? Сколь­ко треугольников спряталось в рисунке?

Упражнение 2

Цель. Учить детей соотносить сюжетный рассказ со схемой. Материалы. Рисунки на доске или модели на фланелеграфе.

Задание. На полянке расцвело 6 ромашек

— Девочка сорвала 2 ромашки, осталось 4. Составьте выражение (6 -

— Какая схема из этих двух подходит к этому выражению?

Как ее заполнить?

— Что означает число 6 в схеме? (Эти ромашки были сначала.) Что оз­начает число 2? (Эти ромашки сорвали.) Что означает число 4? (Эти ро- I машки остались.) Сравните запись 6 - 2 и схему. (В записи не обозначено число 4.)

— В схеме мы обозначили число оставшихся ромашек, а в записи вы­ражения — не обозначили. Можно продолжить эту запись и обозначить число оставшихся ромашек, для этого используют специальный знак. Его называют «знак равенства». Пишут так: 6-2 = 4.

— Говорят так: от 6 отнять 2 равняется 4.

— Всю эту запись целиком называют: «равенство» — по имени знака равенства, который в ней использован.

— Послушайте рассказ: на ветке сидели 3 воробья и 2 голубя. Составьте выражение (3+2). Сосчитайте на пальцах, сколько всего птиц? Дополните

запись до равенства (3 + 2 = 5). Прочитайте ее. (КЗ прибавить 2равня­ется 5.)

Упражнение 3

Цель. Закреплять представление о равенстве. Познакомить с понятия­ми верное и неверное равенство.

Материалы. Лист на печатной основе.

Способ выполнения. Работа на печатном листе.

Задание.

А. Среди выражений 4 + 1; 3 - 1 =2; 5 + 2 = 6; 7-1 подчеркните все равенства красным карандашом. Все ли они верные? Как вы понимаете это слово? Почему равенство 5 + 2 = 6 —неверное? Исправьте ошибки (зачеркните неверный ответ и напишите рядом верный). Проверьте себя на пальцах или на палочках.

Б. Вставьте число в пропуски так, чтобы равенство было верным:

2 + ...=3 3 + ... = 5 2+...=6

5-...=4 4-... = 2 5+...=6

В. Вставьте нужное число в схему, чтобы она была верной:

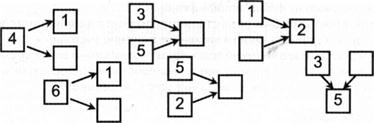
Упражнение 4

Цель. Знакомить со знаком сравнения. Материалы. Счетные палочки.

Задание. Назвать два любых соседних числа. На сколько отличаются два соседних числа? (На 1.) Докажите это: постройте на палочках модели двух соседних чисел (любых, каждый свою пару). Разложите палочки так, чтобы я сразу увидела, что одно больше другого на 1.

— Для того чтобы записать в тетради, что одно число больше другого, используют специальный значок — знак сравнения: < — острым концом этот знак всегда показывает на то число, которое меньше.

Педагог предлагает детям выходить к фланелеграфу и сравнивать любые предлагаемые ими числа. Для моделирования знака сравнения ис­пользуют две маленькие полоски бархатной бумаги.

При этом педагог показывает детям возможность двух прочтений зна­ка без изменения его положения:

— Запись 6 < 8 можно прочитать: шесть меньше восьми или восемь больше шести.

Упражнение 5

Цель. Учить сравнивать числа с использованием знака сравнения.

Способ выполнения. Предыдущее задание выполняется в обратной последовательности: сначала ставится знак, а дети должны подобрать со­ответствующую пару чисел: ...>... и ...<...

Упражнение 6

Цель. Обучать постановке знака сравнения между выражениями. Материалы. Рисунок на доске или карточки с цифрами и фланелеграф. Способ выполнения. Педагог организует беседу.Вариант беседы.

— Мы сравнивали числа, используя знак сравнения. Как вы думаете, можно ли использовать этот знак для сравнения числа и выражения? Пе­дагог составлет на фланелеграфе запись: 4+1 ... 4.

Чтобы поставить знак равенства или сравнения в записях такого вида, необходимо сравнить число и численное значение выражения. При этом в данном случае его не нужно подсчитывать, достаточно сослаться на то, что сумма 4 и 1 будет больше, чем только одно число 4. Воспитатель зна­комит детей с названием записи такого вида: неравенство.

Упражнение 7

Цель. Закрепление умения сравнивать выражения и записывать ре­зультат с помощью знака.

Задание. Сравнить числа и выражения. (Используются задания на сравнение чисел и выражений.)

Занятие 4

Тема занятия. Задача.

Цель занятия. Знакомить с понятием «задача». Упражнение 1

Цель. Формировать умение различать выражения с разными знаками действий (умственная операция классификация). Знакомить с названия­ми выражений.

Материалы. На фланелеграфе или на доске карточки с записями. Задание. Разделить на две группы эти записи:

3+2 6-2 3-1 2+3

7-1 5-2 4+2 6-3

Способ выполнения. Таблички с записями дети сортируют в зависи­мости от того, стоит там знак «+» или знак «-».

3+2 7-1

4+2 6-2

2+3 5-2

3-1 6-3

— Как назвать выражения в первом столбике? Во втором?

Эти названия дети еще не знают и обычно предлагают названия, свя­занные со знаками сложения и вычитания: «складывание», «вычитание», «отнимание». Педагог сообщает новые слова: сумма и разность.

Упражнение 2

Цель. Формировать вычислительные умения.

Материалы. Печатные листы с теми же записями и в том же порядке, как на доске.

Задание. Найти ответ и записать его, дополнив запись до равенства. Результаты обсуждаются и проверяются на палочках, на пальцах.

Упражнение 3

Цель. Закреплять умение составлять рассказ по схеме. Материалы. Рисунок на доске или схема на фланелеграфе. Задание. Составить рассказ по схеме:

Упражнение 4

Цель. Знакомить со схемой задачи.

Материалы. Рисунок на доске или схема на фланелеграфе.

— Чем этот рассказ будет отличаться от предыдущего? (В схеме есть знак вопроса, значит, заканчивать рассказ надо вопросом.)

Педагог сообщает, что рассказ, заканчивающийся вопросом, отвечая на который, надо выполнить какое-то действие (прибавить или отнять), называется задачей.

Примечание. Данное определение весьма приблизительно сформу­лировано в понятной детям форме и не предназначено для заучивания.

Упражнение 5

Цель. Уточнять правильное понимание особенностей задачи. Способ выполнения. Педагог организует беседу. Вариант беседы.

—То, что рассказал Ваня, — это задача. Можем мы ответить на ее во­прос? (Да.) То, что рассказала Таня —- это задача. Можем мы ответить на ее вопрос? (Да.)

—А теперь послушайте меня и скажите, можно ли назвать задачей фра­зу: «Два конца, два кольца — посередине гвоздик». Что это? (Это не зада­ча, а загадка.)

—Чем отличается задача от загадки? (В загадке надо догадаться, а в задаче — выполнить действие.)

—Хорошо, тогда придумайте задачу вы. (Обсуждается вариант, пред­лагаемый детьми. Отвечаем на вопрос.)

—А кто знает загадку с числами?

— Послушайте меня: У стола 4 ножки, по 2 с каждой стороны, Но сапожки и калошки этим ножкам не нужны.

Это — задача? (Нет, это стишок, в котором нет вопроса.)

— Послушайте еще: Два березовых коня По снегам несут меня. Кони эти рыжи,

А зовут их... (Лыжи! Это не задача, а загадка.)

— Чем же задача отличается от загадки?

Педагог подводит детей к пониманию того, что в задаче предлагается проблемная ситуация, для разрешения которой надо выбрать арифме­тическое действие и затем, выполнив его, ответить на вопрос.

Упражнение 6

Цель. Уточнять представление о признаках задачи. Материалы. Коробка с красными и зелеными карандашами. Способ выполнения. Беседа, сопровождаемая предметными дейст­виями.

Вариант беседы.

— Послушайте такую задачу: Мальчик положил в коробку красные и зеленые карандаши. Сколько там карандашей? (На этот вопрос отве­тить нельзя. Надо знать, сколько было красных и зеленых карандашей.)

Педагог приглашает ребенка к столу, дает ему пустую коробку и каран­даши. На глазах у детей он отсчитывает: кладу 5 красных (кладет их в ко­робку, и они детям уже не видны) и 2 зеленых карандаша (кладет их в ту же коробку и закрывает ее).

— Кто составит схему?

Дети составляют схему на фланелеграфе, используя карточки с чис­лами и стрелки:

— Почему стрелки сходятся вместе? (Все карандаши в одной короб­ке.) Что на схеме обозначает коробку с карандашами? (Кружок со знаком «?») Как составить выражение по этой схеме? Какой знак,«+» или«-», нужно использовать? (Знак «+», так как все карандаши вместе в одной коробке. Запись: 5 + 2.)

— Какой же вопрос в задаче? (Сколько карандашей в коробке?) Можно ли на него ответить? Сосчитайте. Дополните запись до равенства: 5 + 2 = 7.

— Проверим, правильно ли мы нашли ответ.

— Петя, иди посчитай карандаши в коробке. Сколько их? (7) Правиль­но мы решили задачу? (Да.)

— Если бы я спросила: «Какие карандаши в коробке?», а не «Сколько карандашей в коробке?», тогда получилась бы задача? Почему нет? (Что­бы ответить на первый вопрос, не надо выполнять действие.)

Примечание. Конечно, дети не смогут так четко сразу обосновать от­вет, педагог помогает им наводящими вопросами.

Упражнение 7

Цель. Закреплять умение составлять разные выражения к одной к л тинке и объяснять их.

Материалы. Рисунок и записи на доске:

3 + 2 3-2 5-3

2+3 5-2 5+1

4+1 4-1 4+2

Задание. Из данных записей выбрать те, что подходят к картинке. Обьяснить свой выбор.

Примечание. Дети легко выбирают и объясняют записи 3 + 2 и 2 + 3 (два треугольника и три кружка), но выбор записи 5 - 2 и 5 — 3 иногда приходится подсказать: всего 5 фигур, из них 2 треугольника и т. п.

Занятие 5

Тема занятия. Задача.

Цель занятия. Учить детей составлять схему и запись решения про­стой задачи на нахождение суммы и остатка.

Упражнение 1

Цель. Уточнять представление о признаках задачи. Способ выполнения. Беседа с учащимися. Вариант беседы. Педагог читает детям тексты:

У стола четыре ножки.

Ну, а сколько лап у кошки?

Столько ж, сколько у кота,

Все четыре — мягкота.

— Это — задача? (Это — стишок.)

Этот конь не ест овса,

Вместо ног два колеса.

Сядь верхом и мчись на нем,

Только лучше правь рулем!

— Это — задача? (Это — загадка. Велосипед.)

Стала курица считать

Маленьких цыпляток:

Желтых — пять

И черных — пять...

— Закончите стишок так, чтобы получилась задача. Как ответить на вопрос задачи? Составьте равенство в наборном полотне. Проверьте от­вет на палочках.

Упражнение 2

Цель. Учить составлять схему задачи.

Материалы. Фланелеграф, карточки с цифрами и стрелки, счетные па­лочки, касса цифр (наборное полотно).

Способ выполнения. Беседа, сопровождаемая составлением схем. Вариант беседы.

— Мартышка нашла на грядке 4 спелых клубники и 2 зеленых. Подели­лась она с Попугаем? Это задача? (Это не задача, так как мы не можем ответить на вопрос, выполнив какое-то действие.)

— Измените вопрос так, чтобы получилась задача. (Сколько ягод она нашла?)

— Составьте схему на фланелеграфе.

— Составьте выражение в наборном полотне. Почему вы взяли знак сложения? Найдите ответ и проверьте его на папочках.

Упражнение 3

Цель. Учить составлять схему задачи.

Вариант беседы. Удав нюхал цветы на поляне. Всего там расцвело 7 цветов. Пришел Слоненок и нечаянно наступил на один цветок. Сколько цветов теперь сможет понюхать Слоненок?

— Это задача? (Да.) Составьте схему на фланелеграфе:

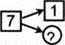
— Составьте запись в наборном полотне. Почему надо отнимать 1? (Слоненок наступил, поэтому цветов стало меньше. Стрелкой показали, что один цветок из семи пропал.) Найдите ответ.

Упражнение 4

Цель. Учить анализировать текст задачи. Способ выполнения. Беседа.

Вариант беседы. У Мартышки 3 банана. Если она поделится с Попуга­ем, сколько достанется каждому? (Здесь разные ответы: 2 и 1, а если «по-честному», то 1 и еще половинка). Это задача? (Задача, но в ней не хвата­ет данных, чтобы получить точный ответ.)

— А если Удав тоже захочет получить банан, тогда по скольку доста­нется каждому? (Тогда всем по 1, потому что их трое и бананов — 3.) Будет ли этот ответ единственным? (Если делить честно, то единственный.)

Упражнение 5

Цель. Учить анализировать числовые данные задачи. Материалы. Фланелеграф, бумажные модели предметов, счетные пи .почки.

Способ выполнения. Беседа, сопровождаемая предметными деиствиями.

Вариант беседы. Педагог выставляет на фланелеграф изображении 6 бананов.

— А если у Мартышки 6 бананов и она поделится с Попугаем, то ско/и, ко каждому может достаться?

Дети выходят к фланелеграфу и раскладывают бананы, повторяя оо| став числа 6 (5 и 1, 2 и 4, 3 и 3).

— А если делить по-честному? (3 и 3). А если еще Слоненку оставин. и всем поровну? (2, 2 и 2)

— А если Удав тоже захочет банан, тогда что делать, как делить поров« ну? (Всем по одному, а оставшиеся 2 банана разрезать пополам и всей дать еще по половинке.) Сколько же будет у каждого? (7 и еще половинка,)

Примечание. Эти рассуждения надо обязательно сопровождать прак­тической работой. Удобно использовать спички со снятой головкой, так как их не жалко ломать при делении пополам и распределении половин. Такие задания являются пропедевтикой (подготовкой восприятия) поня­тий: деление с остатком и без остатка, дробь и доля.

Упражнение 6

Цель. Закреплять вычислительные умения и умения переводить рисо­ванную модель в символическую.

Материалы. Печатный лист с заданиями.

Способ выполнения. Работа с печатным листом.

Задание. Дополнить записи, чтобы равенства стали верными:

1 +...=3 3 + ...=4 ...+6 = 7

4-1 =... 5-1 =... ...-1 = 1

0 + 2 = .... 8-... = 7 5+... = 5

Примечание. Все равенства дети дополняют, используя присчитыва­ние или отсчитывание и свойства нуля.

Задание. Подчеркнуть запись, соответствующую рисунку:

4-1 3+1 3-1

2 + 2 4-2 4-3

Задание. Нарисовать к каждой записи картинку по образцу:

8 + 2= 10

8+ 1 + 1 =...

В заключение приведем пример занятия по ознакомлению детей с не­стандартными текстами задач.

Занятие 6

Упражнение 1

Цель. Актуализировать знания детей о временах года и названиях ме­сяцев, днях недели, календаре.

Материалы. Большой календарь. Чтобы детям легче было находить нужные месяцы, возле каждого можно приклеить картинки из старых на­стенных календарей, помогающие визуально найти нужное время года и нужный месяц.

Способ выполнения. Работа с календарем.

Задания. Какой сегодня день? Какое число? Какой месяц? Найдите его на календаре.

— Какой месяц следующий? Какое время года начнется? Какое закон­чится? Каким днем недели является 1 июля? 1 июня? 1 августа? 1 сентяб­ря? 31 декабря? Какой по счету месяц — декабрь?

Упражнение 2

Цель. Уточнять представление о задаче. Материалы. Календарь. Способ выполнения. Беседа. Вариант беседы.

— Мартышка насчитала в ноябре 4 субботы, а воскресений — на 1 боль­ше. Сколько было воскресений?

— Можно назвать это задачей? (Да.) Выложите столько зеленых пал»ии. сколько было суббот, а красных палочек столько, сколько было воскресений Сколько воскресений? (5) Почему 5? (Потому, что на 1 больше, чем суббот.)

Упражнение 3

Цель. Уточнять представление о задаче. Материалы. Счетные палочки.

Задание. Мартышка насчитала 4 субботы и 5 воскресений в ноябре, Поставьте вопрос, чтобы получилась задача. (Сколько выходных в нояб­ре?) Ответьте на вопрос. Проверьте себя на палочках.

Упражнение 4

Цель. Знакомить с нестандартными текстами задач. Задания.

А. Попугай сказал Мартышке: «У меня есть бананы. Два я съем, а ос­тавшийся банан отдам тебе. Угадай, сколько у меня бананов?»

— Как составить запись решения к этой задаче?

Задачу полезно разыграть: педагог за Попугая прячет за спиной «ба­наны», не позволяя детям сосчитать исходное количество. Два банана от­даются одному ребенку, теперь их можно сосчитать. У педагога остается один банан.

— Что надо сделать, чтобы узнать, сколько бананов было сначала? (Нужно их сложить, тогда узнаем, сколько их было сначала.)

Запись: 2 + 1=3.

Б. У мухи 6 ног, а у слона — 4. У кого больше? На сколько?

— Поставьте красных палочек столько, сколько ног у мухи, а зеленых столько, сколько ног у слона. Какой ответ у задачи? У кого ног меньше? На сколько? У кого ног больше? На сколько?

Запись к этой задаче составлять не надо, поскольку задача решена пе­ресчетом.

Примечание. Такой способ решения задач на разностное сравнение на данном этапе достаточен. Базой для их решения служит умение срав­нивать множества способом взаимно однозначного соответствия. Запись решения этого типа задач (запись действия) дети освоят во 2 полугодии 1 класса четырехлетней начальной школы (в традиционной программе). Задачи этого типа следует рассматривать только после длительного и хорошо организованного пропедевтического периода, поскольку обе формулировки вопроса «на сколько больше» и «на сколько меньше» пред­полагают действие вычитания в решении задачи. Для осознания этого фак­та ребенок должен опираться на правильную модель ситуации.

В. На блюде лежат 10 апельсинов. (Модель блюда и апельсинов на столе у педагога.) Незнайка съел 3 апельсина (кто-то из детей ассистирует пе­дагогу, складывая в корзинку «съеденные» апельсины, чтобы ответ не мог быть получен пересчетом). Гунька съел 4 апельсина. Сколько апельсинов они съели?

— Как это узнать? Составьте запись в кассе. Помните, сколько апель­синов съел каждый? Сколько апельсинов они съели вместе?

Педагог дает детям возможность самостоятельно составить запись ре­шения, а затем проводит анализ результатов.

— Почему выбрали действие сложения? (Все «съеденные» апельсины лежат в корзине, это помогает детям правильно выбрать действие.) Что означает каждое число в записи? Какое число в условии задачи вам не понадобилось для ее решения? (10)

— Можно ли так поставить вопрос к этой задаче, чтобы это число по­надобилось для решения? (Сколько апельсинов осталось?)

— Какое действие нужно выполнить для ответа на этот вопрос? Запи­шите его. (10-6 = 4)

Примечание. Задачи такого вида называют задачами с излишком дан­ных. Такие задачи полезны для формирования умения внимательно изучать текст задачи и анализировать его на предмет необходимости и достаточности данных. Эти задачи удобны для подготовки к появлению в перспективе составных задач, поскольку второй вопрос к такому тексту позволяет задействовать «лишнее» данное и выполнить еще одно дейст­вие (фактически решить задачу в два действия). После записи действия полезно выполнить проверку — сосчитать апельсины в корзине.

Г. Потом пришел Буратино и съел еще несколько апельсинов. Сколько апельсинов осталось?

Дети замечают, что на вопрос ответить нельзя. Такие тексты называют «задачи с недостатком данных». Они используются для того, чтобы дети учились анализировать текст.

— Почему нельзя ответить на вопрос? Что вам нужно знать, чтобы на него ответить? (Сколько именно он съел.) Предположим, он съел 1 апель­син? (3) Если он съел 2? (2) Съел 3? (1)

—А как вы думаете, сколько он съел? (Скорее всего он съел все, значит, не осталось ни одного.)

Приведенные тексты четырех занятий представляют собой взаимосвязанный блок, поскольку в них последовательно рас­смотрены взаимосвязанные понятия.

Лекция 14

Тема. ПОДГОТОВКА ДОШКОЛЬНИКОВ К ОБУЧЕНИЮ РЕШЕНИЮ ЗАДАЧ

ПЛАН

1. Современный методический подхо