Математического и пружинного маятника

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

МАТЕМАТИЧЕСКОГО и ПРУЖИННОГО МАЯТНИКА

Ознакомьтесь с конспектом лекций и учебником. Запустите программу. Выберите «Механика», «Механические колебания и волны» и «Свободные колебания» (сначала математический маятник, потом груз на пружине). Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ еще раз.)

ЦЕЛЬ РАБОТЫ:

* Выбор физических моделей для анализа движения тел.

* Исследование движения тела под действием квазиупругой силы.

* Экспериментальное определение зависимости частоты колебаний от параметров системы.

КРАТКАЯ ТЕОРИЯ:

КОЛЕБАНИЕ – периодически повторяющееся движения тела. ПЕРИОД T – минимальное время, через которое движение полностью повторяется.

ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ – движение, при котором координата тела меняется со временем по закону синуса или косинуса: .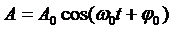

Основными характеристиками гармонических колебаний являются:

АМПЛИТУДА А₀ – максимальное значение параметра А.

ЦИКЛИЧЕСКАЯ ЧАСТОТА собственных колебаний w₀ – в 2p раз большая обычной или линейной частоты n = 1/Т (n – число полных колебаний за единицу времени).

ФАЗА (w₀t + j₀) – значение аргумента косинуса.

НАЧАЛЬНАЯ ФАЗА j₀ – значение аргумента косинуса при t = 0.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных гармонических колебаний параметра А: 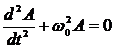, свободных затухающих колебаний:

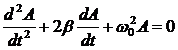, где b – коэффициент затухания.

МАТЕМАТИЧЕСКИЙ МАЯТНИК (ММ) и ПРУЖИННЫЙ МАЯТНИК (ПМ) – это МОДЕЛИ объектов, в которых могут происходить гармонические колебания.

МАТЕМАТИЧЕСКИЙ МАЯТНИК – это материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити.

ПРУЖИННЫЙ МАЯТНИК – это материальная точка, прикрепленная к идеальной (невесомой и подчиняющейся закону Гука) пружине. Формулы для w₀ в этих системах выпишите из конспекта или учебника.

ЗАДАНИЕ: Выведите формулу для циклической частоты свободных колебаний кубика на пружине, лежащего на горизонтальной абсолютно гладкой поверхности.

УКАЗАНИЯ: Выпишите формулу для второго закона Ньютона. Подставьте в нее все реальные силы, действующие на кубик. Спроектируйте полученное векторное уравнение на вертикальную и горизонтальную оси. Проведя тождественные преобразования, получите уравнение, похожее на дифференциальное уравнение свободных колебаний. Константу, являющуюся множителем перед А, приравняйте к квадрату циклической частоты, откуда получите w.

ЭКСПЕРИМЕНТ 1

Выберите «Маятник». Установите с помощью движков управления параметрами максимальную длину нити L и значения коэффициента затухания и начального угла, указанные в табл. 1 для вашей бригады.

Таблица 1. Значения коэффициента затухания (вязкого трения), начального угла отклонения (для первого эксперимента) и начального отклонения (для второго).

Номер бригады	b, кг/с	j0, град	X0, см	m, кг	Номер бригады	b, кг/с	j0, град	X0, см	m, кг
	0.10			0.5		0.50			0.7
	0.15			0.6		0.55			0.8
	0.20			0.7		0.60			0.9
	0.25			0.8		0.70			1.0
	0.30			0.7		0.80			0,5
	0.35			0.8		0.90			0,6
	0.40			0.9		1,00			0,7
	0.45			1.0		1.20			0,8

Нажимая мышью на кнопку «СТАРТ», следите за движением точки на графиках угла и скорости и за поведением маятника. Потренируйтесь, останавливая движение кнопкой «СТОП» (например, в максимуме смещения) и запуская далее кнопкой «СТАРТ». Выберите число полных колебаний N =3–5 и измеряйте их продолжительность Dt (как разность t₂ – t₁ из таблицы на экране).

Таблица 2. Результаты измерений (количество измерений и строк – 8)

Номер измерения	N =
L, м	Dt, с	Т, с	Т2,с2
	1,5
	1,4
	1,3
	1,2
...	0,8
g, м/с2

ЭКСПЕРИМЕНТ 2

Выберите макет «Груз на пружине». Установите массу груза, значение коэффициента затухания и начальное смещение, указанные в табл. 1 для вашей бригады.

2) Проведите измерения, аналогичные эксперименту 1, уменьшая коэффициент жесткости k каждый раз на 1 Н/м.Результаты внесите в табл.3

Таблица 3. Результаты измерений (количество измерений и строк – 6)

Номер измерения	N =
k, H/м	Dt, с	Т, с	w,1/с	w2,1/с2
...

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:

Вычислите требуемые величины и заполните таблицы 2 и 3.

Постройте графики зависимости:

· квадрата периода колебаний Т² = f(L) от длины нити ММ,

· квадрата циклической частоты колебаний w² = f(k) от жесткости пружины ПМ.

По наклону графика Т² = f(L) определите значение g, используя формулу

g =4p ² 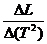. Оцените абсолютную ошибку определения g.

По наклону графика w² = f(k) определите значение m, используя формулу

m = 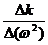. Оцените абсолютную ошибку определения m.

Проанализируйте ответ и графики.

Вопросы и задания для самоконтроля

1. Что такое колебание?

2. Дайте определение периода колебаний.

3. Дайте определение частоты колебаний.

4. Дайте определение гармонических колебаний.

5. Запишите закон зависимости от времени характеристики А, совершающей гармоническое колебательное изменение.

6. Запишите закон движения материальной точки (МТ), совершающей гармонические колебания.

7. Дайте определение амплитуды гармонических колебаний.

8. Дайте определение фазы гармонических колебаний.

9. Дайте определение начальной фазы гармонических колебаний.

10. Напишите уравнение связи частоты и периода гармонических колебаний.

11. Напишите уравнение связи частоты и циклической частоты гармонических колебаний.

12. Напишите формулу зависимости скорости МТ от времени при гармонических колебаниях.

13. Напишите уравнения связи амплитуды скорости и амплитуды смещения при гармонических колебаниях МТ.

14. Напишите формулу зависимости ускорения МТ от времени при гармонических колебаниях.

15. Напишите уравнения связи амплитуды скорости и амплитуды ускорения при гармонических колебаниях МТ.

16. Напишите уравнения связи амплитуды смещения и амплитуды ускорения при гармонических колебаниях МТ.

17. Напишите дифференциальное уравнение свободных гармонических колебаний МТ.

18. Напишите дифференциальное уравнение свободных затухающих колебаний МТ.

19. Что определяет коэффициент затухания?

20. Дайте определение математического маятника.

21. Запишите формулу циклической частоты свободных колебаний математического маятника.

22. Дайте определение пружинного маятника.

23. Запишите формулу циклической частоты свободных колебаний пружинного маятника.

24. Какие процессы происходят при вынужденных колебаниях?

25. Что такое резонанс?

26. При каком затухании резонанс будет более резким?

ЛАБОРАТОРНАЯ РАБОТА № ТК-3

ЦЕЛЬ РАБОТЫ:

* Знакомство с компьютерной моделью процесса свободных затухающих колебаний в электрическом колебательном контуре.

* Экспериментальное исследование закономерностей свободных затухающих колебаний.

* Экспериментальное определение величины индуктивности контура.

КРАТКАЯ ТЕОРИЯ:

КОЛЕБАТЕЛЬНЫМ КОНТУРОМ называется замкнутая цепь, содержащая катушку индуктивности с индуктивностью L и конденсатор с емкостью С. Если в цепи нет активного сопротивления R (резистора), то в контуре возможны гармонические (незатухающие) колебания тока I, заряда конденсатора q и напряжения на элементах.

НАПРЯЖЕНИЕ НА КОНДЕНСАТОРЕ: .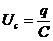

ЭДС самоиндукции в катушке: .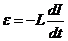

НАПРЯЖЕНИЕ НА РЕЗИСТОРЕ: .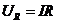

ОПРЕДЕЛЕНИЕ ТОКА: .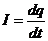

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных незатухающих колебаний:

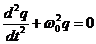, где w₀ = 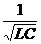– собственная частота контура .

Период: Т = 2p .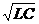

Его решение q(t) = q_v cos(w₀ t + a), где a – начальная фаза.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных затухающих колебаний

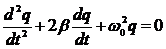, где b = 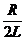– коэффициент затухания.

Его решение: q(t) = q_v0 е^-bt cos(wt + a), где 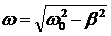– частота затухающих колебаний.

ПОСТОЯННАЯ ВРЕМЕНИ ЗАТУХАНИЯ в контуре t есть время, за которое амплитуда колебаний уменьшается в е = 2,73 раз. На графике зависимости амплитуды затухающих колебаний от времени касательная, проведенная к этому графику в начальный момент времени, пересекает ось времени в точке t = t.

q(t)

А₁

А₂ ---- касательная

А₃

t

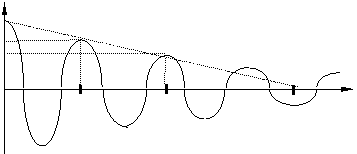t

t₂ = Т t₃ = 2Т

ЛОГАРИФМИЧЕСКИМ ДЕКРЕМЕНТНОМ ЗАТУХАНИЯ называется величина, определяемая формулой 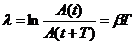. ДОБРОТНОСТЬ контура равна Q = .

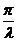ТАБЛИЦА 1. Значения емкости конденсатора и индуктивности катушки

Бригада
С, мкФ			2,7	2,7	2,4	2,4
L, мГн
Бригада
С, мкФ			2,7	2,7	2,4	2,4
L, мГн

1) Установите сопротивления резистора R = 1 Ом. Нажав кнопку «Старт», наблюдайте график зависимости заряда конденсатора от времени. Измерьте линейкой значения первых шести амплитуд и запишите их в табл. 2

Меняя сопротивление R, повторите измерения амплитуд и заполните таблицу 2.

ТАБЛИЦА 2. Результаты измерений при С = ____ мкФ, L = ____ мГн,

Т = ____ мс.

R Ом	А1 мм	А2 мм	А3 мм	А4 мм	А5 мм	А6 мм	t мс	b с-1
t, мс

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:

Рассчитайте значения периода колебаний и запишите в заголовке табл. 2.

Рассчитайте время t, при котором измерена соответствующая амплитуда и запишите в табл. 2.

Постройте на одном чертеже графики экспериментальных зависимостей амплитуды колебания А от времени t (6 линий, соответствующих разным R).

Для каждого графика постройте касательную к нему в начальный момент времени. Продолжив касательную до пересечения с осью времени, определите экспериментальное значение постоянной времени затухания t и запишите в табл. 2.

Рассчитайте величины коэффициента затухания b = 1/t и также внесите в табл. 2.

Постройте график зависимости коэффициента затухания от сопротивления резистора.

По графику b(R) определите индуктивность контура, используя формулу .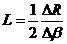

Запишите ответ и сформулируйте выводы по ответу и графикам.

Вопросы и задания для самоконтроля

1. Что такое колебательный контур?

2. Каковы электрические характеристики резистора, конденсатора, катушки?

3. Дайте определение гармонических колебаний.

4. Что такое период колебания?

5. Какая физическая величина испытывает колебания в колебательном контуре?

6. Напишите формулу для напряжения на конденсаторе.

7. Напишите формулу для напряжения на катушке индуктивности. Какое другое название она имеет?

8. Напишите формулу для напряжения на резисторе. Какое другое название она имеет?

9. Какие законы выполняются для тока и напряжения на отдельных элементах в колебательном контуре?

10. Сформулируйте и запишите в виде формулы закон электромагнитной индукции в общем виде.

11. Сформулируйте и запишите в виде формулы закон электромагнитной индукции для проводящего контура.

12. Сформулируйте и запишите в виде формулы закон самоиндукции.

13. Запишите дифференциальное уравнение для заряда на конденсаторе в контуре, где существуют свободные гармонические колебания.

14. Запишите дифференциальное уравнение для заряда на конденсаторе в контуре, где существуют свободные затухающие колебания.

15. Напишите формулу циклической частоты свободных гармонических колебаний в контуре.

16. Напишите формулу зависимости заряда на конденсаторе от времени при свободных гармонических колебаниях в контуре.

17. Напишите формулу циклической частоты свободных затухающих колебаний в контуре.

18. Напишите формулу зависимости заряда на конденсаторе от времени при свободных затухающих колебаниях в контуре.

19. Напишите формулу для коэффициента затухания.

20. Дайте определение постоянной времени затухания.

21. Напишите формулу логарифмического декремента затухания. Что он характеризует?

22. Напишите формулу связи логарифмического декремента затухания с коэффициентом затухания.

23. Напишите формулу для добротности контура. Что определяет добротность?

24. Нарисуйте зависимость заряда на конденсаторе от времени при свободных затухающих колебаниях в контуре. Покажите на рисунке, как определяется графически постоянная времени затухания.

ЛАБОРАТОРНАЯ РАБОТА ТК-4

ЦЕЛЬ РАБОТЫ

* Знакомство с компьютерным моделированием процессов в колебательном RLC-контуре.

* Экспериментальное подтверждение закономерностей при вынужденных колебаниях в RLC-контуре.

КРАТКАЯ ТЕОРИЯ

Повторите основные определения для колебательного движения, которые приведены в ЛР 1_4. Прочитайте также снова теорию к ЛР 2_3, в которой рассмотрены свободные колебания в контуре.

ВЫНУЖДЕННЫМИ КОЛЕБАНИЯМИ называются процессы, происходящие в контуре, содержащем конденсатор, катушку индуктивности, резистор и источник с переменной ЭДС, включенные последовательно и образующие замкнутую электрическую цепь.

Если ЭДС источника меняется по гармоническому закону, то в контуре наблюдаются вынужденные гармонические колебания. При этом ток в контуре также будет переменным, подчиняющимся закону Ома в комплексной форме.

КОМПЛЕКСНАЯ ВЕЛИЧИНА есть определенная совокупность двух алгебраических чисел 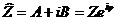, где А – действительная часть, В – мнимая часть, Z – модуль, j – фаза комплексной величины. Графически 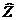изображается, как радиус-вектор на комплексной плоскости: его длина равна Z, а угол между вектором и горизонтальной (действительной) осью равен j.

КОМПЛЕКСНЫЙ ТОК и КОМПЛЕКСНОЕ НАПРЯЖЕНИЕ

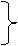
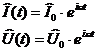– это векторы, которые вращаются с угловой скоростью w.

Здесь 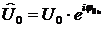– комплексная амплитуда напряжения;

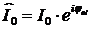– комплексная амплитуда тока.

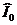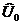и – комплексные векторы, которые на комплексной плоскости неподвижны. Они соответствуют «мгновенной фотографии» реальных комплексных токов и напряжений, сделанной в начальный момент времени (t = 0).

Комплексная амплитуда – сама комплексная величина, взятая в начальный момент времени.

Математически:

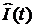
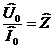(импеданс), Z

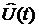
Импеданс – это отношение комплексной амплитуды напряжения на данном элементе, к комплексной амплитуде тока через данный элемент.

Модуль импеданса называется ПОЛНЫМ ЭЛЕКТРИЧЕСКИМ СОПРОТИВЛЕНИЕМ цепи.

;

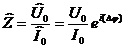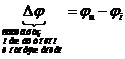
а) Резистор: 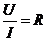; ; 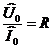фазы напряжения и тока одинаковые. Импеданс равен R: Z_R ≡ X_R = R .

б) Катушка индуктивности: Действует закон электромагнитной индукции (самоиндукции): .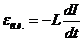

Использовав его и закон Ома для комплексных величин, получим:

;

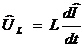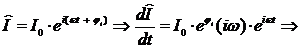
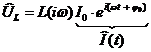
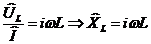– импеданс катушки индуктивности.

Напряжение на катушке опережает по фазе ток через нее на p/2.

в) Конденсатор: 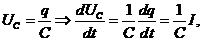или .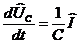

Пусть 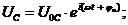тогда .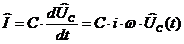

Найдем отношение 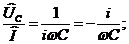отсюда

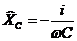– ­ комплексное сопротивление (импеданс) конденсатора.

Напряжение на конденсаторе отстает по фазе от тока через него на p/2.

Модуль комплексного сопротивления (катушки или конденсатора) называется РЕАКТИВНЫМ СОПРОТИВЛЕНИЕМ (индуктивным или емкостным). Обозначается символом без крышечки над ним.

Все элементы в контуре соединены последовательно, поэтому для нахождения импеданса контура надо просуммировать импедансы всех элементов:

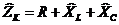. После подстановки можем получить модуль импеданса, то есть полное сопротивление контура:

.

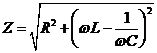РЕЗОНАНСОМ для тока называется явление резкого увеличения амплитуды колебаний тока при приближении частоты ЭДС к некоторому значению, называемому резонансной частотой w_РЕЗ . Нетрудно видеть, что максимум амплитуды тока будет тогда, когда минимально полное сопротивление контура, или Z_РЕЗ = R и 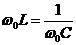, отсюда 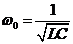, что соответствует частоте свободных колебаний в контуре.

Максимум напряжения на конденсаторе соответствует резонансу для напряжения, который наблюдается при несколько меньшей частоте ЭДС:

.

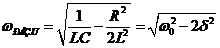d = 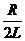– коэффициент затухания для данного контура.

Амплитуда резонансного напряжения на конденсаторе U_0C пропорциональна амплитуде ЭДС и добротности контура Q: U_0C = Q × e₀.

При не слишком большом затухании в контуре добротность определяется соотношением

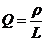, где r = 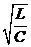называется характеристическим сопротивлением контура. Чем больше добротность, тем «острее» резонанс.

РЕЗОНАНСНОЙ КРИВОЙ называется зависимость амплитуды напряжения на конденсаторе от частоты ЭДС.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Закройте окно теории. Внимательно рассмотрите рисунок для компьютерной модели.

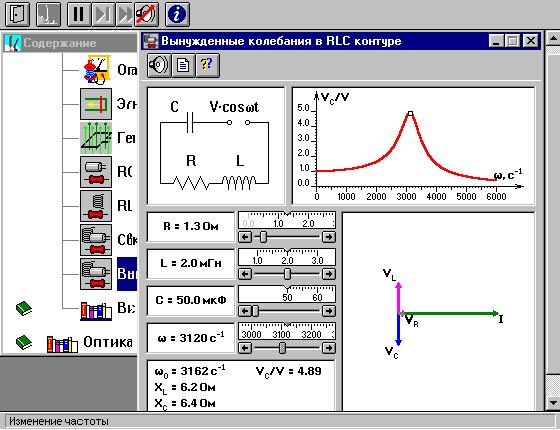
Перерисуйте необходимое в конспект, используя обозначения, принятые в нашей теоретической части (e₀ вместо V, U_0C вместо V_C , U_0L вместо V_L и U_0R вместо V_R).

Подготовьте табл. 1, используя образец. Подготовьте также табл. 3 и 4, аналогичные табл.1.

ТАБЛИЦА 1. результаты измерений (12 столбцов). L = ____ мГн	ТАБЛИЦА
	Бригады	R, Ом	L1, мГн	L2, мГн	L3, мГн		Бригады	R, Ом	L1, мГн	L2, мГн	L3, мГн
	1, 5	1 , 2	1,0	1,7	2,4		9 , 13	1, 2	1,0	1,7	2,4
	2, 6	2 ,1	1,2	1,9	2,6		10,14	2, 1	1,2	1,9	2,6
	3, 7	1 2	1,4	2,1	2,8		11,15	1, 2	1,4	2,1	2,8
	4 ,8	2, 1	1,6	2,3	3,0	12,16	2,1	1,6	2,3	3,0

C, мкФ =					...
wРЕЗ, 1/с
w0, 1/с
U0C/e0
1/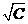

ЛАБОРАТОРНАЯ РАБОТА ТК № 5

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

При подготовке к лабораторной работе следует:

1. Повторить соответствующий теоретический материал, пользуясь конспектом лекций и рекомендованным Вам учебником физики.

2. Рекомендуется проделать на черновике вывод всех формул, особенно тех, что в пособии приведены без вывода.

3. Подготовить письменно краткие ответы на предлагаемые Вам «Вопросы для самоконтроля» (см. ниже).

4. Решить некоторые теоретические задачи из учебного пособия «Основы физики колебаний» (по индивидуальному заданию преподавателя).

5. Познакомиться с «Требованиями к оформлению отчета» о выполненной работе.

Задания и порядок выполнения лабораторной работы

1. Начните работу с раздела «Основы теории», в котором приведены краткие сведения об изучаемой физической системе и о соответствующей математической модели.

· Просмотрите последовательно все страницы этого раздела, запуская каждый раз (кнопкой «Пуск») моделирование соответствующих движений осциллятора.

· Особое внимание обратите на страницу, где обсуждается колебательный контур – электромагнитный аналог механического осциллятора.

2. Изучите колебания осциллятора в отсутствие трения.

· Выберите раздел «Графики колебаний» и откройте панель ввода параметров (либо нажатием кнопки «Ввод», либо выбрав пункт меню «Ввод данных») и снимите «галочку» в боксе «Вязкое трение». Введите некоторое начальное отклонение (скажем, 90 или 120 градусов) и нулевую начальную скорость. Закройте панель ввода, нажав кнопку «Ok».

· Начните моделирование, нажав кнопку «Пуск». Регулятором «Моделирование» установите временной масштаб, удобный для наблюдения». Обратите внимание на вид графиков угла отклонения и угловой скорости при выбранных начальных условиях. Какой математической функции соответствует каждый из графиков? Несколько раз приостановите моделирование кнопкой «Пауза» в разных фазах колебаний и сопоставьте наблюдаемое отклонение ротора с соответствующей точкой графика угла отклонения. Зарисуйте графики, обращая особое внимание на соотношение фаз колебаний угла отклонения и угловой скорости.

· Перейдите в раздел «Фазовая траектория». Обратите внимание на взаимное расположение окна фазовой траектории (в левом верхнем углу экрана) и осей на графиках зависимости от времени угла отклонения и угловой скорости. Выбранное расположение удобно для сопоставления движения изображающей точки по фазовой траектории с соответствующими точками на графиках временной зависимости переменных. Приостанавливая моделирование, проследите за одновременными положениями ротора на изображении и точек на всех графиках. Сопоставьте форму графиков и фазовой траектории колебаний в отсутствие трения.

· Перейдите в раздел «Превращения энергии». При моделировании колебаний обратите внимание на форму графиков потенциальной и кинетической энергий. Сопоставьте период колебаний угла отклонения с периодом колебаний потенциальной и кинетической энергий.

3. Изучите затухающие колебания осциллятора при вязком трении.

· На панели ввода параметров поставьте «галочку» в боксе «Вязкое трение» и введите некоторое значение добротности (5 – 20). Перейдите в раздел «Физическая система». Выполняя моделирование колебаний, занесите в таблицу серию значений последовательных максимальных отклонений ротора в одну сторону. Убедитесь в том, что эта последовательность представляет собой убывающую геометрическую прогрессию. Это можно сделать, вычисляя отношения последовательных отклонений – в случае геометрической прогрессии это отношение должно быть одним и тем же для любой пары последовательных членов. Сравните результат Ваших измерений с теоретическим значением этого отношения, рассчитанным для введенной Вами добротности.

· Перейдите в раздел «Фазовая траектория». При моделировании обратите внимание на форму графиков и фазовой траектории затухающих колебаний. Убедитесь, что по мере экспоненциального убывания амплитуды витки фазовой траектории становятся гуще, но условный период колебаний (т.е. промежуток времени между последовательными пересечениями оси абсцисс графиками) остается неизменным.

· Перейдите в раздел «Превращения энергии». Обратите внимание на характер графиков кинетической, потенциальной и полной энергии для затухающих колебаний – если за некоторое число циклов амплитуда уменьшается вдвое, то энергия за то же время уменьшается в четыре раза (убедитесь в этом).

· Сопоставьте поведение изображающей точки на фазовой плоскости с графиком зависимости полной энергии от угла отклонения – точка в потенциальной яме перемещается от одного берега к другому, достигая берегов ямы в точках поворота и постепенно опускаясь на ее дно.

· По поведению графика зависимости полной энергии от времени сделайте вывод о скорости рассеяния механической энергии на протяжении периода колебаний.

4. Промоделируйте движение осциллятора с критическим затуханием.

· Введите значение добротности, соответствующее критическому затуханию. Задайте начальные условия, соответствующие возбуждению осциллятора начальным толчком из положения равновесия.

· Откройте раздел «Фазовая траектория». Сравните наблюдаемую в этом случае фазовую траекторию и графики угла отклонения с соответствующими кривыми для случая слабого затухания. Оцените время, в течение которого осциллятор возвращается в положение равновесия при критическом затухании.

5. Проверьте в моделирующем эксперименте Ваши теоретические решения тех задач из учебного пособия, которые были Вам предложены преподавателем в качестве индивидуального задания.

· Введите необходимые значения параметров и выполните соответствующие эксперименты. Зарисуйте (или распечатайте на принтере) графики и фазовые диаграммы для включения в отчет.

· Сопоставьте результаты экспериментов с Вашими теоретическими предсказаниями. Если обнаруживаются расхождения результатов расчета с экспериментом, обязательно попытайтесь установить причину расхождений. Результаты экспериментальной проверки Ваших решений включите в отчет о лабораторной работе.

После выполнения всех заданий подготовьте отчет о проделанной лабораторной работе, руководствуясь «Требованиями к оформлению отчета».

Требования к оформлению отчета

Отчет о проделанной лабораторной работе должен содержать следующие разделы:

1. Титульный лист с указанием названия и номера лабораторной работы, фамилии и имени студента, номера учебной группы, даты выполнения работы и даты представления отчета.

2. Цель лабораторной работы с определением изучаемого физического явления и краткое описание моделируемой физической системы и ее математической модели.

3. Теоретический раздел с кратким изложением основных характеристик изучаемого явления, его места в классификации колебаний по разным признакам, и описанием математической модели физической системы, используемой для его изучения. В этом разделе должны быть приведены все основные формулы (связь параметров физической системы и ее математической модели, дифференциальное уравнение, описывающее систему, его общее решение, частные решения для наиболее важных и интересных случаев, уравнение фазовой траектории, выражения для разных видов энергии и их средних значений и т.п.). В этом разделе следует обязательно привести вывод тех формул, которые в учебном пособии приведены без вывода.

4. Ответы на вопросы для самоконтроля, которые сформулированы в «Методических рекомендациях» к данной лабораторной работе. Рекомендуется проиллюстрировать Ваши ответы соответствующими графиками или иными результатами моделирования (для тех вопросов, где это целесообразно).

5. Теоретическое решение задач из учебного пособия, предложенных Вам преподавателем в качестве индивидуального задания, и результаты самостоятельной проверки Ваших решений с помощью моделирующего эксперимента. В этом разделе нужно привести таблицы соответствующих измерений с обработкой результатов (для заданий, где такие измерения необходимы), графики и/или фазовые траектории (зарисовав их с экрана или распечатав на принтере, если есть такая возможность).

Вопросы для самоконтроля

1. Приведите несколько примеров физических систем, к которым применима модель линейного осциллятора. Опишите физическую систему (торсионный пружинный осциллятор), которая моделируется в лабораторной работе. Какими физическими параметрами характеризуется пружинный осциллятор?

2. Какие параметры характеризуют математическую модель осциллятора, используемую в лабораторной работе? Почему модель характеризуется меньшим числом параметров, чем моделируемая физическая система? Какими соотношениями параметры модели выражаются через параметры физической системы?

3. В каком случае состояние равновесия физической системы называется устойчивым? При каких условиях колебания системы около устойчивого равновесия называют собственными? Как можно возбудить собственные колебания?

4. При каких идеализациях свойств системы ее собственные колебания около устойчивого равновесия будут незатухающими? Как называются такие идеализированные системы?

5. Какой должна быть зависимость возвращающей силы от величины отклонения из равновесия, чтобы в отсутствие трения собственные колебания системы были гармоническими (синусоидальными)? Как потенциальная энергия в такой системе зависит от величины отклонения из равновесия?

6. Приведите вывод дифференциального уравнения гармонического осциллятора (в отсутствие трения) на примере таких систем, как груз на пружине и торсионный осциллятор, моделируемый в лабораторной работе. Как собственная частота линейного осциллятора выражается через физические параметры системы?

7. Как можно записать общее решение дифференциального уравнения гармонического осциллятора? Как найти значения произвольных постоянных в общем решении, если заданы начальные условия? Как амплитуда колебаний выражается через начальные условия?

8. Как период колебаний связан с собственной частотой? Зависят ли период, частота и амплитуда собственных колебаний от способа возбуждения колебаний (от начальных условий)? В чем заключается свойство изохронности линейного осциллятора?

9. Что такое фазовая траектория? Что за кривая соответствует фазовой траектории собственных колебаний линейного осциллятора? Как выглядит «фазовый портрет» (т.е. семейство фазовых траекторий, соответствующих разным значениям полной энергии) консервативного осциллятора?

10. В каком направлении движется вдоль фазовой траектории изображающая точка? Почему фазовая траектория собственных колебаний консервативного осциллятора представляет собой замкнутую кривую? В течение какого промежутка времени изображающая точка обходит фазовую траекторию?

11. Может ли одна и та же замкнутая фазовая траектория соответствовать колебаниям консервативного осциллятора, возбуждаемым при разных начальных условиях?

12. Какие превращения энергии происходят на протяжении одного цикла колебаний? С каким периодом и в каких пределах происходят колебания кинетической и потенциальной энергий консервативного осциллятора? Как энергия колебаний связана с амплитудой? Как изменится энергия колебаний, если амплитуду увеличить вдвое?

13. Как зависит от времени амплитуда собственных колебаний, затухающих под