Дифференциальное уравнение колебаний пружинного маятника в вязкой среде под действием внешней гармонической силы.
Я так понял это – резонанс из прошлого билета. Думаю надо рассказывать прошлый билет на этот вопрос.
28. Математический и физический маятники.
Математический маятник.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
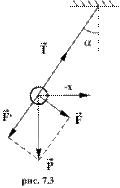
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 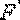 , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 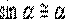 и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
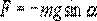
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
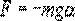
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 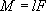 , и момент инерции:
, и момент инерции:
M = FL .
Момент инерции J в данном случае
Угловое ускорение:
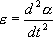
С учетом этих величин имеем:
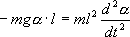
или
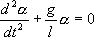
Его решение
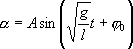 ,
,
где 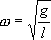 и
и 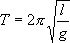
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Физический маятник.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
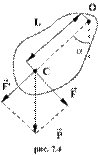
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
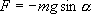
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
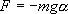
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
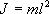 . Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
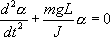
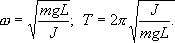
Решение этого уравнения
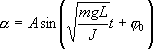
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. 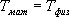 или
или
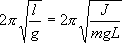 .
.
Из этого соотношения определяем
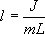
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
29. Сложение колебаний одного направления. Одинаковые частоты, биения.
Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача - найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний - нахождение траектории результирующего колебания.
Метод векторных диаграмм
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = wt + j0 где j0 - начальный угол.
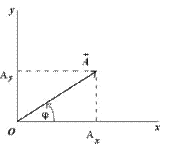
Проекции вектора А на оси координат запишутся:

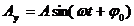
Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу - начальную фазу.
Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:
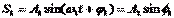
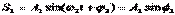
Сопоставим этим колебаниям два вектора А1 и А2, вращающихся с соответствующими угловыми скоростями.
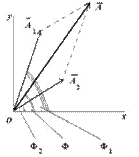
Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).
Из очевидных геометрических соображений находим:
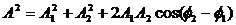
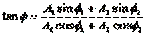
Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то 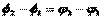 , то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:
, то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:
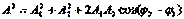
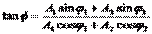
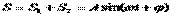
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть 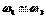 , и пусть для определенности
, и пусть для определенности 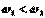 . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний
. Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний
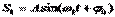

получим уравнение суммарного колебания:
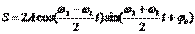
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

посмотреть на осциллографе
Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот 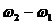 - частотой биений (циклической).
- частотой биений (циклической).
При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).
например, сложим два колебания с одинаковыми частотами:
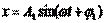
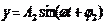
исключив время, получим:
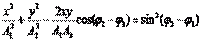
В общем случае это - уравнение эллипса. При A1=A2 - окружность, при 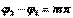 (m - целое) - отрезок прямой.
(m - целое) - отрезок прямой.
Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.
30. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу. (выше уже было об этом, но все же…)
Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде
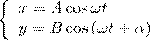 (1)
(1)
где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как
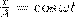
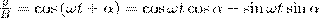
и заменяя во втором уравнении 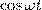 на
на 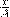 и
и 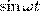 на
на  , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
, найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
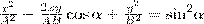 (2)
(2)
Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес:
1) α = mπ (m=0, ±1, ±2, ...). В этом случае эллипс становится отрезком прямой
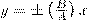 (3)
(3)
где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой , которое совершается вдоль прямой (3), составляющей с осью х угол . В этом случае имеем дело с линейно поляризованными колебаниями;
2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае уравнение станет иметь вид
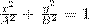 (4)
(4)
Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями иликолебаниями, поляризованными по кругу.
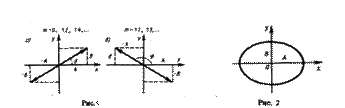
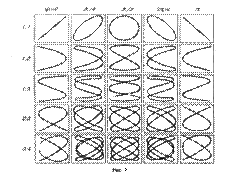
Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ).
Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.
Волны
Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, увлекаемые частицы будут отставать по фазе от тех частиц, которые их увлекают.
При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды. Среда рассматривается как сплошная, т.е. непрерывно распределенная в пространстве и обладающая упругими свойствами.
Итак, колеблющееся тело, помещенное в упругую среду, является источником колебаний, распространяющихся от него во все стороны. Процесс распространения колебаний в среде называется волной.
При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице передается лишь состояние колебательного движения и энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Волны бывают поперечными (колебания происходят в плоскости, перпендикулярной направлению распространения) и продольными (сгущение и разрежение частиц среды происходит в направлении распространения).
Граница, отделяющая колеблющиеся частицы от частиц еще не начавших колебаться, называется фронтом волны.
В однородной среде направление распространения перпендикулярно фронту волны
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l:
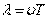 |
где υ – скорость распространения волны, – период, ν – частота. Отсюда скорость распространения волны можно найти по формуле:
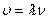 |
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченную волновым процессом, т.е. волновых поверхностей бесконечное множество. Волновые поверхности остаются неподвижными (они проходят через положение равновесия частиц, колеблющихся в одинаковой фазе). Волновой фронт только один, и он все время перемещается.
Волновые поверхности могут быть любой формы. В простейших случаях волновые поверхности имеют форму плоскости или сферы, соответственно волны называются плоскими илисферическими. В плоской волне волновые поверхности представляют собой систему параллельных друг другу плоскостей, в сферической волне – систему концентрических сфер.
Уравнение бегущей волны
Уравнение плоской одномерной синусоидальной волны:
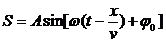
(Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. v - скорость распространения волны, А - амплитуда волны, аргумент синуса - фаза волны, - начальная фаза колебаний в точке х = 0, - частота (циклическая) волны.
Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ = .
ВОЛНОВОЕ ЧИСЛО k:
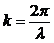
С помощью введенного волнового числа уравнение волны запишется:
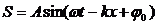
Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести ВОЛНОВОЙ ВЕКТОР k, модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:
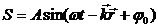
здесь r - радиус вектор точки пространства; - начальная фаза колебаний в начале координат.
Уравнение сферической волны отличается тем, что амплитуда волны убывает с расстоянием от источника:

= const по смыслу формулы есть амплитуда волны на единичном расстоянии от источника.
Уравнение волны в дифференциальной форме обычно называют волновым уравнением; вид этого уравнения следующий:
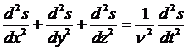 или
или 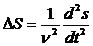
| Здесь S - оператор |
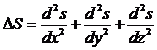
Уравнение синусоидальной волны является решением волнового уравнения (можно проверить подстановкой). Общее же решение волнового уравнения следующее:
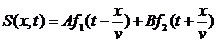
Здесь А и В - произвольные константы, а f1 и f2 - произвольные дважды дифференцируемые функции. Первое слагаемое описывает волну, распространяющуюся слева направо, второе - встречную волну.
В многомерном случае однородное волновое уравнение записывается в виде
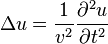 ,
,
где 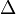 — оператор Лапласа,
— оператор Лапласа, 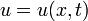 — неизвестная функция,
— неизвестная функция, 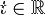 — время,
— время, 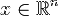 — пространственная переменная,
— пространственная переменная, 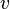 — фазовая скорость.
— фазовая скорость.
В одномерном случае уравнение называется также уравнением колебания струны или уравнением продольных колебаний стержня и записывается в виде
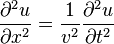 .
.
Неоднородное уравнение
Допустимо также рассматривать неоднородное волновое уравнение
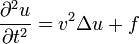 ,
,
где 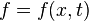 — некая заданная функция внешнего воздействия (внешней силы).
— некая заданная функция внешнего воздействия (внешней силы).
Стационарным вариантом волнового уравнения является уравнение Лапласа (уравнение Пуассона в неоднородном случае).
Задача нахождения нормальных колебаний системы, описываемой волновым уравнением, приводит к задаче на собственные значения для уравнения Лапласа, то есть к нахождению решений уравнения Гельмгольца, получающегося подстановкой
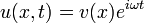 или
или 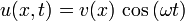 .
.
