Общее решение дифференциальных уравнений.

Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff, например, дифференциальное уравнение y''+y=x записывается в виде: diff(y(x),x$2)+y(x)=x.

Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2, и т.д.

Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была четко видна, структура этого решения. Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме общего решения соответствующего однородного дифференциального уравнения и частного решения этого же неоднородного дифференциального уравнения. Поэтому в строке вывода решение неоднородного линейного дифференциального уравнения всегда состоит из слагаемых, которые содержат произвольные постоянные (это общее решения соответствующего однородного дифференциального уравнения), и слагаемых без произвольных постоянных (это частное решения этого же неоднородного дифференциального уравнения).

Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командойrhs(%).

Задание 2.1.

1. Найти общее решение дифференциального уравнения y'+ycosx=sinxcosx.

> restart;

> de:=diff(y(x),x)+y(x)*cos(x)=sin(x)*cos(x);

de:=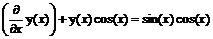

> dsolve(de,y(x));

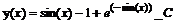1

Итак, решение искомого уравнения есть функция 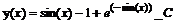1.

Замечание: при записи решения диффреренциального уравнения в Maple в строке вывода произвольная постоянная обозначена как _С1.

2. Найти общее решение дифференциального уравнения второго порядка y''-2y'+y=sinx+e^-x.

> restart;

>deq:=diff(y(x),x$2)-2*diff(y(x),x)+y(x)

=sin(x)+exp(-x);

deq:=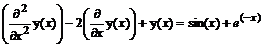

> dsolve(deq,y(x));

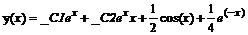
Замечание: так как исходное уравнение было второго порядка, то полученное решение содержит две произвольные константы, которые в Maple обычно обознаются как _С1 и _С2. Первые два слагаемых представляют собой общее решение соответствующего однородного дифференциального уравнения, а вторые два – частное решение неоднородного дифференциального уравнения.

3. Найти общее решение дифференциального уравнения порядка y''+k²y=sin(qx) в двух случаях: q¹k и q=k (резонанс).

> restart; de:=diff(y(x),x$2)+k^2*y(x)=sin(q*x);

dsolve(de,y(x));

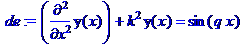
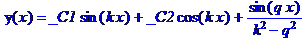
Теперь найдем решение в случае резонанса. Для этого перед вызовом команды dsolve следует приравнять q=k.

> q:=k: dsolve(de,y(x));

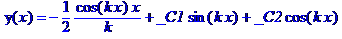
Замечание: в обоих случаях частное решение неоднородного уравнения и общее решение, содержащее произвольные постоянные, выводятся отдельными слагаемыми.