Оценивание вещественных выражений.

В Maple имеются следующие команды оценивания вещественных выражений:

frac(expr) – вычисление дробной части выражения expr;

trunc(expr) – вычисление целой части выражения expr;

round(expr) – округление выражения expr;

Оценивание комплексных выражений.

Вещественную и мнимую части комплексного выражения z=x+iy можно найти с помощью команд Re(z)и Im(z). Например:

> z:=3+I*2:

> Re(z);Im(z);

3, 2

Если z=x+iy, то комплексно сопряженное ему выражение w=z*=x–iy можно найти с помощью команды conjugate(z). Продолжение предыдущего примера:

w:=conjugate(z);

w:=3–2 I

Модуль и аргумент комплексного выражения z можно найти с помощью команды polar(z), которую необходимо предварительно вызвать из стандартной библиотеки командой readlib. Например:

> readlib(polar): polar(I);

polar

В строке вывода в скобках через запятую указаны модуль числа i, равный единице и его аргумент, равный .

Если комплексное выражение очень сложное или содержит параметры, то команды Re(z)и Im(z)не дают требуемого результата. Получить вещественную и мнимую части комплексного выраженияz можно, если использовать команду преобразования комплексных выражений evalc(z). Например:

> z:=ln(1-I*sqrt(3))^2;

> evalc(Re(z)); evalc(Im(z));

Задание 2.

1. Дано число а=57/13. Найти его целую часть x и дробную часть y и убедиться, что a=x+y. Наберите:

> a:=57/13:

> y:=frac(a);

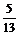
> x:=trunc(a);

> x+y;

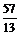
2. Дано комплексное число 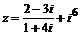. Найти его вещественную и мнимую части, а затем комплексно сопряженное ему число w и убедиться, что w+z=2Re(z).

В командной строке наберите:

> z:=(2-3*I)/(1+4*I)+I^6:

> Re(z); Im(z);

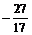
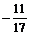
> w:=conjugate(z);

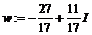
> z+w;

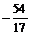
3.Найти модуль и аргумент комплексного числа 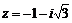и вычислить z⁴. Наберите:

> z:=-1-I*sqrt(3):

> readlib(polar): polar(z);

polar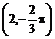

Чему равен модуль и аргумент этого числа?

> evalc(z^4);

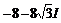
§3. Решение уравнений

Решение обыкновенных уравнений.

Для решения уравнений в Maple существует универсальная команда solve(eq,x), где eq – уравнение, x – переменная, относительно которой уравнение надо разрешить. В результате выполнения этой команды в строке вывода появится выражение, которое является решением данного уравнения. Например:

> solve(a*x+b=c,x);

Если уравнение имеет несколько решений, которые вам понадобятся для дальнейших расчетов, то команде solve следует присвоить какое-нибудь имя name. Обращение к какому-либо k–ому решению данного уравнения производится указанием его имени с номером решения k в квадратных скобках: name[k]. Например:

> x:=solve(x^2-a=0,x);

> x[1];

> x[2];

> x[1]+x[2];

Решение систем уравнений.

Системы уравнений решаются с помощью такой же команды solve({eq1,eq2,…},{x1,x2,…}), только теперь в параметрах команды следует указывать в первых фигурных скобках через запятую уравнения, а во вторых фигурных скобках перечисляются через запятую переменные, относительно которых требуется решить систему. Если вам будет необходимо для дальнейших вычислений использовать полученные решения уравнений, то команде solve следует присвоить какое-нибудь имя name. Затем выполняется присвоения команда assign(name). После этого над решениями можно будет производить математические операции. Например:

> s:=solve({a*x-y=1,5*x+a*y=1},{x,y});

s:={}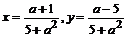

> assign(s); simplify(x-y);