Решение уравнений и неравенств

Решение уравнений и неравенств

1. Способы задания функций.Замена переменных.

2. Операции оценивания.

3. Решение уравнений.

4. Решение неравенств.

§1. Способы задания функций. Замена переменных

В Maple имеется несколько способов представления функции.

Способ 1. Определение функции с помощью оператора присваивания (:=): какому-то выражению присваивается имя, например:

> f:=sin(x)+cos(x);

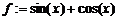
Если задать конкретное значение переменной х, то получится значение функции f для этого х. Например, если продолжить предыдущий пример и вычислить значение f при 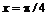, то следует записать:

> x:=Pi/4;

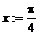
> f;

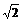
После выполнения этих команд переменная х имеет заданное значение .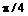

Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs({x1=a1, x2=a2,…, },f),где в фигурных скобках указываются переменные хi и их новые значения аi(i=1,2,…), которые следует подставить в функцию f. Например:

> f:=x*exp(-t);

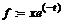
> subs({x=2,t=1},f);

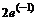
Все вычисления в Maple по умолчанию производятся символьно, то есть результат будет содержать в явном виде иррациональные константы, такие как, 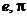и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf(expr,t),где expr – выражение,t – точность, выраженная в числах после запятой. Например, в продолжение предыдущего примера, вычислим полученное значение функции приближенно:

> evalf(%);

.7357588824

Здесь использован символ (%) для вызова предыдущей команды.

Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…). Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом:

> f:=(x,y)->sin(x+y);

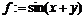
Обращение к этой функции осуществляется наиболее привычным в математике способом, когда в скобках вместо аргументов функции указываются конкретные значения переменных. В продолжение предыдущего примера вычисляется значение функции:

> f(Pi/2,0);

Способ 3. С помощью команды unapply(expr,x1,x2,…), где expr – выражение, x1,x2,… – набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например:

> f:=unapply(x^2+y^2,x,y);

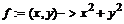
Ø f(-7,5);

В Maple имеется возможность определения неэлементарных функций вида

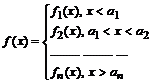
посредством команды

> piecewise(cond_1,f1, cond_2, f2, …).

Например, функция

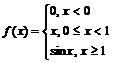
записывается следующим образом:

> f:=piecewise(x<0, 0, 0<=x and x<1, x, x>=1, sin(x));

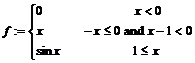
Задание 1.

Не забудьте, что выполнение всех последующих заданий должно начинаться с текстовой строки, содержащей «Задание №», где № – номер задания. Также помните, что для правильности вычислений перед выполнением каждого пункта задания следует выполнять команду restart. Перед выполнением контрольных заданий следует набирать в текстовом режиме «Контрольные задания». Эти правила оформления относятся ко всем лабораторным работам.

1. Запустите Maple. Переведите первую строку в текстовую и наберите в ней: «Лабораторная работа №2». Нажмите Enter. Строкой ниже наберите: «Выполнил студент ...» и свою фамилию, а на следующей строке наберите: «Задание №1».

2. Определите функцию 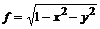и перейдите в ней к полярным координатам 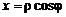, 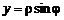. Упростите полученное выражение. Для этого наберите:

> f:=sqrt(1-x^2-y^2);

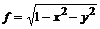
> f:=subs({x=rho*cos(phi),y=rho*sin(phi)},f);

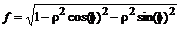
> f:=simplify(%);

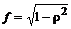
3. Определите функцию 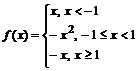и прибавьте к ней х. Для этого наберите:

> f:=piecewise(x<-1, x, -1<=x and x<1, -x^2, x>=1, -x);

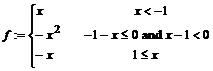
> %+x: simplify(%);

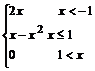
§2. Операции оценивания

Задание 2.

1. Дано число а=57/13. Найти его целую часть x и дробную часть y и убедиться, что a=x+y. Наберите:

> a:=57/13:

> y:=frac(a);

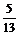
> x:=trunc(a);

> x+y;

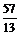
2. Дано комплексное число 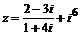. Найти его вещественную и мнимую части, а затем комплексно сопряженное ему число w и убедиться, что w+z=2Re(z).

В командной строке наберите:

> z:=(2-3*I)/(1+4*I)+I^6:

> Re(z); Im(z);

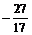
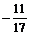
> w:=conjugate(z);

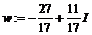
> z+w;

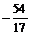
3.Найти модуль и аргумент комплексного числа 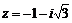и вычислить z⁴. Наберите:

> z:=-1-I*sqrt(3):

> readlib(polar): polar(z);

polar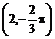

Чему равен модуль и аргумент этого числа?

> evalc(z^4);

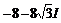
§3. Решение уравнений

Решение систем уравнений.

Системы уравнений решаются с помощью такой же команды solve({eq1,eq2,…},{x1,x2,…}), только теперь в параметрах команды следует указывать в первых фигурных скобках через запятую уравнения, а во вторых фигурных скобках перечисляются через запятую переменные, относительно которых требуется решить систему. Если вам будет необходимо для дальнейших вычислений использовать полученные решения уравнений, то команде solve следует присвоить какое-нибудь имя name. Затем выполняется присвоения команда assign(name). После этого над решениями можно будет производить математические операции. Например:

> s:=solve({a*x-y=1,5*x+a*y=1},{x,y});

s:={}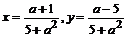

> assign(s); simplify(x-y);

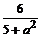
Задание 3.

1. Найти все решения системы уравнений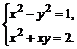

Наберите:

> eq:={x^2-y^2=1,x^2+x*y=2};

> _EnvExplicit:=true:

> s:=solve(eq,{x,y});

,

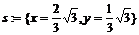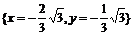
Теперь найдите сумму двух наборов решений. Наберите:

> x1:=subs(s[1],x): y1:=subs(s[1],y):

x2:=subs(s[2],x): y2:=subs(s[2],y):

> x1+x2; y1+y2;

Чему равны эти суммы решений?

2. Численно решите уравнение 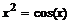. Наберите:

> x=fsolve(x^2=cos(x),x);

x=.8241323123

3. Найдите функцию f(x), удовлетворяющую уравнению 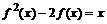. Наберите:

> F:=solve(f(x)^2-2*f(x)=x,f);

F:= proc(x) RootOf(_Z^2-2*_Z-x) end

> f:=convert(F(x), radical);

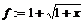
4. Найдите все решения уравнения 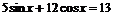. Наберите:

> _EnvAllSolutions:=true:

> solve(5*sin(x)+12*cos(x)=13,x);

~

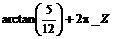§4. Решение неравенств

Решение простых неравенств.

Команда solve применяется также для решения неравенств. Решение неравенства выдается в виде интервала изменения искомой переменной. В том случае, если решение неравенства полуось, то в поле вывода появляется конструкция вида RealRange(–¥, Open(a)), которая означает, что xÎ(–¥, a), а – некоторое число. Слово Open означает, что интервал с открытой границей. Если этого слова нет, то соответствующая граница интервала включена во множество решений. Например:

> s:=solve(sqrt(x+3)<sqrt(x-1)+sqrt(x-2),x):

> convert(s,radical);

RealRange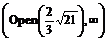

Если вы хотите получить решение неравенства не в виде интервального множества типа xÎ(a, b), а в виде ограничений для искомой переменной типа a<x, x< b, то переменную, относительно которой следует разрешить неравенство, следует указывать в фигурных скобках. Например:

> solve(1-1/2*ln(x)>2,{x});

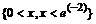
Решение систем неравенств.

С помощью команды solve можно также решить систему неравенств. Например:

> solve({x+y>=2,x-2*y<=1,x-y>=0,x-2*y>=1},{x,y});

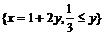
Задание 4.

1. Решите неравенство 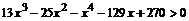. Наберите:

> solve(13*x^3-25*x^2-x^4-129*x+270>0,x);

RealRange(Open(-3), Open(2)), RealRange(Open(5), Open(9))

Запишите этот результат в аналитическом виде. Получите решение этого неравенства в виде ограничений для искомой переменной. Проделайте это самостоятельно.

2. Решите неравенство 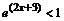. Наберите:

> solve(exp(2*x+3)<1,x);

RealRange

Теперь получите самостоятельно решение этого неравенства в виде ограничений для искомой переменной.

3. Выполните все контрольные задания. Перед их выполнением наберите в текстовом режиме «Контрольные задания». Результаты выполнения заданий покажите преподавателю. Сохраните файл со всеми выполненными заданиями на диск. Ответьте на все контрольные вопросы.

Контрольные задания.

При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:

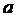- число букв в фамилии студента,

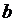- число букв в полном имени студента,

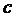- число букв в отчестве студента.

В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, отчество, фамилия).

Задания.

1. Дано комплексное число 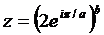. Найти его вещественную и мнимые части, модуль и аргумент.

2. Записать функцию 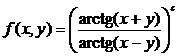в виде функционального оператора и вычислите ее значения при x=1, y=0 и при , .

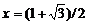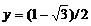3. Записать функцию 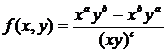с помощью оператора присваивания и вычислите ее значение при x=d, y=1/d, используя команду подстановки subs.

4. Найти все точные решения системы 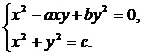в аналитическом виде.

5. Найти все решения тригонометрического уравнения .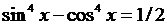

6. Найти численное решение уравнения .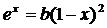

7. Решить неравенство .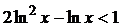

Контрольные вопросы.

1. Опишите способы задания функций в Maple.

2. Какие операции оценивания производятся в Maple с действительными выражениями?

3. Для чего предназначена команда evalf?

4. С помощью каких команд можно найти вещественную и мнимую части комплексного выражения, а также его модуль и аргумент, и комплексно сопряженное ему число? Какую роль выполняет команда evalc?

5. Для чего предназначена команда solve?

6. Какие команды используются для численного решения уравнений и для решения рекуррентных уравнений?

7. Какие дополнительные команды следует ввести для того, чтобы получить точное решение уравнения, все решения уравнения?

8. В каком виде выдается решение неравенства? Как отличить в строке вывода закрытый интервал от открытого?

Решение уравнений и неравенств

1. Способы задания функций.Замена переменных.

2. Операции оценивания.

3. Решение уравнений.

4. Решение неравенств.

§1. Способы задания функций. Замена переменных

В Maple имеется несколько способов представления функции.

Способ 1. Определение функции с помощью оператора присваивания (:=): какому-то выражению присваивается имя, например:

> f:=sin(x)+cos(x);

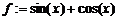
Если задать конкретное значение переменной х, то получится значение функции f для этого х. Например, если продолжить предыдущий пример и вычислить значение f при 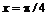, то следует записать:

> x:=Pi/4;

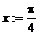
> f;

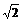
После выполнения этих команд переменная х имеет заданное значение .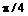

Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs({x1=a1, x2=a2,…, },f),где в фигурных скобках указываются переменные хi и их новые значения аi(i=1,2,…), которые следует подставить в функцию f. Например:

> f:=x*exp(-t);

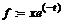
> subs({x=2,t=1},f);

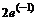
Все вычисления в Maple по умолчанию производятся символьно, то есть результат будет содержать в явном виде иррациональные константы, такие как, 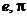и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf(expr,t),где expr – выражение,t – точность, выраженная в числах после запятой. Например, в продолжение предыдущего примера, вычислим полученное значение функции приближенно:

> evalf(%);

.7357588824

Здесь использован символ (%) для вызова предыдущей команды.

Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…). Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом:

> f:=(x,y)->sin(x+y);

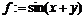
Обращение к этой функции осуществляется наиболее привычным в математике способом, когда в скобках вместо аргументов функции указываются конкретные значения переменных. В продолжение предыдущего примера вычисляется значение функции:

> f(Pi/2,0);

Способ 3. С помощью команды unapply(expr,x1,x2,…), где expr – выражение, x1,x2,… – набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например:

> f:=unapply(x^2+y^2,x,y);

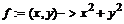
Ø f(-7,5);

В Maple имеется возможность определения неэлементарных функций вида

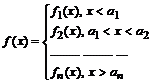
посредством команды

> piecewise(cond_1,f1, cond_2, f2, …).

Например, функция

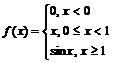
записывается следующим образом:

> f:=piecewise(x<0, 0, 0<=x and x<1, x, x>=1, sin(x));

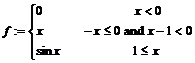
Задание 1.

Не забудьте, что выполнение всех последующих заданий должно начинаться с текстовой строки, содержащей «Задание №», где № – номер задания. Также помните, что для правильности вычислений перед выполнением каждого пункта задания следует выполнять команду restart. Перед выполнением контрольных заданий следует набирать в текстовом режиме «Контрольные задания». Эти правила оформления относятся ко всем лабораторным работам.

1. Запустите Maple. Переведите первую строку в текстовую и наберите в ней: «Лабораторная работа №2». Нажмите Enter. Строкой ниже наберите: «Выполнил студент ...» и свою фамилию, а на следующей строке наберите: «Задание №1».

2. Определите функцию 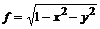и перейдите в ней к полярным координатам 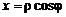, 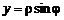. Упростите полученное выражение. Для этого наберите:

> f:=sqrt(1-x^2-y^2);

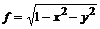
> f:=subs({x=rho*cos(phi),y=rho*sin(phi)},f);

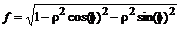
> f:=simplify(%);

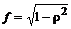
3. Определите функцию 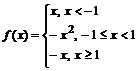и прибавьте к ней х. Для этого наберите:

> f:=piecewise(x<-1, x, -1<=x and x<1, -x^2, x>=1, -x);

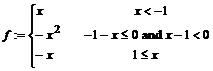
> %+x: simplify(%);

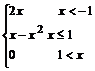
§2. Операции оценивания