Вычисление коэффициента корреляции.

Лабораторная работа № 3

Статистические связи

Задание по работе

1. Законспектировать основные положения раздела 2.

Используя данные таблицы 1( 3-х месяцев), определить:

· Коэффициенты парной корреляции.

· уравнение линейной регрессии,

· уравнение нелиней регрессии,

· уравнение множественной регрессии

2. Записать полученные значения и уравнения в тетрадь, провести расчет значений параметров (температур ) по полученным уравнениям, вычислить средние значения отклонений расчетных значений от исходных, т.е. среднюю погрешность.

3. Записать выводы о возможности использования полученных уравнений для прогноза температур будущих периодов.

2.Основные понятия

Балансовая связь — характеризует зависимость между источниками формирования ресурсов (средств) и их использованием.

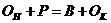
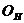— остаток товаров на начало отчетного периода;

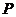— поступление товаров за период;

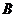— выбытие товаров в изучаемом периоде;

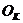— остаток товаров на конец отчетного периода.

Левая часть формулы характеризует предложение товаров

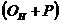, а правая часть — использование товарных ресурсов .

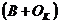Компонентные связи показателей коммерческой деятельности характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители:

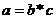
Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. При этом одни показатели выступают как факторные, а другие — как результативные.

Факторные связи могут рассматриваться как функциональные и корреляционные.

При функциональной связи изменение результативного признака 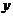всецело зависит от изменения факторного признака :

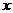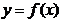
При корреляционной связи изменение результативного признака 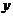не всецело зависит от факторного признака 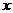, а лишь частично, так как возможно влияние прочих факторов :

.

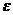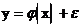Для того, чтобы установить, есть ли зависимость между величинами, используются многообразные статистические методы, позволяющие определить, во-первых — какие связи; во-вторых — тесноту связи (в одном случае она сильная, устойчивая, в другом — слабая); в-третьих — форму связи (т.е. формулу, связывающую величину 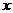и ).

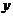Для определения тесноты корреляционной связи применяется коэффициент корреляции.

Коэффициент корреляции изменяется от -1 до +1 и показывает тесноту и направление корреляционной связи.

Если отклонения 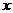по и по 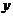от среднего совпадают и по знаку, и по величине, то это полная прямая связь, то 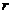=+1.

Если полная обратная связь, то 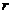=-1.

Если связь отсутствует, то 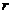=0.

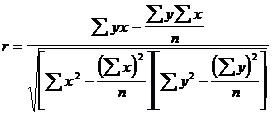
Построение уравнений регрессии

Линейная регрессия

В регрессионном анализе изучается связь и определяется количественная зависимость между зависимой переменной и одной или несколькими независимыми переменными. Пусть переменная Yзависит от одной переменной X. При этом предполагается, что переменная X принимает заданные фиксированные значения, а зависимая переменная Yимеет случайный разброс из-за ошибок измерения, влияния неучтенных факторов и т.д. Каждому значению X соответствует некоторый закон распределения вероятностей случайной величины Y. Предположим, что Yв «среднем» линейно зависит от значений переменной X. Это означает, что условное математическое ожидание случайной величины Y при заданном значении X имеет вид

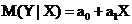. (1)

Данная функция называется линейной теоретической функцией регрессии Y на X, а параметры a₀ и a₁ – параметрами линейной регрессии (коэффициенты регрессии). На практике параметры регрессии определяются по результатам наблюдений переменных Y и X, связь, между которыми, можно записать в виде

,

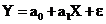где e - случайная ошибка наблюдений. В регрессионном анализе полагают, что случайные ошибки наблюдений имеют нормальный закон распределения, то есть

.

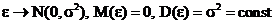Также считают, что отсутствует автокорреляция между ошибками, т.е. последовательные значения ошибок в каждом опыте e_i не зависят друг от друга

Точность аппроксимации с помощью прямой (y = m^x + b), вычисленной по функции ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель (уравнение), полученная по функции. Функция ЛИНЕЙН использует метод наименьших квад­ратов для определения наилучшей аппроксимации данных. Когда имеется только одна неза­висимая переменная x, то m и b вычисляются по следующим формулам: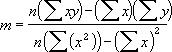

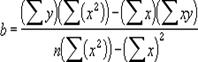
Формат функции: ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика)

Конст - это логическое значение, которое указывает, требуется ли, чтобы кон­станта b была равна 0. Если конст. имеет значение ИСТИНА или опущено, то b вычисляется обыч­ным образом. Если конст имеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y = mx.

Статистика - это логическое значение, которое указывает, требуется ли рассчитать дополнительную статистику по регрессии. Если статистика имеет значение ИСТИНА, то функция ЛИНЕЙН расчитывает дополнительную регрессионную статистику, так что возвращаемый массив бу­дет иметь вид: {mn;mn-1;...;m1;b:sen; sen- b*...; se1; seb:r2;sey:F; df:ssreg;ssresid}. Если статистика имеет значение ЛОЖЬ или опущена, то функция ЛИНЕЙН расчитывает только коэффициенты m и постоянную b.

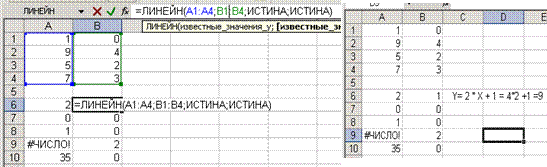На рис1. показано определение уравнения регрессии по двум переменным Xi и Yi.

Рис.1

Для расчета и вывода значений m и bзависимостей выделяются 2 ячейки, вызывают функцию, вводят исходные данные X и Y, указывают КОНСТ- истинаи СТАТИС – истина, нажимают Ctrl + Shift +Enter, и с полученными коэффициентами m и b записывают уравнение.

На рисунке 2 показан расчет линейной регрессии при задании одной (определяемой) пере­менной Yi. Независимые переменные Хi при этом берутся в виде натурального ряда чисел.

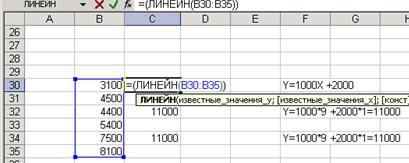
Рис. 2.

Лабораторная работа № 3

Статистические связи

Задание по работе

1. Законспектировать основные положения раздела 2.

Используя данные таблицы 1( 3-х месяцев), определить:

· Коэффициенты парной корреляции.

· уравнение линейной регрессии,

· уравнение нелиней регрессии,

· уравнение множественной регрессии

2. Записать полученные значения и уравнения в тетрадь, провести расчет значений параметров (температур ) по полученным уравнениям, вычислить средние значения отклонений расчетных значений от исходных, т.е. среднюю погрешность.

3. Записать выводы о возможности использования полученных уравнений для прогноза температур будущих периодов.

2.Основные понятия

Балансовая связь — характеризует зависимость между источниками формирования ресурсов (средств) и их использованием.

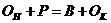
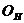— остаток товаров на начало отчетного периода;

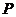— поступление товаров за период;

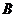— выбытие товаров в изучаемом периоде;

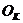— остаток товаров на конец отчетного периода.

Левая часть формулы характеризует предложение товаров

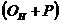, а правая часть — использование товарных ресурсов .

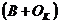Компонентные связи показателей коммерческой деятельности характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители:

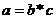
Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. При этом одни показатели выступают как факторные, а другие — как результативные.

Факторные связи могут рассматриваться как функциональные и корреляционные.

При функциональной связи изменение результативного признака 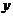всецело зависит от изменения факторного признака :

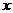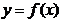
При корреляционной связи изменение результативного признака 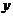не всецело зависит от факторного признака 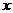, а лишь частично, так как возможно влияние прочих факторов :

.

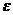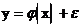Для того, чтобы установить, есть ли зависимость между величинами, используются многообразные статистические методы, позволяющие определить, во-первых — какие связи; во-вторых — тесноту связи (в одном случае она сильная, устойчивая, в другом — слабая); в-третьих — форму связи (т.е. формулу, связывающую величину 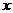и ).

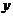Для определения тесноты корреляционной связи применяется коэффициент корреляции.

Коэффициент корреляции изменяется от -1 до +1 и показывает тесноту и направление корреляционной связи.

Если отклонения 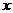по и по 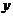от среднего совпадают и по знаку, и по величине, то это полная прямая связь, то 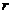=+1.

Если полная обратная связь, то 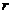=-1.

Если связь отсутствует, то 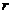=0.

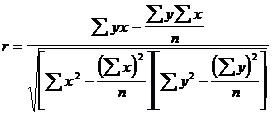
Вычисление коэффициента корреляции.

Важной характеристикой наличия взаимосвязи между параметрами является ко­эффициент корреляции. Для вычисления его значения необходимо ввести 2 массива дан­ных (ячейки Ai , Bi) по N => 20 значений. Этот коэффициент может принимать значения от 0 до 1. Чем выше значение коэффициента, тем больше взаимосвязь и тем больше она приближается к функциональной связи. Например, можно установить зависимость ме­жду средней температурой в помещении и использованием кондиционера. Коэффициент корреляциинаходится по стандартной функции:

КОРРЕЛ(массив1;массив2)

Если он превышает 0.65, то можно определять регрес­сионные зависимости по взятым данным. Если нет, то исходные данные надо изме­нить.