Алгоритм решения задачи численного интегрирования по формуле прямоугольников.

Задача. Вычислить интеграл I= 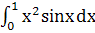, по формуле трапеций, разделив отрезок [0,1] на 10 равных частей, и оценить погрешность вычислений.

Решение проведем, используя формулы (18), (19) и принимая h=0,1:

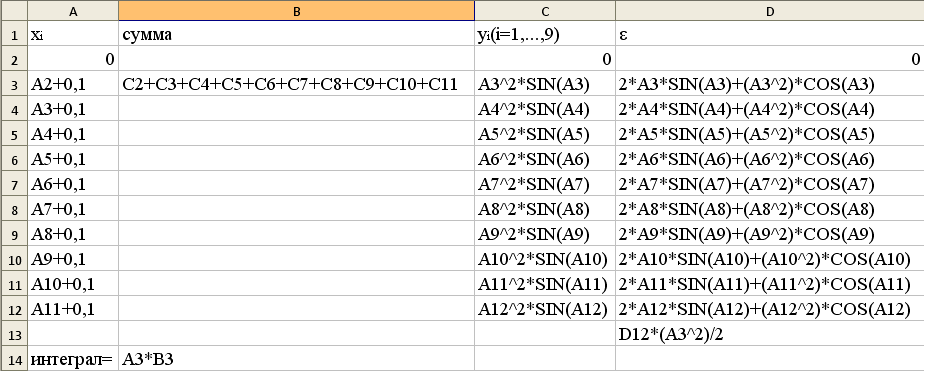
Результат:

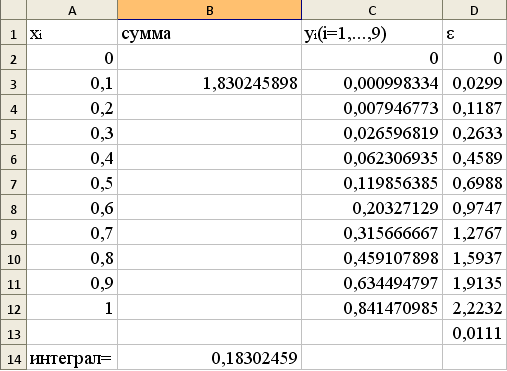
I=0,183±0,01.

Метод нерационален, т.к. обладает наименьшей точностью среди приведенных в данном пункте.

Алгоритм решения задачи численного интегрирования по формуле трапеций.

Задача. Вычислить интеграл I= 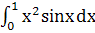, по формуле трапеций, разделив отрезок [0,1] на 10 равных частей, и оценить погрешность вычислений.

Решение. Воспользуемся формулами (14), (15) и примем h=0,1:

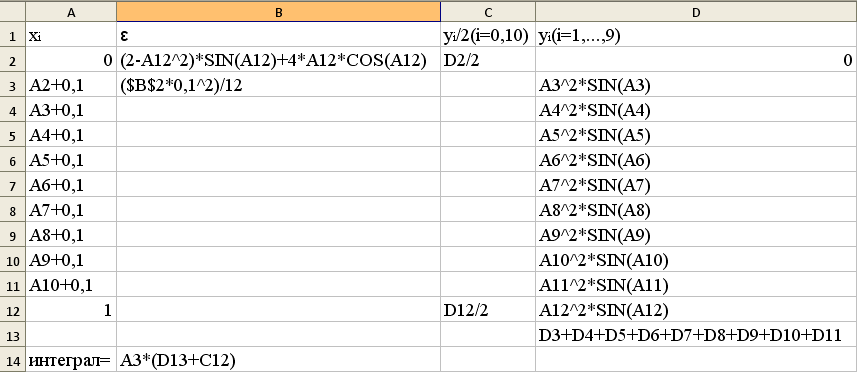
Результат:

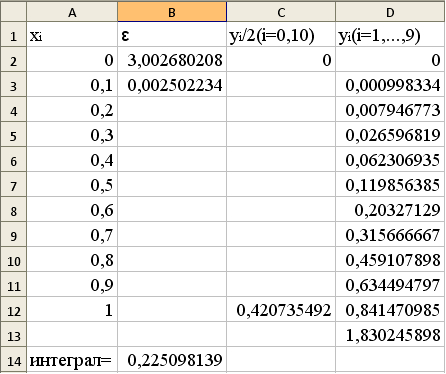
І = 0,225±0,003..

Алгоритм решения задачи численного интегрирования по формуле Симпсона (парабол).

Задача. Вычислить интеграл I= 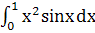, по формуле Симпсона, разделив отрезок [0,1] на 10 равных частей, и оценить погрешность вычислений.

Решение осуществим с помощью формул (16) и (17). Примем h=0,1:

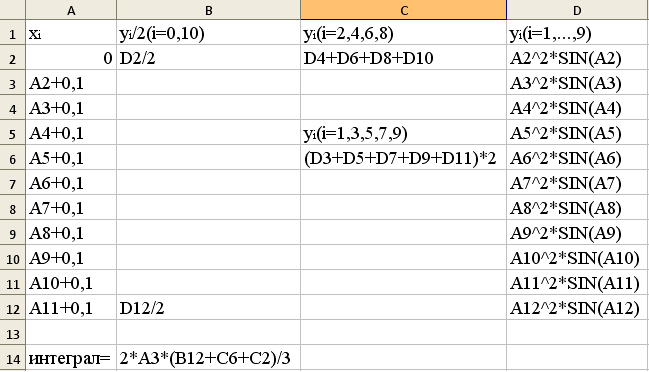
Результат:

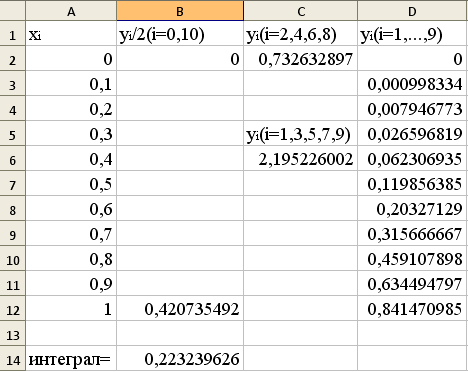
І =0,223±7,7·10^-6.

Метод Монте-Карло. Алгоритм решения в TMTPascal.

Задача. Вычислить определенный интеграл методом Монте-Карло

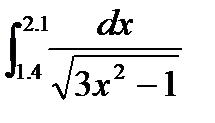
Решение:

program mk;

uses crt;

var x,s,integral,a,b,d: real;

i,n: integer;

function fun(x:real):real;

begin

fun:=1/sqrt(3*x*x-1);

end;

begin

randomize;

writeln('vvedite predely integrirovaniay');

read(a,b);

writeln('vvedite chislo sluchainyx ispytanii');

read(n);

s:=0;

d:=b-a;

for i:=1 to n do

begin

x:=a+d*((b-a)*random+a);

s:=s+fun(x);

end;

integral:=s*d/n;

writeln('i=',integral:17:11);

end.

Результат:

Задача.Методом Монте-Карло вычислить значение определенного интеграла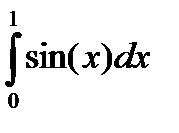

Решение

program MONTE_KARLO;

{y=sin x,a=0,b=1}

uses crt;

const n=10000;

var a,b,s,y,x:real;

i:integer;

BEGIN

clrscr;a:=0;b:=1;s:=0;

for i:=1 to n do

begin

x:=a+random*(b-a);

y:=sin(x);

s:=s+y;

end;

s:=(b-a)*s/n;

writeln('s=',s:10:5);

readln;

END.

Практическая часть

Задание 1.Вычислить интеграл 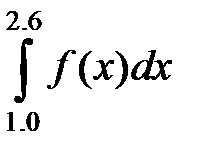, используя квадратурные формулы:

а) прямоугольников (левых, правых)с шагом 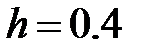; дать априорную оценку погрешности;

б) трапеций с шагам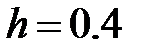и и 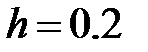; оценить погрешность результата по формуле Рунге и уточнить результат по Рунге;

в) Симпсона с шагом .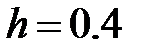

Промежуточные результаты вычислять с шестью значащими цифрами. Аргументы тригонометрических функций вычислять в радианах.

Образец решения:

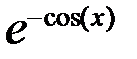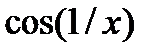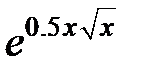а)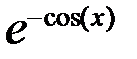

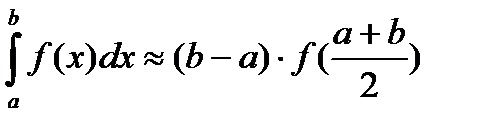
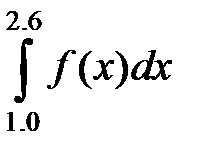
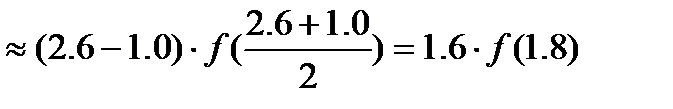
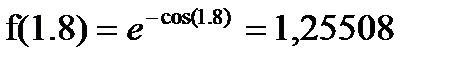
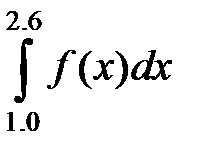
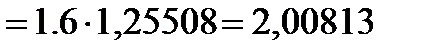
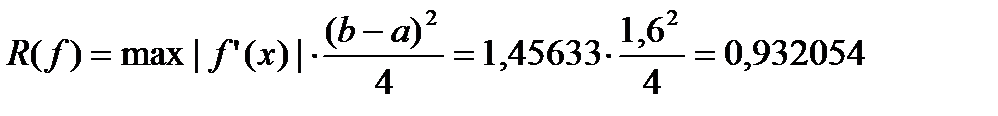
	x	y	y'
		0,582572	0,490218
	1,4	0,843693	0,831417
	1,8	1,255083	1,22226
	2,2	1,801286	1,456334
	2,6	2,35582	1,214428

а)метод прямоугольника

Метод прямоугольника
Прав	Лев
2,502352897	1,793054
2,147703371

I_прав=0,4*(∑ (y₁: y₄))= 2,50235

I_лев =0,4*(∑ (y₀: y₅))= 1,79305

I_общ =(I_прав+ I_лев)/2= 2,147703371

Оценим погрешность

|R_n|≤M₁*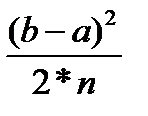

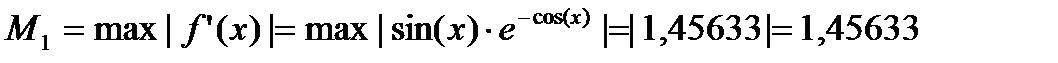
|R_n|≤1,456334*0,256=0,372822

б)

метод трапеций:

h=0.4

x	y
	0,540302
1,4	0,755561
1,8	0,849608
2,2	0,898461
2,6	0,926943

I_тр1=0,4*((y₀+ y₅)/2+∑( y_1: y₄))= 1,29490

.

h=0.2

x	y
	0,540302
1,2	0,672412
1,4	0,755561
1,6	0,810963
1,8	0,849608
	0,877583
2,2	0,898461
2,4	0,914443
2,6	0,926943

I_тр2=0,2*((y₀+ y₈)/2+∑( y_1: y₇))= 1,30253

оценим погрешность результата по формуле Рунге

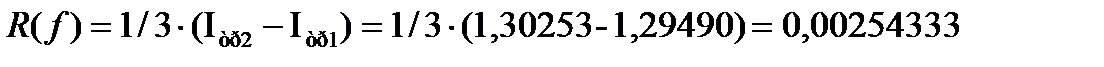
уточним результат по формуле Рунге

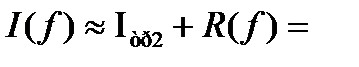1,30253+0,00254333=1,30507333

в)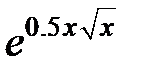

I_симп =0,4/3*( y₀+ y₄+4*( y₁+ y₃)+2*( y₂))= 6,14381.

№

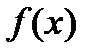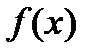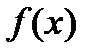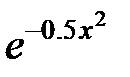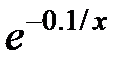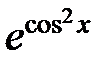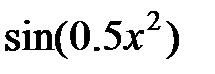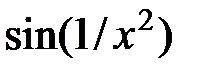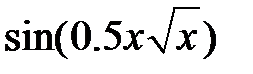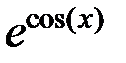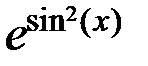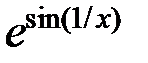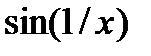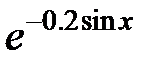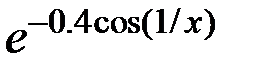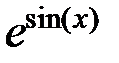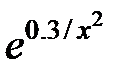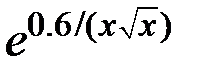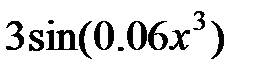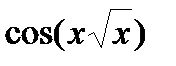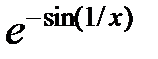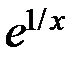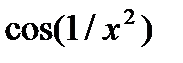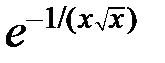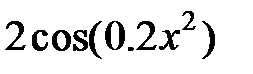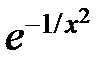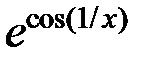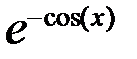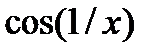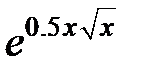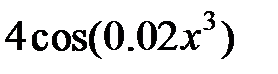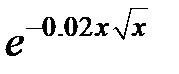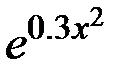Задание 2. Вычислить работу переменной силы F=F(x) по перемещению материальной точки М на линейном участке.

1<=x<=1,54, e=0.001

№ варианта	Вид функции
	F(x)

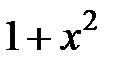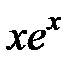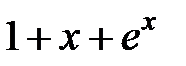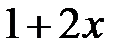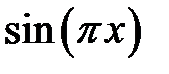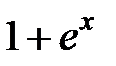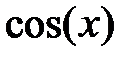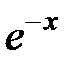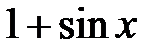Задание 3. Найти площадь фигуры, ограниченной линией у=f(x), на отрезке [0,1]

Вариант	f(x)

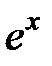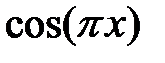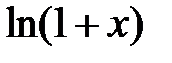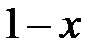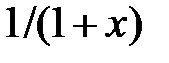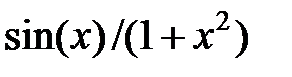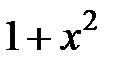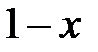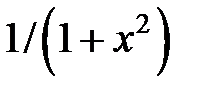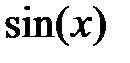Вопросы к защите лабораторной работы №5

«Численное интегрирование»

1. Простейшие квадратурные формулы (формулы правых, левых, центральных прямоугольников, формула трапеций, формула Симпсона), геометрическая иллюстрация, оценки погрешности. Точность квадратурных формул.

2. Квадратурные формулы интерполяционного типа: вывод формул, оценки погрешности.

3. Квадратурные формулы Гаусса: вывод формул, точность формул.

4. Метод Монте-Карло.

ЛАБОРАТОРНАЯ РАБОТА №6