Теория погрешностей и машинная арифметика

Теоретическая часть

Пусть х – некоторое число, число а называется его приближенным значением, если а в определенном смысле мало отличается от х и заменяет х в вычислениях, .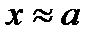

Погрешностью 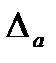приближенного значения а числа х называется разность 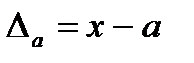, а модуль этой погрешностью называется абсолютной погрешностью.

Если 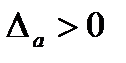, то а взято с недостатком. Если 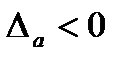, то а взято с избытком.

Границей погрешности приближенного значения а числа х называется всякое неотрицательное число 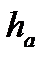, которое не меньше модуля погрешности: .

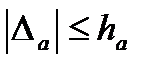Говорят, что приближение а приближает число х с точностью до 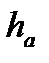, если , , .

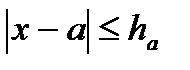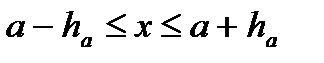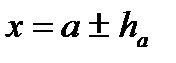Пример.Пусть а=0,273 – приближенное значение х с точность до 0,001. Указать границы, в которых заключается х.

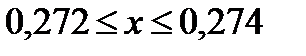
При округлении чисел считают, что границы погрешности округления равна половине единицы округляемого разряда:

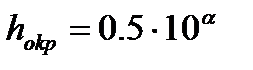, α – порядок округления разряда.

Относительной погрешностью приближенного значения а числа х называется отношение

.

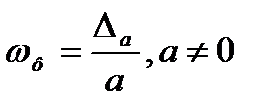Пример.Округлить до десятых число 27,52 и найти погрешность и относительную погрешность округления:

,

,

.

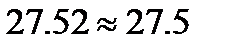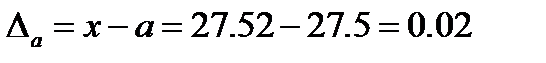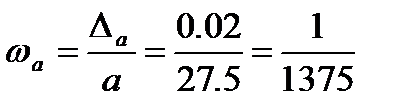Также как и абсолютная погрешность, относительная погрешность не всегда может быть вычислена и приходится оценивать ее модуль. Модуль относительной погрешности выражается в процентах. Чем меньше модуль относительной погрешности, тем выше качество приближения.

Пусть .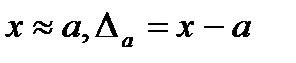

Цифра приближенного значения а называется верной, если модуль его погрешности не превосходит половины единицы этого разряда.

.

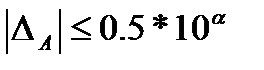Очевидно, что все цифры, стоящие слева от верной цифры – верные.

Пример. Пусть х=27,421, а=27,381, .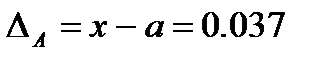

Выясним, какие цифры верные в приближении а?

4 – 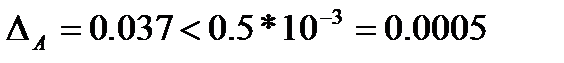, следовательно, 4 – неверная;

8 – 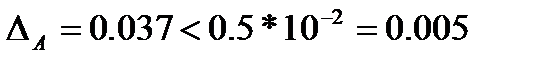, следовательно, 8 – неверная;

3 – 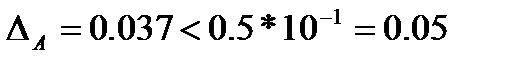, следовательно, 3 – верная.

3,2,7 – верные цифры.

Пример. Если известно, что относительная погрешность приближения 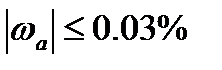, то это приближение имеет ровно 3 верные значащие цифры.

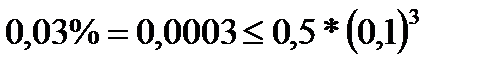, следовательно, приближение имеет не менее 3-х верных значащих цифр.

Практическая часть

Задание 1.Дана функция 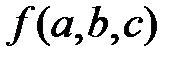. Значения переменных указаны в варианте со всеми верными цифрами. Оценить погрешность результата, используя: a) оценки погрешностей для арифметических операций; b) общую формулу погрешностей.

Результат представить в двух формах записи: с явным указанием погрешностей и с учетом верных цифр.

№					№
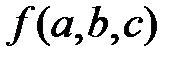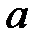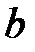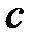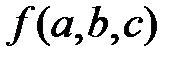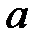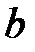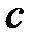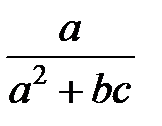		0.0125	0.283	0.0187		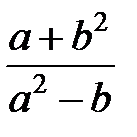	4.41	18.5
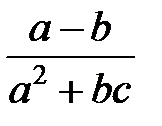		14.29	13.81	10.98		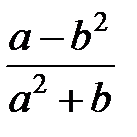	16.5	4.2
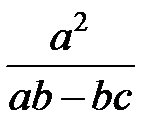		12.28	13.21	12.19		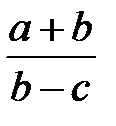	52.31	48.95	47.81
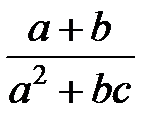		0.328	0.781	0.0129		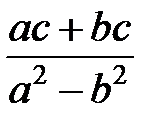	4.81	4.52	9.28
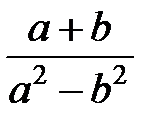		14.85	15.49		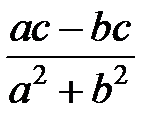		16.21	16.18	21.23
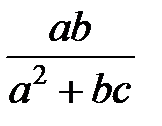		12.31	0.0352	10.82		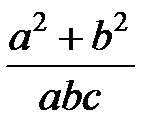		0.324	1.25
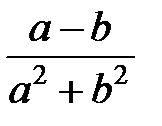		12.45	11.98		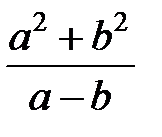		25.18	24.98
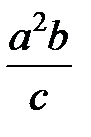		3.456	0.642	7.12		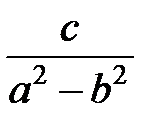	3.1415	3.1411	10.91
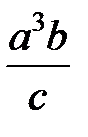		1.245	0.121	2.34		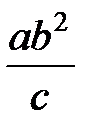	3.14	1.57	0.0921
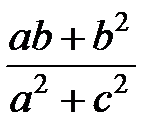		13.12	0.145	15.18		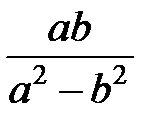	14.85	15.49
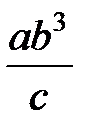		0.643	2.17	5.843		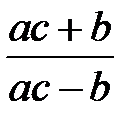	5.325	5.152	5.481
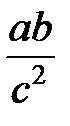		0.3575	2.63	0.854		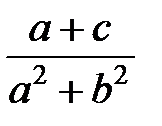	71.4	4.82	49.5
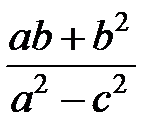		14.91	0.485	14.18		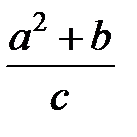	4.356	4.32	0.246
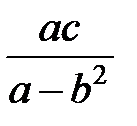		16.5	4.12	0.198		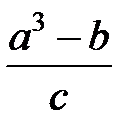	3.42	5.124	0.221
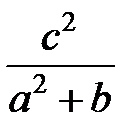		5.21	14.9	0.295		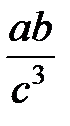	0.5761	3.622	0.0685

Задание 2.Вычислить значение и оценить абсолютную и относительную погрешности результата, считая, что значения исходных данных получены в результате округления.

Записать результат с учетом погрешности.

№		№

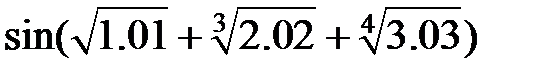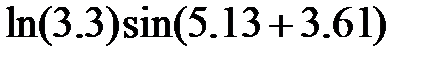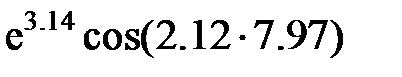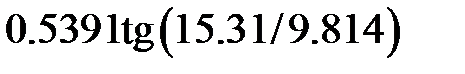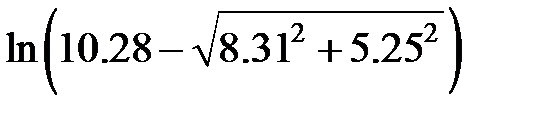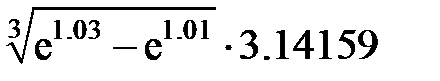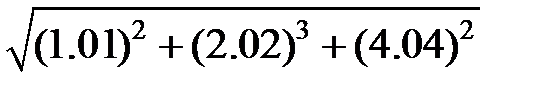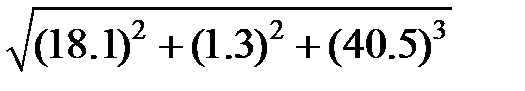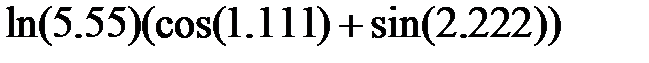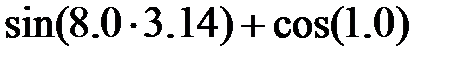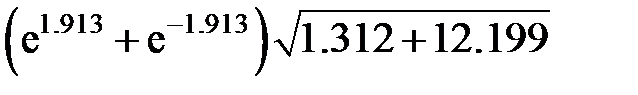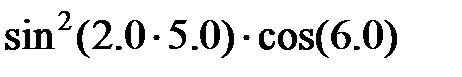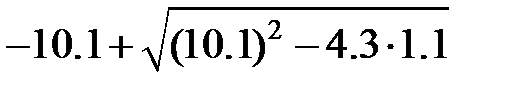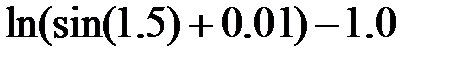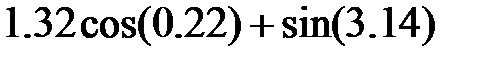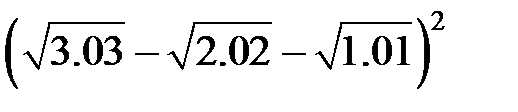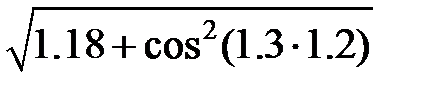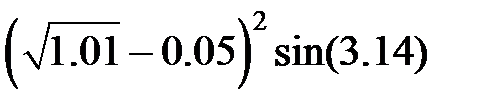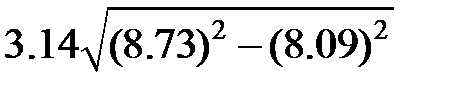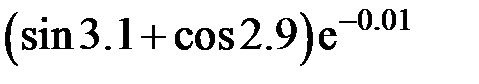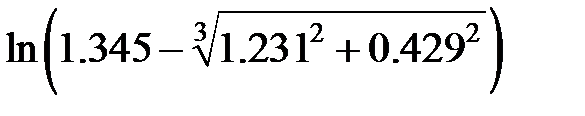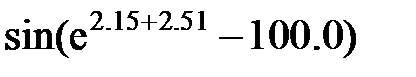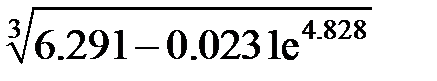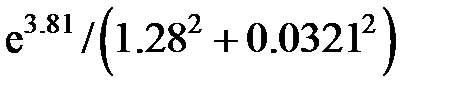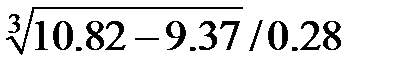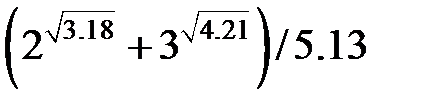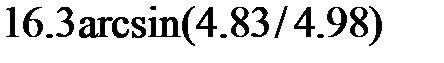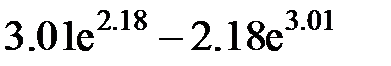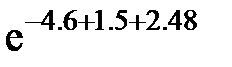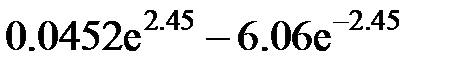Вопросы к защите лабораторной работы №1

«Теория погрешностей и машинная арифметика»

1. Источники и классификация погрешностей. Приближенные числа. Абсолютная и относительная погрешности. Верные и значащие цифры. Способы округления.

2. Погрешности арифметических операций над приближенными числами.

3. Погрешность вычисления функций одной и нескольких переменных.

ЛАБОРАТОРНАЯ РАБОТА № 2