Обработка результатов статистических исследований методами аппроксимации
В исходных данных задачи содержится таблица ряда измерений экспериментально полученной зависимости вида
| xi | x1 | x2 | x3 | . . . . | xn |
| yi | y1 | y2 | y3 | . . . . | yn |
Предполагается, что аналитическое выражение указанной зависимости неизвестно. Тогда возникает практически важная задача аппроксимации, которая заключается в том, чтобы найти такую простую аналитическую функцию y = j(x), значения которой в известных точкахxiпо возможности мало бы отличалось от опытных данных.
Аналитическая функция вида j(x), в пределах опыта с достаточной точностью определяющая зависимость между величинами x и y, называется эмпирической. К эмпирическим функциям могут относиться линейная y = a + bx, квадратичная y = a + bx + cx2и другие.
Введем величины Di = j(xi) – yi , которые назовем уклонениями. Это - расстояние по вертикальной оси от кривой j(x) до точек (xi, yi), взятые со знаком «+»или «–».
При решении задачи аппроксимации по методу наименьших квадратов полагают, что погрешность аппроксимации минимальна, если сумма квадратов уклонений d является наименьшей, т. е.
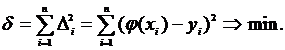 (7)
(7)
Аппроксимация эмпирической линейной функцией
Подставим в зависимость (7) выражение линейной функции. Получим
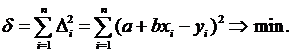
Величины а и внеизвестны. Их надо подобрать так, чтобы величина d приняла наименьшее значение. Известно, что в точке минимума частные производные функции обращаются в ноль, т. е. ¶d/¶a = 0 и ¶d/¶в = 0.
Найдя выражение для частных производных и приравняв их нулю, получим систему двух уравнений с двумя неизвестными а и в.После упрощения получим
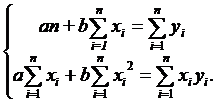
Решая эту систему уравнений методом Крамера, находим а и в.
Определитель системы:
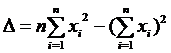
Определитель а:
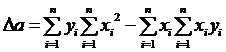 .
.
Определитель в:
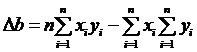 .
.
Неизвестные a = Da/D, b = Db/D.
Аппроксимация эмпирической квадратичной функцией
Подставим в зависимость (7) выражение квадратичной функции. Получим
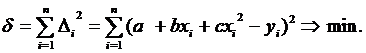
Величины а, ви снеизвестны. Найдя выражение для частных производных и приравняв их нулю, получим систему трех уравнений с тремя неизвестнымиа, вис.
После упрощения получим:
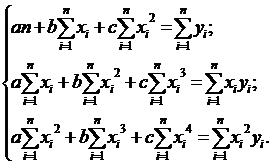
Решая эту систему уравнений методом Крамера, находима, ви с.
Определитель системы
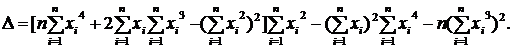
Определитель а
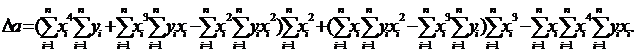
Определитель в
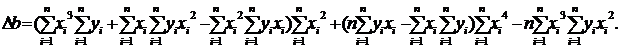
Определительс
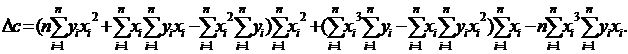
Неизвестные a = Da/D, b = Db/D, c = Dc/D.
Приложение 1

Министерство общего и профессионального образования
Российской Федерации
Санкт-Петербургская государственная лесотехническая академия
Сыктывкарский лесной институт
Факультет__________________________
Курс_______________________________
Группа_____________________________
Специальность______________________
КУРСОВАЯ РАБОТА ПО ИНФОРМАТИКЕ
Тема ______________________________
Студент ___________________________
Руководитель ______________________
СЫКТЫВКАР 1999
Приложение 2
Фрагменты программ, наиболее часто используемых студентами при выполнении курсового задания (для алгоритмического языка QBasic).
Окна и меню
DIM B$ (13)
B$ (0)=" "
B$(1)= " КУРСОВАЯ РАБОТА ПО ИНФОРМАТИКЕ "
B$ (2)=" Выполнил Иванов Иван Иванович "
B$ (3)=" студент 2-го курса, специальность ТХПД, д/о "
B$ (4)=" 1998 г. "
B$ (5)=" "
B$ (6)=" СТАТИСТИКА ХИМИЧЕСКИХ РЕАКТОРОВ "
B$ (7)=" МЕНЮ: "
B$ (8)=" 1. Формирование файла данных "
B$ (9)=" 2. Просмотр файла данных "
B$ (10)=" 3. Загрузка файла данных и решение задачи "
B$ (11)=" 4. Графическая иллюстрация результатов "
B$ (12)=" 5. Выход "
B$ (13)=" "
COLOR 15,2:CLS ‘ цвет (цвет символов с 0 по15, цвет фона с 0 по 7)
LOCATE 4 ‘ установить курсор в 4-ой строке экрана
FOR I=0 TO 5
PRINT TAB(18): COLOR 15,1: PRINT B$(I): COLOR 15,2
NEXT I
LOCATE 23,22 ‘ установить курсор в 23-ой строке и 22-ой позиции экрана
COLOR 15 : PRINT "Для продолжения нажмите любую клавишу"
SLEEP 100 ' выждать 100 сек или нажать любую клавишу
7 COLOR 15,2 : CLS : LOCATE 6
FOR I=5 TO 13
PRINT TAB(18) :COLOR 14,6: PRINT B$(I):COLOR 15,2
NEXT I
LOCATE 17,25: COLOR 15,5
INPUT " ВВЕДИТЕ НУЖНЫЙ НОМЕР"; NM:COLOR 15,2
6 ON NM GOTO 1,2,3,4,5
LOCATE 20,27: COLOR 14 : INPUT "Уточните номер"; NM : GOTO 6
1 ‘ Формирование файла данных
COLOR 7,0 : CLS
. . . .
GOTO 7
2 ‘ Просмотр файла данных
COLOR 7,0 : CLS
. . . .
LOCATE 23,18
COLOR 14 : PRINT "Для продолжения нажмите любую клавишу"
SLEEP 100 : GOTO 7
3 ‘ Загрузка файла данных и решение задачи
COLOR 7,0 : CLS
. . . .
LOCATE 23,18
COLOR 14 : PRINT "Для продолжения нажмите любую клавишу"
SLEEP 100 : GOTO 7
4 ‘ Графическая иллюстрация результатов
COLOR 7,0 : CLS
. . . .
LOCATE 23,18
COLOR 14 : PRINT "Для продолжения нажмите любую клавишу"
SLEEP 100 : GOTO 7
5 COLOR 7,0 : CLS
END
Вывод таблиц результатов
CLS
READ TN,TK,HT,A
DATA 0,20,2,3.2
Z$=" Равноускоренное движение точки "
L$="———————--———————————————————"
H$="| № п/п | t, сек | S, м | V, м/с |"
F$="| ## | ## | ###.# | ##.# |"
PRINT Z$
PRINT L$
PRINT H$
PRINT L$
N=1
FOR T=TN TO TK STEP HT
S=A*T^2/2
V=A*T
PRINT USING F$;N,T,S,V
N=N+1
NEXT T
PRINT L$
END
