Разложение сигнала на типовые составляющие

Исходя из временного представления сигнала (рисунок 1.1), разложим его на типовые составляющие, включающиеся в определенный момент времени. Для этого используем единичную функцию включения .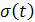

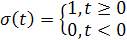
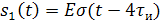
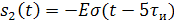
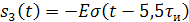
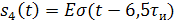
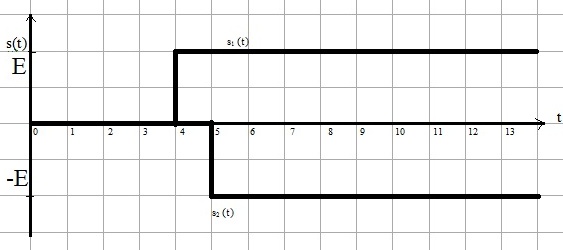
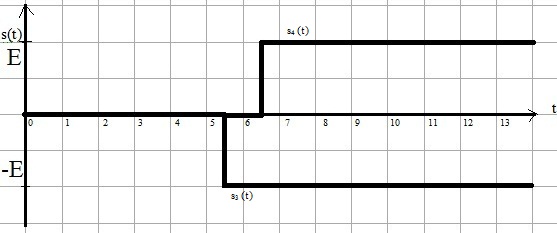
Рисунок 1.2 – Временное представление типовых составляющих аналогового сигнала

РАСЧЕТ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ АНАЛОГОВОГО СИГНАЛА

Спектральной характеристикой (или спектральной плотностью) непериодического сигнала называют комплексную функцию частоты :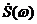

.

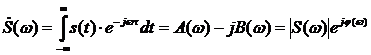1. Рассмотрим одиночный импульс нашего сигнала (рисунок 1.3).

Рисунок 1.3 – Временное представление одиночного импульса

2. Представим сигнал с помощью элементарных составляющих (рисунок 1.4).

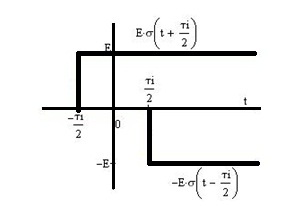
Рисунок 1.4 - Временное представление сигнала с помощью элементарных составляющих

3. Применяя прямое преобразование Лапласа, получим:

.

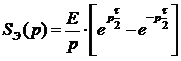4. Заменяя 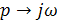, перейдем к спектральной плотности элементарной составляющей сигнала:

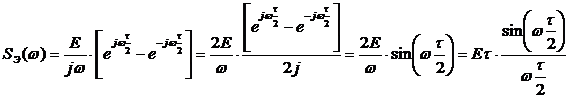
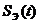5. Моделируем сигнал от (рисунок 1.4):

.

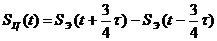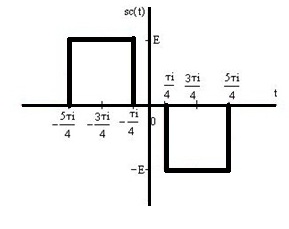
Рисунок 1.5 – Временное представление центрированного сигнала

6. Применяя прямое преобразование Лапласа, получим спектральную плотность центрированного сигнала:

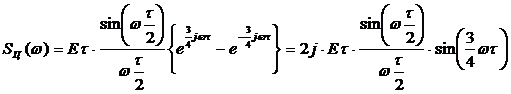
7. Возвращая 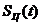в исходное место, получим конечное выражение для расчета спектральной плотности:

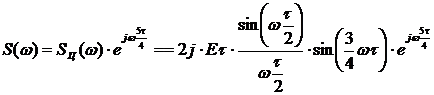
Построение частотных характеристик аналогового сигнала

Модуль комплексной спектральной плотности называют амплитудно-частотной характеристикой (АЧХ) спектра сигнала s(t). Аргумент комплексной спектральной плотности фазочастотной характеристикой (ФЧХ) спектра сигнала s(t).

Построим графики с нормированными значениями, применив замену:

t _н = t/τ_i

αt = ln10* t _н = 2,3 * t _н

ω _н = ω/α

ωτ = ω _{н *} ln 10 = ω* 2.3

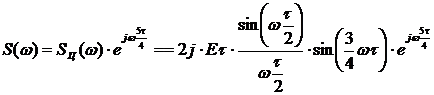
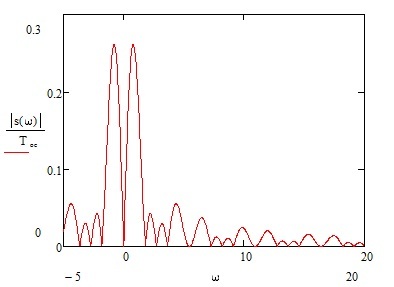
Рисунок 1.6 – АЧХ аналогового сигнала

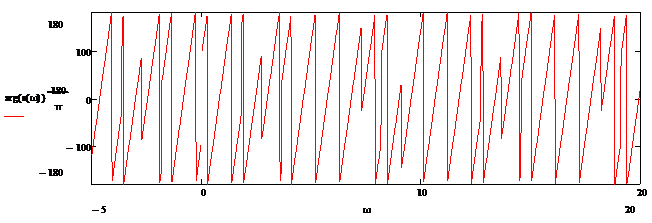
Рисунок 1.7 - ФЧХ аналогового сигнала

РАСЧЕТ И ПОСТРОЕНИЕ СПЕКТРА КОЭФФИЦИЕНТОВ КОМПЛЕКСНОГО РЯДА ФУРЬЕ

Ряд Фурье – это разложение периодического сигнала по тригонометрическим либо комплексным функциям.

Найдем коэффициенты комплексного ряда Фурье с помощью дискретизации спектральной плотности аналогового сигнала.

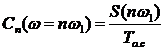
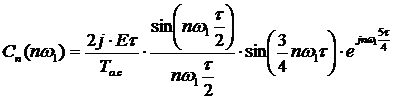, где 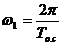- циклическая частота сигнала.

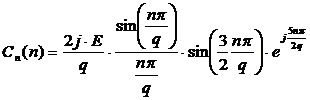, где 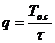– скважность.

Построим спектральные характеристики периодического сигнала.

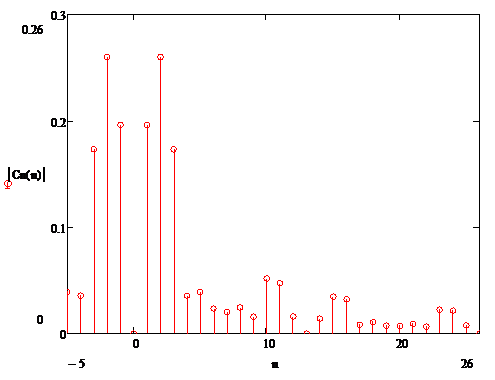
Рисунок 1.8 – Спектр амплитуд коэффициентов комплексного ряда Фурье

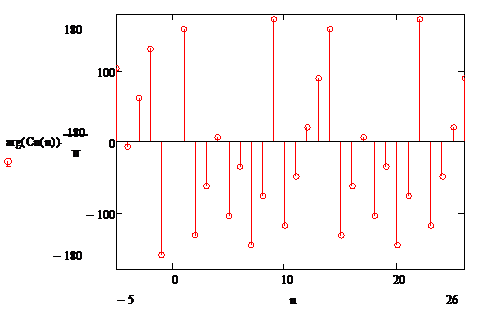
Рисунок 1.9– Спектр фаз коэффициентов комплексного ряда Фурье

Таблица 1 – Коэффициенты комплексного ряда Фурье

N	Алгебраическое представление С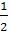n = (an-jbn)	Модуль |Cn|	Аргумент Arg(Cn)
			-
	-0.183 + j0.07	0.196
	-0.172 - j0.195	0.26	-132
	0.081 - j0.154	0.173	-62
	0.035 + j4.293*10-3	0.036
	-9.39*10-3 - j0.038	0.039	-104
	0.02 - j0.013	0.024	-35
	-0.017 - j0.012	0.02	-145
	5.869*10-3 - j0.024	0.025	-76
	-0.016 + j1.908*10-3	0.016
	-0.024 - j0.046	0.052	-118
	0.031 - j0.035	0.047	-49
	0.015 + j5.797*10-3	0.016
			-90
	-0.013 + j4.969*10-3	0.014
	-0.023 - j0.026	0.035	-132
	0.015 - j0.029	0.033	-62
	8.318*10-3 + j1.01*10-3	8.38*10-3
	-2.608*10-3 - j0.011	0.011	-104
	6.17*10-3 - j4.259*10-3	7.498*10-3	-35
	-5.862*10-3 - j4.046*10-3	7.123*10-3	-145
	2.236*10-3 - j9.071*10-3	9.342*10-3	-76
	-6.42810-3 + j7.805*10-4	6.475*10-3
	-0.011 - j0.02	0.023	-118
	0.014 - j0.016	0.022	-49
	7.337*10-3 + 2.783*10-3	7.847*10-3
			-90