Модель управления запасами «минимум-максимум»

Еще одним вариантом доработки основных моделей для усло­вий колебаний потребности в запасе является модель управления запасами «минимум-максимум». В отличие от модели с периоди­ческим пополнением запаса до постоянного уровня эта модель разработана для условий, когда издержки содер­жания запаса превышают издержки в результате дефицита. В такой ситуации наличие определенного уровня дефицита оправдано, а содержание большого запаса нежелательно. Поэтому в модели «ми­нимум-максимум» заказы производятся не в каждый заданный момент времени, как в модели с фиксированным интервалом вре­мени между заказами, а только в те заданные моменты, когда запас оказался меньшим или равным установленному минимальному уровню запаса. В случае выдачи заказа его размер определяется экспертно, чтобы поставка пополнила запас до максимального же­лательного уровня. Таким образом, данная модель работает с дву­мя уровнями запаса — минимальным и максимальным, чему и обязана своим названием.

Как и предыдущая модель с установленной периодичностью пополнения запаса до постоянного уровня, модель «минимум-мак­симум» содержит в себе элементы основных моделей управления запасами. Как и в модели с фиксированным интервалом времени между заказами, здесь используется постоянный интервал времени между возможными заказами. Из модели с фиксированным раз­мером заказа заимствована идея отслеживания некоторого поро­гового уровня, который здесь называется минимальным.

Исходные данные для расчета параметров модели «минимум- максимум» совпадают с моделью управления запасами с фиксиро­ванным интервалом времени между заказами:

1) объем потребности в запасе, единиц;

2) интервал времени между заказами, дни;

3) время выполнения заказа, дни;

4) возможная задержка поставки, дни.

Расчетными параметрами модели «минимум-максимум» явля­ются:

1) максимальный запас, единиц;

2) минимальный запас, единиц;

3) страховой запас, единиц.

Расчет максимального запаса может быть проведен по форму­лам расчета максимального желательного запаса (см. позицию 10 табл. 9.11). Роль минимального уровня запаса аналогична роли по­рогового уровня запаса в модели с фиксированным размером за­каза (см. табл. 9.12). Отличие состоит в том, что в расчете мини­мального уровня запаса следует учитывать не только ожидаемое потребление за время выполнения заказа и уровень страхового за­паса (как это делается при расчете порогового уровня запаса), но и возможное отклонение потребности от запланированной вели­чины. Порядок расчета всех остальных параметров модели «мини­мум-максимум» аналогичен расчету параметров модели с установ­ленной периодичностью пополнения запаса до постоянного уров­ня (см. табл. 9.11). Заказы выдаются в объеме, который определяется либо по известной формуле из модели с фиксирован­ным интервалом времени между заказами (см. формулу (9.9)), либо экспертно — с учетом возможного изменения потребности в запа­се в будущие периоды.

Пример 9.4. Расчет параметров модели «минимум-максимум»

Для исходных данных, использованных в примерах использо­вания основных моделей (табл. 9.2, 9.7), а также модели с установ­ленной периодичностью пополнения запаса до постоянного уров­ня (табл. 9.12) рассчитаны показатели модели «минимум-максимум» (табл. 9.14).

Максимальное потребление за время выполнения заказа (см. позицию 8 табл. 9.14) рассчитано исходя из предположения, что ожидаемое потребление за время выполнения заказа может быть увеличено на стандартное отклонение спроса по данным прошло­го периода, равное 2 единицам. Тогда максимальное потребление за время выполнения заказа будет равно МП = (4 + 2) • (4 + 1) = 30.

Таблица 9.14 - Пример расчета параметров модели «минимум-максимум»

Ns п/п	Показатель	Значение
	Объем потребности, единиц
	Интервал между заказами, дни
	Время выполнения заказа, дни
	Возможная задержка поставки, дни
	Ожидаемое дневное потребление, единиц/день
	Ожидаемое потребление за время выполнения заказа, единиц
	Максимальное потребление за время выполнения заказа, единиц
	Страховой запас, единиц
	Минимальный уровень запаса, единиц
	Максимальный запас, единиц

Страховой запас (см. позицию 9 табл. 9.14) будет равен, учиты­вая наличие и задержки поставки (см. позицию 4 табл. 9.14) и воз­можное отклонение спроса на стандартное отклонение в 2 едини­цы как разницу максимального потребления за время выполнения заказа (см. позицию 8 табл. 9.14) и ожидаемого потребления за вре­мя выполнения заказа (см. позицию 4 табл. 9.14). z_s = 30 - 16 = 14.

Минимальный уровень запаса (см. позицию 10 табл. 9.14) оп­ределен на основе формулы расчета порогового уровня запаса при учете возможного увеличения потребности на величину стандарт­ного отклонения в 2 единицы (см. позицию 10 табл. 9.1): ПУ= 14+ (4+ 2)-4 = 38.

Максимальный запас (см. позицию 11 табл. 9.14) определен на основе формулы расчета максимального желательного запаса при учете возможного увеличения потребности на величину стандарт­ного отклонения в 2 единицы (см. позицию 10 табл. 9.11):

М3= 14+ (4+ 2)- 10 = 74.

Иллюстрация движения запаса по методике «минимум-макси­мум» приведена в табл. 9.15.

Первоначально запас находится на максимальном уровне. Предположим, что заказы выполняются на 10-й день. В первый день заказ не выдается, так как запас находится выше заданного минимального уровня (см. позицию 8 табл. 9.14). До 10-го дня те­кущий контроль уровня запаса не проводится. На 10-й день уро­вень запаса равен минимальному, требуется выдать заказ, который в данном примере определяется по формуле определения размера заказа в модели с фиксированным размером заказа = 74 - 38 + 16 = 52.

Сделанный заказ выполняется через четыре дня и учитывается на 14-й день. Вопрос о выдаче следующего заказа рассматривается на 20-й день. Текущий уровень запаса равен 24 единицам, что ниже минимально допустимого уровня; следовательно, заказ должен быть сделан в объеме

Q₂ = 74 - 24 + 16 = 66 и т.д.

Таблица 9.15 - Расчет уровней запаса при колебании потребности в запасе и наличии задержек поставок при основных параметрах табл. 9.12

Дни	Запас	Расход	Приход	Размер заказа
День 1
День 2
День 3
День 4
День 5
День 6
День 7
День 8
День 9
День 10
День 11
День 12
День 13
День 14
День 15
День 16
День 17
День 18
День 19
День 20
День 21
День 22
День 23
День 24
День 25
День 26
День 27
День 28
День 29
День 30
День 31
День 32
День 33
День 34
День 35
День 36
День 37
День 38
День 39
День 40
День 41
День 42
День 43
День 44
День 45
День 46
День 47
День 48
День 49
День 50
День 51
День 52
День 53
День 54
День 55
День 56
День 57
День 58
День 59
День 60

Заказ не выдается на 50-й день, так как запас находится на уров­не, превышающем минимальный уровень. Иллюстрация движения запаса поданным табл. 9.15 представлена на рис. 9.13.

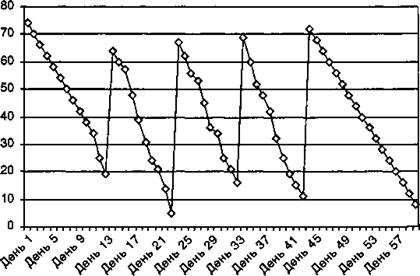
Рис. 9.13. Иллюстрация движения запаса при колебании потребности в запасе по параметрами табл. 9.15

Как видно из рис. 9.13, обеспечение потребности запасом после корректировки расчетов основных параметров (максимального и минимального уровня запаса, а также страхового запаса) модели «минимум-максимум» дает результат, сравнимый с результатом ис­пользования модели с установленной периодичностью пополнения запаса до постоянного уровня. В течение длительного пе­риода времени дефицита удается избежать, пользуясь определен­ными аналитическими расчетами и предположением, что задержек поставок не было. В отличие от результатов производных моделей использование основных моделей управления запасами в условиях колебания потребности приводит к устойчивому дефициту запаса в периоды, близкие к получению поставок.