Вычисление угловой скорости и углового ускорения тела при плоском движении

Как видно из выше изложенного, при вычислении скоростей и ускорений точек тела при плоском движении важно уметь найти угловую скорость и угловое ускорение тела. Остановимся на этом отдельно.

Основные способы вычисления угловой скорости

1. Если заданы кинематические уравнения плоского движения тела (41),то угловую скорость можно вычислить согласно ее определению

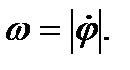
2. Если известны скорость какой-либо точки тела и положение МЦС, то угловая скорость может быть найдена по формуле (48)

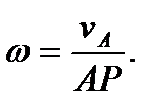
Направление угловой скорости в этом случае определяется направлением вектора 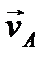(см. рис. 46).

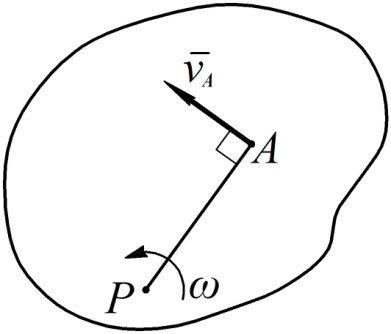
Рис. 46

3. Угловая скорость может быть также найдена, если известна скорость при относительном вращении какой-либо точки В вокруг полюса А. В этом случае

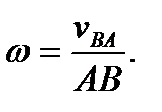
Направление угловой скорости здесь должно быть согласовано с направлением вектора относительной скорости 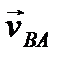(см. рис. 47).

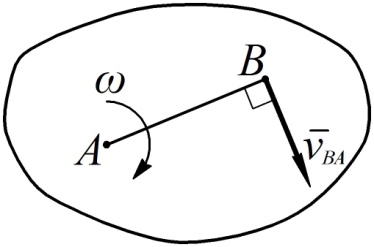
Рис. 47

Основные способы вычисления углового ускорения

1. Если заданы кинематические уравнения движения тела (41), то угловое ускорение найдется согласно определению

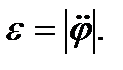
2. Если угловая скорость была найдена по формуле (48)

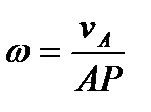
и расстояние от точки А до мгновенного центра скоростей не изменяется при движении тела (AP=const), то, дифференцируя по времени последнее выражение для углового ускорения, получим

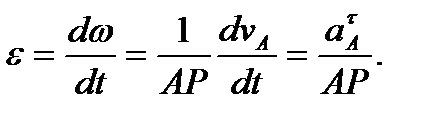
Проиллюстрируем этот способ нахождения углового ускорения тела примером. Пусть колесо катится по горизонтальной поверхности без скольжения. Для центра колеса С заданы скорость 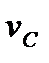и ускорение 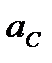(см. рис. 48).

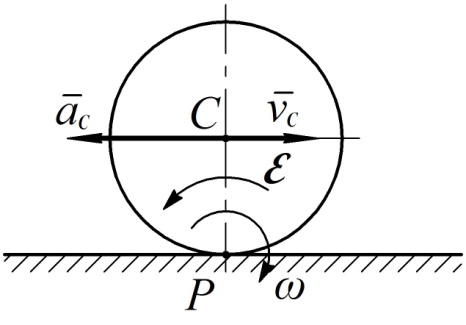
Рис. 48

Угловая скорость колеса в этом случае найдется по формуле

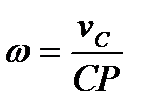
и в соответствии с направлением вектора 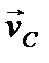будет направлена по часовой стрелке. Расстояние от точки С до мгновенного центра скоростей при движении колеса не меняется и равно радиусу колеса CP=R. Тогда угловое ускорение колеса можно найти по формуле

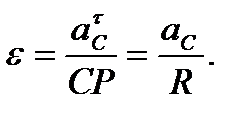
Так как по условию качение колеса является замедленным, то направление углового ускорения будет противоположно направлению угловой скорости (см. рис. 48).

3.Если известно тангенциальное ускорение какой-либо точки В тела при ее относительном вращении вокруг полюса А 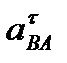, то угловое ускорение тела найдется по формуле

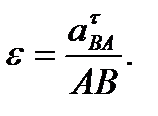
Этот способ вычисления ε использовался при нахождении углового ускорения шатуна АВ в примере 7.

Раздел 2. СТАТИКА

Статика – это раздел механики, в котором изучается равновесие материальных объектов под действием приложенных сил.

Глава 1. ВВЕДЕНИЕ В СТАТИКУ

Основные понятия

Силой называется векторная величина, характеризующая механическое воздействие одного материального объекта на другой.

Сила характеризуется точкой приложения, направлением действия и численной величиной (модулем).

Совокупность сил, действующих на выбранный материальный объект, называется системой сил.

На рис. 49 изображена система сил, приложенных к некоторому телу.

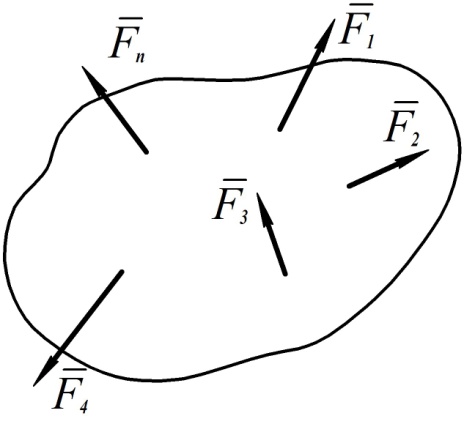
Рис. 49

Будем обозначать систему сил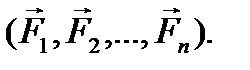

Две системы сил называются эквивалентными, если, будучи приложенными к твердому телу по отдельности, они сообщают ему одно и то же движение из состояния покоя. Эквивалентность систем сил обозначается знаком :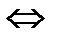

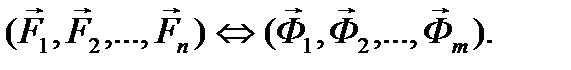
Система сил называется уравновешенной (или эквивалентной нулю), если она, будучи приложенной к твердому телу, не сообщает ему движения из состояния покоя. Уравновешенную систему сил обозначают следующим образом:

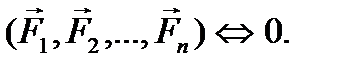
Главным вектором системы сил (обозначается 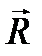) называется вектор, равный геометрической сумме всех сил, входящих в систему:

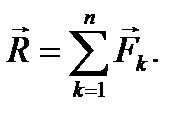(55)

На рис. 50 показано геометрическое построение главного вектора системы

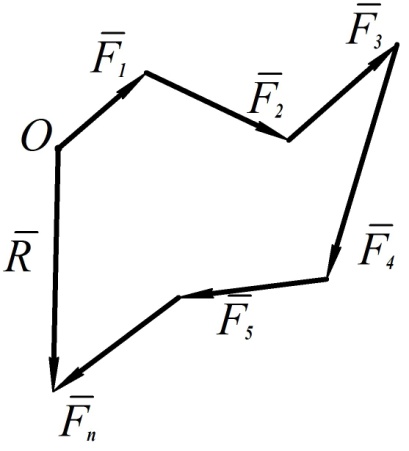
Рис. 50

сил. На практике такой способ неудобен и для нахождения главного вектора равенство (55) записывают в проекциях на выбранные оси координат

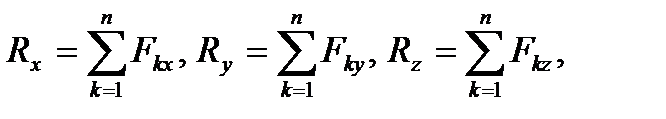
после чего величину главного вектора вычисляют по теореме Пифагора

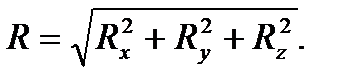
Равнодействующей силой данной системы сил (обозначается 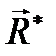) называется сила, эквивалентная этой системе сил:

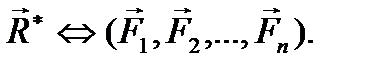
Отметим, что не всякая система сил имеет равнодействующую.

Тело называется свободным, если ничто не препятствует его перемещению в пространстве.

В противном случае тело называется несвободным.

Материальные объекты, ограничивающие перемещение несвободного тела, называются связями.

Силы, с которыми связи действуют на несвободное тело, называются реакциями связей или пассивными силами.

Остальные силы, не являющиеся реакциями связей, называются активными силами.

Активные силы могут сообщать свободному телу движение, они имеют определенный источник действия, не зависят наложенных связей и обычно считаются известными при решении задач.

Реакции связей зависят от активных сил, действующих на несвободное тело, они могут изменять свою величину и направление при изменении активных сил.

Аксиомы статики

Все основные методы изучения движения и равновесия тел в теоретической механике могут быть строго доказаны математически, исходя из нескольких основных положений, называемых аксиомами. Сами аксиомы сформулированы на основании многовекового опыта человечества. Далее приведем формулировки аксиом статики и дадим необходимые пояснения.

П е р в а я а к с и о м а . Система из двух сил, равных по величине и направленных в противоположные стороны вдоль одной прямой, является уравновешенной.

Эта аксиома справедлива для сил, приложенных к одному абсолютно твердому телу.

В т о р а я а к с и о м а. Механическое состояние тела не изменится, если к действующей на него системе сил добавить или изъять уравновешенную систему сил.

Исходя из приведенных выше двух аксиом, докажем следствие.

Любую силу, не нарушая ее действия на абсолютно твердое тело, можно переносить вдоль линии действия силы.

Рассмотрим абсолютно твердое тело, на которое в точке А действует сила 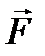. Возьмем уравновешенную систему сил 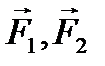, равных по величине силе 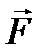и направленных в противоположные стороны по линии действия силы 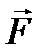. Приложим обе эти силы в точке В на линии действия силы 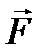(см. рис. 51).

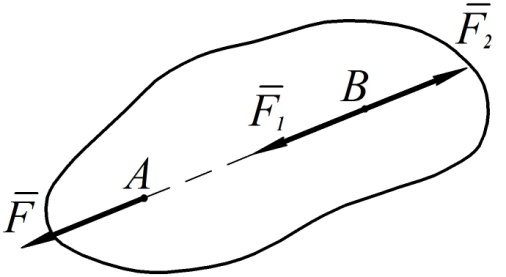
Рис. 51

Тогда по второй аксиоме

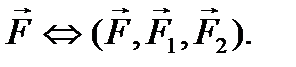
Но по первой аксиоме силы 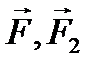образуют уравновешенную систему и по второй аксиоме их можно отбросить. В результате получим

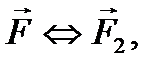
что и доказывает следствие.

Т р е т ь я а к с и о м а (закон равенства действия и противодействия). Два тела взаимодействуют с другом с силами, равными по величине и противоположно направленными вдоль одной прямой.

Заметим, что эти силы не будут уравновешенными, так как они приложены к разным телам.

Ч е т в е р т а я а к с и о м а (аксиома параллелограмма сил). Система из двух сил, приложенных в одной точке тела, имеет равнодействующую силу, равную геометрической сумме двух данных сил.

Эту аксиому можно выразить формулой 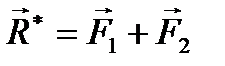и пояснить рисунком

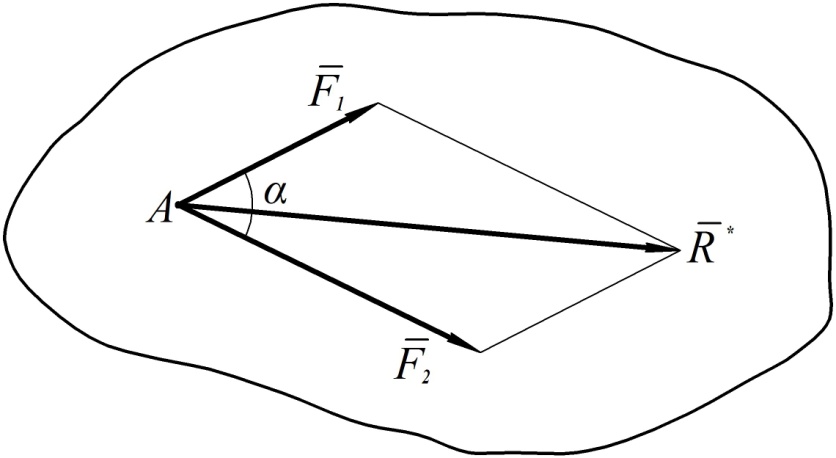
Рис. 52

Величину равнодействующей можно вычислить по формуле

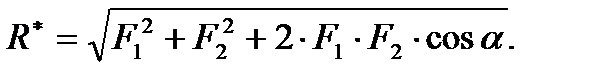
Данная аксиома допускает и обратное утверждение: силу можно по правилу параллелограмма разложить бесчисленным множеством способов на две силы.

При этом составляющие силы могут располагаться в любой одной плоскости, проходящей через линию действия разлагаемой силы.

П я т а я а к с и о м а (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если связи мысленно отбросить и заменить их действие соответствующими реакциями.

Ш е с т а я а к с и о м а (аксиома отвердевания). Равновесие механической системы не нарушится от наложения новых связей. В частности, равновесие деформируемого тела не нарушится, если оно станет абсолютно твердым.

При этом под механической системой подразумевается выделенная совокупность материальных точек и тел.