Свойства вероятности. Теорема сложения вероятностей несовместных событий
Определение. Суммой событий A и B (обозначается A+B или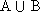 
) называется событие, которое заключается в том, что произойдет хотя бы одно из двух событий A или B.
Определение. Произведением событий A и B (обозначается AB или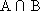 
) называется событие, которое заключается в том, что произойдут оба события A и B.
Определение. Событие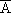 
называется противоположным событию A, если:
- A и 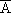несовместны: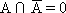
- и в сумме образуют полную группу:
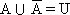
Пример 12.1. В опыте с одним подбрасыванием кубика полную группу образуют 6 исходов: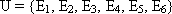 
. Пусть события A, B и C заключаются в следующем:
Найдем суммы и произведения различных пар этих событий, события, противоположные данным, а также их вероятности.
Решение.
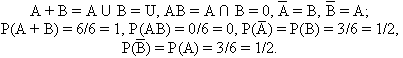
При нахождении суммы двух событий сначала перечислим все исходы, благоприятствующие одному из них, а затем добавим те исходы второго, которые еще не перечислили:
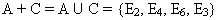
При нахождении произведения перечислим общие исходы двух событий:
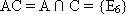. Чтобы найти событие, противоположное данному, надо перечислить те исходы из полной группы, которые не попали в число благоприятствующих данному событию: 
.
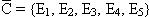Вероятность находится по определению - число исходов, благоприятствующих данному событию, делится на общее число равновозможных исходов, образующих полную группу: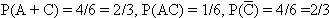 
.
Пример 12.2. Вероятность того, что стрелок при одном выстреле выбивает 10 очков, равна 0,1, вероятность выбить 9 очков равна 0,3, вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.
Решение.Опыт состоит в одном выстреле по мишени. Пусть событие A состоит в том, что стрелок выбивает 10 очков, событие B - стрелок выбивает 9 очков и событие C - стрелок выбивает число очков, меньшее или равное 8. По условию задачи, P(A)=0,1, P(B)=0,3, P(C)=0,6. Так как максимальное число выбитых очков равно 10, то событие, состоящее в том, что при одном выстреле стрелок выбьет не менее 9 очков равносильно тому, что он выбьет 9 или 10 очков. Следовательно, нас интересует вероятность события A+B: P(A+B)-?
1 способ. Решение задачи состоит в следующем. События A и B несовместны, так как у них нет общих исходов. Поэтому применима теорема сложения вероятностей несовместных событий:
P(A + B) = P(A) + P(B) + 0,1 + 0,3 = 0,4
Ответ: P(A+B)=0,4.
2 способ. Обозначим через D искомое событие - стрелок выбил больше или равно 9 очков. Событие D является противоположным для события C: D=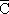 
, так как они несовместны и в сумме образуют полную группу. По свойству вероятности противоположного события:
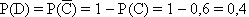
Ответ: P(D)=0,4.
СПИСОК ИНФОРМАЦИОННЫХ РЕСУРСОВ
1. Савина Л.Н., Попырев А.В. «КОМБИНАТОРИКА» издательство Елабужский государственный педагогический институт 1999г2. Халамайзер А. Я. «Математика? – Забавно!» издание автора 1989г3. Гнеденко Б.В. Курс теории вероятностей. - М.: УРСС, 2005.4. Башарин Г.П. Введение в теорию вероятностей. - М.: Изд-во УДН, 1990.
5. Феллер В. Введение в теорию вероятностей и ее приложения. Т.1. – М.: Мир, 1984.6. А.Г.Мордкович, П.В. Семёнов. События, вероятности, статистическая обработка данных. 7-9 класс.7. В. П. Чистяков. Курс теории вероятностей. М.,1982.
8. А. А. Боровков. Теория вероятностей. М.,1986.9. http://do.rksi.ru/library/courses/ms/tema1_6.dbk10. Б. А. Севастьянов, В. П. Чистяков, А. М. Зубков. Сборник задач по теории вероятностей. М.,1986.
11. http://www.cultinfo.ru/fulltext/1/001/008/063/207.htm 12. http:\www.mathclub.zala.ru/0921.html 13. http://www.ezi.ru/1/36/533.htm