I. Определение уравнений линейной регрессии
Регрессия является линейной, если уравнение имеет вид:
n
y=b+Smixi . (1)
i=1
Для получения уравнения регрессии необходимо:
n определить значения b, mi;
n оценить достоверность полученного уравнения.
Эту задачу можно решить используя табличную функцию Excel ЛИНЕЙН( ), формат которой имеет вид:
=ЛИНЕЙН(интервал_значений_y; блок_значений_xi; константа; статистика).
Ввод константы и статистики обеспечивает представление результатов вычислений в различных вариантах:
| ИСТИНА | ЛОЖЬ | |
| Константа | b¹0 | b=0 |
| Статистика | Оценка достоверности | Оценки нет |
Если константу не назначать, то результат будет представлен в такой же форме, как и при вводе ИСТИНА, т.е. b¹0. Если не назначать статистику, то результат будет таким же, как при вводе ЛОЖЬ, т.е. данные для оценки достоверности представлены не будут.
Уравнение линейной регрессии будем определять для исходных данных, приведенных на рис. 3. В этой таблице указаны два технических параметра:
x1 - производительность (количество операций в час);
x2 - характеристика качества (время наработки на отказ в днях);
и один экономический:
y - цена аппаратуры (в тыс. руб.).
Требуется определить уравнение регрессии, устанавливающее зависимость цены от технических параметров. Для этого необходимо выполнить следующее:
1. ввести исходные данные на 12 рабочий лист (Линейная) вашей книги , как показано на рис.1:
n блок значений x в B4:C9;
n интервал значений y в D4:D9.
2. Определить минимальные и максимальные значения переменных:
n в ячейку B11 введите функцию =МИН(B4:B9);
n в ячейку B12 введите функцию =МАКС(B4:B9);
n скопировать B11:B12 в C11:C12.
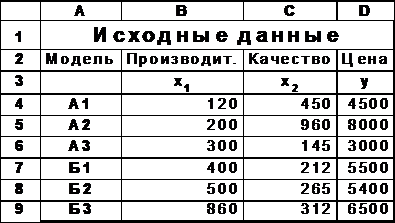
Рис.3. Исходные данные для расчета
3. Ведите функцию ЛИНЕЙН(), в ячейку B14. Для этого выполните следующее.
n Выделите интервал B14:D18, в котором строк всегда 5, а столбцов - n+1, т.е. 2+1=3.
n Не снимая выделения наберите функцию =ЛИНЕЙН(D4:D9;B4:C9; ИСТИНА; ИСТИНА).
n Нажмите одновременно клавиши <Shift>+<Ctrl> и <Enter>. На экране будет результат вычислений в ячейках B14:D18, содержимое которых представлено на рис. 4.
n Округлите полученные результаты до двух знаков после запятой.
 |
Рис. 4. Результаты выполнения функции ЛИНЕЙН( )
Смысл полученных величин показан на рис. 5. Величины b, m1,..., mn-1, mn - неизвестные величины в уравнении линейной регрессии (1).
| .mn | .mn-1 | ... | .m1 | b |
| s[mn] | s[mn-1] | s[m1] | s[b] | |
| R2 | s[g] | |||
| Fрасч | df | |||
| Ssreg | SSresid |
Рис. 5. Обозначение величин
Таким образом, искомое уравнение регрессии имеет вид
y=1721,33+3,88*X1+5,69*X2.
Полученное уравнение описывает зависимость экономического параметра - цены, от технических - производительности и характеристики качества. При этом уравнение регрессии справедливо только в пределах определенных минимальных и максимальных значений переменных
120<= X1<=860; 145<= X2<=960,
на базе которых оно и было получено.
Далее в интервале B14:D18 (рис.4) представлены величины, необходимые для оценки достоверности полученного уравнения регрессии:
s[mi], s[b] - средние квадратичные отклонения полученных значений,
R2 - величина, характеризующая достоверность,
df - число степеней свободы, определяемое по формуле
df=k-(n+1), (2)
где k - число строк в таблице исходных данных (k=6),
n - число аргументов (n=2).
Тогда df=6-(2+1)=3.
SSreg- регрессионная сумма квадратов,
SSresid - остаточная сумма квадратов.
После определения уравнения регрессии целесообразно оценить достоверность полученной зависимости. Оценка достоверности Y от Xi производится по величине R2, которая для решаемой задачи находится в ячейке B16 и равна 0,88. При R2=1 имеется функциональная зависимость, при R2=0 зависимость отсутствует (несмотря на найденные значения b и mi). Полученное значение R2=0,88 достаточно высокое и подтверждает достоверность наличия зависимости между Y и Xi.
Кроме того, можно оценить достоверность самой величины R2 с помощью функции FРАСП( ). Достоверность значений b и mi можно определить с помощью статистической функции СТЬЮДРАСП( ).
