Практической работы №1 и №2 по теме

«Действия над комплексными числами в алгебраической форме»,

«Решение уравнений, неравенств и систем уравнений и неравенств»

I.Определение. Биквадратным уравнением называется уравнение четвертой степени, содержащее только четные степени неизвестного.

Метод решения: введение новой переменной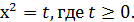

Тогда относительно переменной t получаем квадратное или неполное квадратное уравнение. Решаем его, а затем возвращаемся к исходной переменной х и находим её.

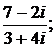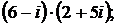Задание: Выполнить действия над комплексными числами в алгебраической форме записи: а) б) в) .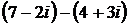

Решение:

а)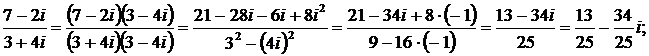

б)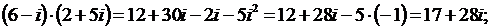

в) .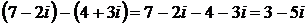

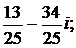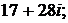Ответ: а) б) в) .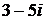

Методические указания и примеры типового расчёта

Практической работы №3 по теме

«Вычисление пределов функции в точке и на бесконечности»

Теория

Теоремы о пределах функции в точке и на бесконечности:

1) О пределе суммы функций:
;

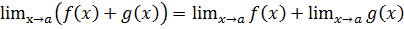2) О пределе разности функций:

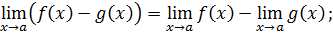
3) О пределе произведения функции:
;

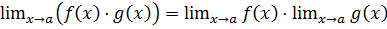4) О пределе деления частного двух функций:
;

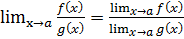5) Постоянный множитель можно вынести за знак предела:
.

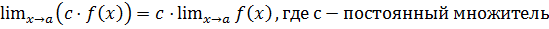Правило №1.Чтобы раскрыть понятие неопределённости вида 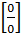, нужно и числитель и знаменатель разложить на простейшие множители и сократить дробь, тогда неопределённость исчезнет и можно применять теоремы о пределах.

Правило №2.Чтобы избавиться от неопределённости вида 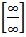, нужно одновременно и числитель и знаменатель дроби разделить на 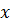в наивысшей степени, тогда неопределённость исчезнет и можно применять теоремы о пределах.

Пример 1.Вычислить предел функции:

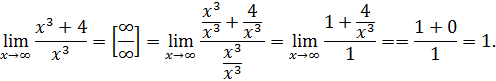
Методические указания и примеры типового расчёта

Практической работы №4 по теме

«Решение показательных и логарифмических уравнений и неравенств»

При решении уравнений и неравенств используют основные свойства логарифмов:

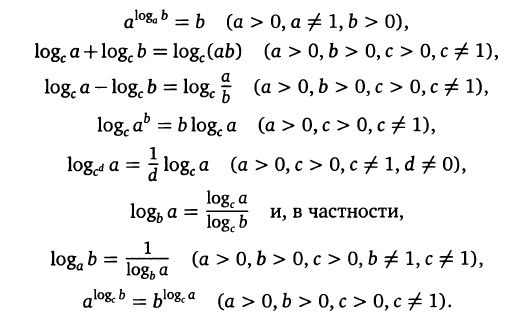
Методические указания и примеры типового расчёта

Практической работы №5 по теме

«Тригонометрические функции: вычисление значений функции, преобразование выражений, доказательство тождеств»

Теория

Основные соотношения между функциями одного и того же угла:

; ;

; ; ; ; .

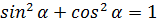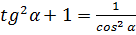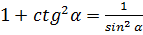
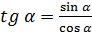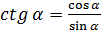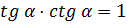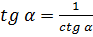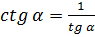Формулы двойного угла: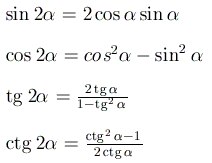

Знаки тригонометрических функций по четвертям:

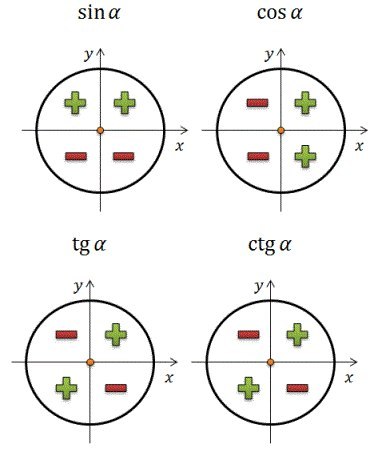
Задание 1

Дано: .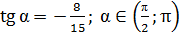

Найти: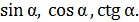

Решение:

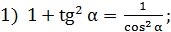тогда 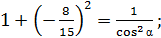отсюда находим

;
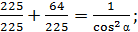
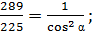
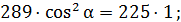
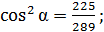
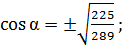
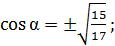
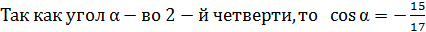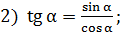тогда

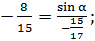
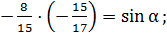
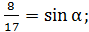
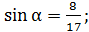
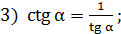тогда

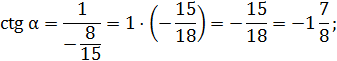
Ответ: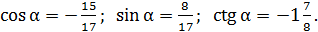

Задание 2

Дано: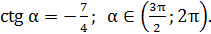

Найти: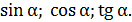

Решение:

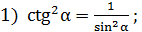тогда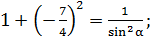

.

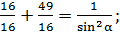
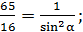
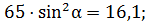
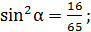
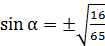Так как, α- угол 4-й четверти, то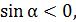

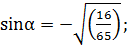или 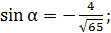вычисляем с точностью до сотых

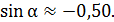
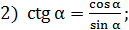тогда 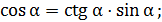подставляем числовые значения

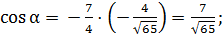вычисляем с точностью до сотых

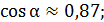
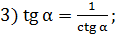вычисляем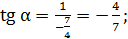

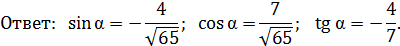
Задание 3

I. Привести угол к табличному и вычислить значения тригонометрической функции:

1)

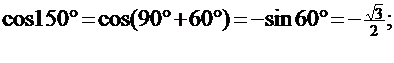
2)

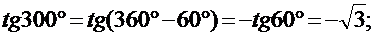
3)

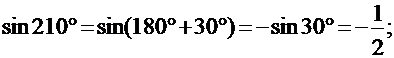
4)

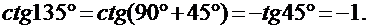
II. Не изменяя название тригонометрической функции привести к острому углу:

1)

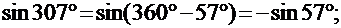
2)

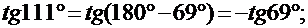
3)

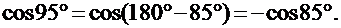
III. Используя свойства нечетности, четности, периодичности тригонометрических функций вычислить:

1) Вычислить: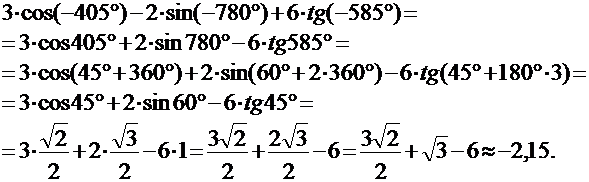

2)

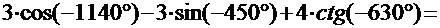
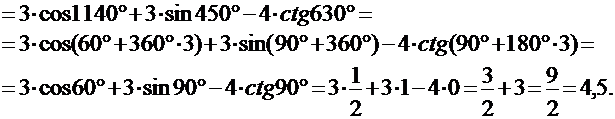
3) Вычислить значение тригонометрического выражения: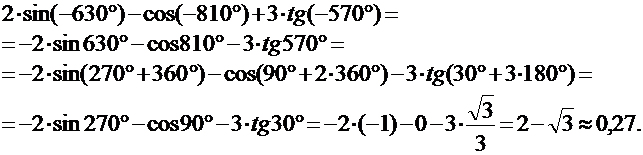

4) Вычислить:

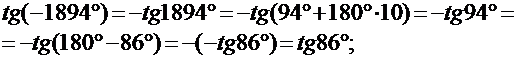
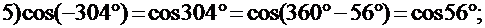
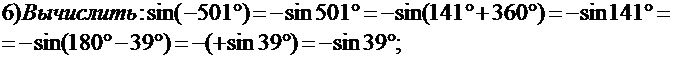
7) Вычислить: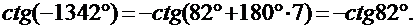

Методические указания и примеры типового расчёта