Построение нормальной кривой по опытным данным

Один из способов построения нормальной кривой по данным наблюдений состоит в следующем.

1) Найти 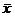и .

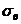2) Найти ординаты (выравнивающие частоты) теоретической кривой по формуле , где п – сумма наблюдаемых частот (объем выборки), h – разность между двумя соседними вариантами, 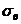– выборочное среднее квадратическое отклонение, 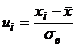, –середина 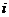-го частичного интервала.

3) строят точки 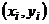в прямоугольной системе координат и соединяют их плавной кривой.

Замечание.Близость выравнивающих частот к наблюдаемым подтверждает правильность допущения о том, что обследуемый признак распределен нормально.

Пример 3.1.Построить кривую по данному распределению:

Выяснить, насколько обоснованной является гипотеза о том, что построенная кривая является нормальной, а данное распределение является выборкой из нормально распределённой генеральной совокупности.

Решение. 1) Вычислим выборочную среднюю, выборочное СКО и выравнивающие частоты. Для этого составим расчётную таблицу.

№
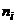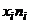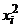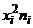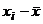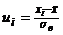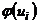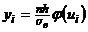1.
2.
3.
4.
5.
6.
7.
8.
9.

2) Построим графики эмпирического распределения (по наблюдаемым частотам) и теоретического (по вычисленным выравнивающим частотам).

Сравнение графиков наглядно показывает что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

3) Проверим правило трёх сигм для данного распределения. Для этого с помощью расчётной таблицы выясним, для скольких наблюдаемых значений выполняется неравенство .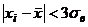

Замечание. В примере 3.1 наблюдаемые значения являются равноотстоящими. Если при решении задачи окажется, что наблюдаемые значения не являются равноотстоящими, то их нужно сделать таковыми, пользуясь замечанием 4 п. 1.1.

Оценка отклонения эмпирического распределения от нормального.

Асимметрия и эксцесс

Для оценки отклонения эмпирического распределения от нормального используют различные характеристики, к числу которых относятся асимметрия и эксцесс. Определения этих характеристик аналогичны определениям асимметрии и эксцесса теоретического распределения.

Асимметрия эмпирического распределенияопределяется равенством: 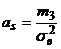, где 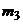– центральный эмпирический момент третьего порядка.

Эксцесс эмпирического распределенияопределяется равенством: 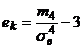, где 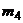– центральный эмпирический момент четвертого порядка.

Пример 3.1 (продолжение).Найдём асимметрию и эксцесс эмпирического распределения примера 3.1.

Решение. Центральные эмпирические моменты вычисляются по формуле:

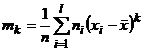
Составим расчётную таблицу.

№
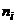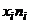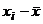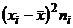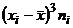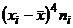1.
2.
3.
4.
5.
6.
7.
8.
9.

Асимметрия распределения равна:

Эксцесс распределения равен:

Вывод.

Замечание. В случае малых выборок дополнительно к оценкам асимметрии и эксцесса требуется находить точности этих оценок (см. [14]).

Сравнение исправленной выборочной дисперсии