Эмпирические и теоретические частоты

Дискретное распределение

Рассмотрим дискретную случайную величину X, закон распределения которой неизвестен. Пусть произведено п испытаний, в которых величина X приняла 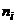раз значение ( 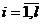), причем .

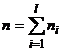Определение 6. Эмпирическими частотами называют фактически наблюдаемые частоты .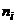

Пусть имеются основания предположить, что изучаемая величина X распределена по некоторому определенному закону. Для того чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты наблюдаемых значений, т. е. находят теоретически сколько раз величина X должна была принять каждое из наблюдаемых значений, если она распределена по предполагаемому закону.

Определение 6. Выравнивающими (теоретическими) называют частоты 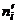, найденные теоретически (вычислением).

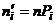Замечание. Выравнивающая частота наблюдаемого значения дискретного распределения равна произведению числа испытаний на вероятность этого наблюдаемого значения: , где п –число испытаний, 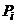– вероятность наблюдаемого значения , вычисленная при допущении, что X имеет предполагаемое распределение. Эта формула следует из теоремы о математическом ожидании числа появлений события в независимых испытаниях (см. биномиальное распределение).

Пример 1.1.В результате эксперимента, состоящего из п=520 испытаний, в каждом из которых регистрировалось число появлений некоторого события, получено следующее эмпирическое распределение:

набл. знач.
эмп. частота

Найти выравнивающие частоты 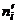в предположении, что случайная величина X (генеральная совокупность) распределена по закону Пуассона.

Решение. Известно, что параметр 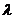, которым определяется распределение Пуассона, равен математическому ожиданию этого распределения. Поскольку в качестве оценки математического ожидания принимают выборочную среднюю, то и в качестве оценки 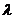можно принять выборочную среднюю .

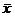Вычислим: =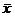

Следовательно, можно принять = .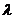

Таким образом, формула Пуассона 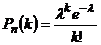принимает вид:

Пользуясь этой формулой, найдем вероятности и теоретические частоты. Результаты вычислений запишем в расчётную таблицу.

Вероятности:

Теоретические частоты:

Набл. знач.
Эмп. частота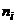
Вероятность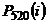
Теор. частота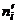

Вывод.Сравнительно небольшое расхождение эмпирических и выравнивающих частот подтверждает предположение, что рассматриваемое распределение подчинено закону Пуассона.

Вычислим =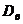

Это служит еще одним подтверждением сделанного предположения, поскольку для распределения Пуассона .

Непрерывное распределение

В случае непрерывного распределения, вероятности отдельных возможных значений равны нулю. Поэтому весь интервал возможных значений делят на k непересекающихся интервалов и вычисляют вероятности 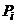попадания X в 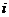-й частичный интервал, а затем, как и для дискретного распределения, умножают число испытаний на эти вероятности, т.е. 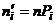, где п –число испытаний, 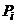– вероятность попадания X в 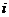-й частичный интервал, вычисленная при допущении, что X имеет предполагаемое распределение.

Замечание.В частности, если имеются основания предположить, что случайная величина X (генеральная совокупность) распределена нормально, то выравнивающие частоты могут быть найдены по формуле: 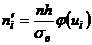, (3.1)

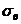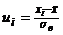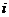где п – число испытаний (объем выборки), h — длина частичного интервала, – выборочное среднее квадратическое отклонение, , –середина -го частичного интервала, 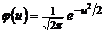– нормированная плотность нормального распределения.

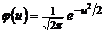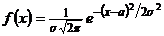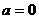Доказательство.1)Функция получается из плотности нормального распределения при и 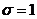после замены переменной 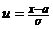. Отсюда следует, что .

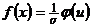2)Если математическое ожидание а и среднее квадратическое отклонение 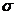неизвестны, то в качестве оценок этих параметров принимают соответственно выборочную среднюю 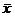и выборочное среднее квадратическое отклонение 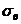.Тогда 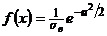, где .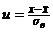

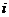3) Пусть –середина -го частичного интервала (на которые разбита совокупность всех наблюдаемых значений нормально распределенной случайной величины X) длиною h. Тогда вероятность попадания X в этот интервал приближенно равна произведению длины интервала на значение дифференциальной функции 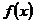в любой точке интервала и, в частности, при 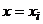: 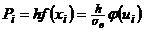. Следовательно, выравнивающая частота 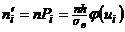, где 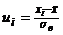.