Свойства выборочного коэффициента корреляции

1. Абсолютная величина выборочного коэффициента корреляции не превосходит единицы: .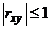

2. Если 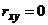и выборочные линии регрессии – прямые, то и не связаны линейной корреляционной зависимостью.

Замечание. Если 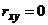, то признаки и могут быть связаны нелинейной корреляционной или функциональной зависимостью или не связаны совсем.

3.Если 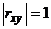, то наблюдаемые значения признаков связаны линейной функциональной зависимостью.

4.С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при 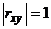переходит в функциональную зависимость.

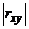Замечание 1. Выборочный коэффициент корреляции характеризует тесноту (силу) линейной связи между признаками и в выборке: чем ближе к 1, тем связь сильнее; чем ближе 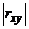к 0, тем связь слабее.

Замечание 2. Предположим, что связь между признаками и установлена и является линейной. Если при этом 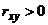, то связь является положительной (с увеличением величина увеличивается, и наоборот, с увеличением увеличивается и ); если же 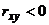, то связь является отрицательной (с увеличением величина уменьшается, и наоборот, с увеличением уменьшается и ).

Замечание 3. Чтобы проверить гипотезу о существовании связи между признаками и всей генеральной совокупности, вычисляют значение 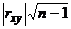. Если 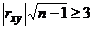, то связь между случайными величинами и достаточно вероятна (гипотеза о существовании связи подтверждается). Если 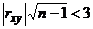, то гипотеза о существовании связи необоснованна.

Замечание 4. Если выборка имеет достаточно большой объем и является репрезентативной, то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть перенесено и на генеральную совокупность. В частности, для оценки коэффициента корреляции 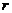нормально распределенной генеральной совокупности (при 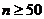) можно воспользоваться формулой: .

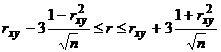Алгоритм построения уравнений линий линейной регрессии

1) По исходной таблице значений и вычислить 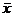, , 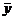, , 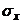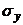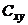и .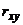

2) Проверить гипотезу о существовании связи между и (вычислить значение 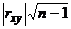; если 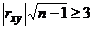, то гипотеза о существовании связи подтверждается; если 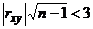, то гипотеза о существовании связи необоснованна). При необходимости оценить тесноту связи.

3) Составить уравнения обеих линий регрессии и изобразить графики этих уравнений.

Пример 1. Отыскание выборочного уравнения прямой линии регрессии по несгруппированным данным

По данным 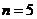наблюдений получена таблица значений величин и . Найти выборочные уравнения прямых линий регрессии на и на . Построить эти прямые. Найти выборочный коэффициент корреляции. Оценить тесноту и обоснованность связи.

X	1,0	1,5	3,0	4,5	5,0
Y	1,25	1,4	1,5	1,75	2,25

Решение. 1) Построим расчетную таблицу.

№

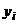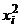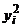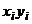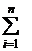Отсюда

2) Так как выборочный коэффициент корреляции близок к 1, то линейная связь между признаками и тесная; , следовательно, связь признаками и положительная. Вычислим , следовательно, связь между признаками и у всей генеральной совокупности маловероятна (это может объясняться и малым объемом выборки, т. е. выборка не репрезентативна).

3) Составим выборочные уравнения прямых линий регрессии на и на : Выборочное уравнение прямой линии регрессии на имеет вид:

или

.

Выборочное уравнение прямой линии регрессии на имеет вид:

, или

.

При большом числе наблюдений одно и то же значение 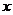может встретиться 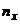раз, одно и то же значение 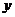может встретиться 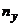раз, одна и та же пара чисел может встретится 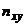раз. Поэтому данные наблюдений группируют, т. е. подсчитывают частоты 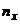, , 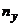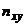. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.

Пример 2. Отыскание выборочного уравнения прямой линии регрессии по сгруппированным данным

По данным 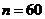наблюдений получена корреляционная таблица значений величин и . Найти выборочные уравнения прямых линий регрессии на и на . Построить эти прямые. Найти выборочный коэффициент корреляции. Оценить тесноту и обоснованность связи.

Y X
0,4
0,6
0,8

Решение. 1) Вычислим частоты наблюдаемых значений.

Y X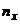
0,4
0,6
0,8

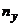Составим расчетную таблицу.

№

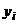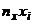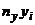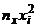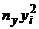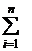Из расчетной таблицы получаем

2) Так как выборочный коэффициент корреляции не очень близок к 1, то линейная связь между признаками и не очень тесная; , следовательно, связь признаками и отрицательная. Вычислим , следовательно, наличие связи между признаками и у всей генеральной совокупности достаточно обоснованно (выборка репрезентативна).

3) Составим выборочные уравнения прямых линий регрессии на и на : Выборочное уравнение прямой линии регрессии на имеет вид:

или .

Выборочное уравнение прямой линии регрессии на имеет вид:

, или.