Вычисление доверительных интервалов

Пусть количественный признак Х генеральной совокупности распределён нормально. Будем рассматривать выборочную среднюю 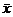как случайную величину 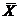( 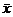изменяется от выборки к выборке); а выборочные значения признака 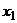, , 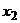…, , 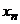как одинаково распределённые независимые случайные величины , , …, .

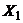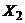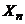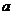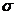Примем без доказательства, что если случайная величина Х распределена нормально с математическим ожиданием и СКО , то выборочная средняя 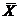, найденная по независимым наблюдениям, также распределена нормально с математическим ожиданием 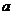и СКО, равным 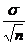. Потребуем, чтобы выполнялось соотношени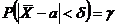е , где 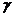– заданная надежность.

Допустим, что из некоторых соображений известно СКО 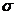исследуемого признака.

Пользуясь формулой для вычисления вероятности заданного отклонения нормально распределённой случайной величины 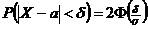, получим 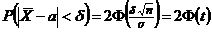, где 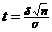. Отсюда .

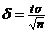Таким образом, доверительный интервал для оценки математического ожидания нормального распределения с известным СКО 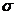: 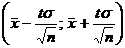,где 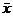– выборочная средняя, 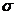– известное среднее квадратическое отклонение, 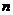– объем выборки, 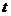– число, которое определяется из равенства 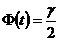по таблице функции Лапласа (Приложение 1), 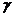– заданная надежность.

Замечание 1. Оценку 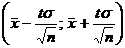называютклассической.Из формулы 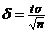, определяющей точность классической оценки можно сделать выводы:

1) при возрастании объёма выборки точность оценки увеличивается;

2) увеличение надёжности приводит к увеличению параметра 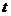, а следовательно, к возрастанию числа 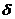, т.е. к уменьшению точности оценки.

Замечание 2. если требуется оценить математическое ожидание с наперёд заданной точностью 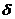и надёжностью 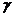, то минимальный объём выборки, который обеспечит эту точность, можно найти по формуле .

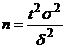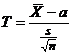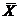В случае, когда значение СКО признака Х неизвестно, по данным выборки строят случайную величину , где – выборочная средняя, 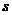– исправленное выборочное СКО, 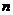– объём выборки, которая будет распределена по закону Стьюдента с 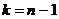степенями свободы. Тогда (см. [7]) можно доказать, что точность оценки 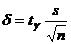, где 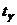– число, которое определяется по заданным 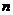и 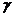по таблице распределения Стьюдента .

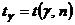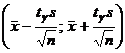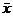Таким образом, доверительный интервал для оценки математического ожидания нормального распределения с неизвестным СКО: ,где – выборочная средняя, 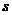– исправленное выборочное среднее квадратическое отклонение, 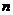– объем выборки, 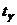– число, которое определяется по заданным 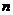и 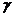по таблице распределения Стьюдента 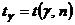(Приложение 2), 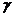– заданная надежность.

Замечание 1.Так как при неограниченном возрастании объёма выборки распределение Стьюдента стремится к нормальному, то при 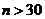вместо распределения Стьюдента можно пользоваться нормальным распределением. Для малых выборок замена распределения Стьюдента нормальным приводит к грубым ошибкам, а именно – к неоправданному сужению доверительного интервала.

Замечание 2. Достоинствами распределения Стьюдента является независимость от неизвестных параметров 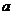и 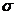, а зависимость только от объёма выборки .

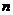Замечание 3. Использование распределения Стьюдента даёт более широкий доверительный интервал для оценки математического ожидания, чем использование нормального распределения. Этот факт объясняется тем, что малая выборка содержит мало информации об исследуемом признаке.

По найденному исправленному выборочному СКО 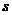можно с заданной надежностью 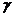найти доверительный интервал для оценки неизвестного СКО нормально распределённой случайной величины Х. Для этого потребуем, чтобы выполнялось соотношение 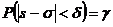. Тогда для оценки 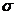получится неравенство 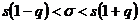, где 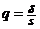. Значения параметра 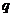можно найти с помощью распределения случайной величины 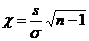(см. [7]) или специальных таблиц (Приложение 3).

Таким образом, доверительный интервал для оценки среднего квадратического отклонения нормального распределения: 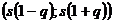,где 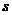– исправленное выборочное среднее квадратическое отклонение, 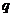– число, которое определяется по заданным 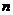и 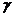по таблице распределения 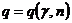(Приложение 3), 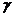– заданная надежность, 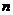– объем выборки.

Пример 2.4. Из генеральной совокупности значений нормально распределенного признака Х извлечена выборка объемом :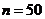

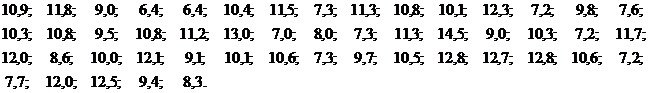
1) Найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения с надежностью 0,95.

2) Найти доверительный интервал для оценки математического ожидания с надежностью 0,95, если известно, что среднее квадратическое отклонение .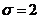

Решение. 1) Для построения интервального вариационного ряда воспользуемся решением примера 1.2:

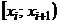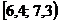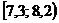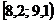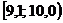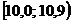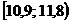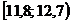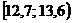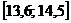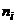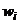	0,12	0,12	0,08	0,10	0,24	0,12	0,12	0,08	0,02
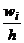	0,13	0,13	0,09	0,11	0,27	0,13	0,13	0,09	0,02

2) Найдём доверительные интервалы для вычисления оценки математического ожидания и среднего квадратического отклонения. Выборочная средняя (согласно примеру 2.2) равна:

Вычислим выборочную дисперсию:

Тогда исправленная выборочная дисперсия ,

а исправленное СКО .

Доверительный интервал для оценки математического ожидания нормального распределения с неизвестным СКО имеет вид: 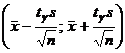. Найдём 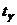по заданным объему выборки 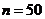и надежности 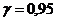по таблице распределения Стьюдента 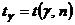(Приложение 3): 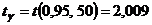. Тогда доверительный интервал примет вид: или .

Доверительный интервал для оценки среднего квадратического отклонения нормального распределения имеет вид: 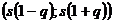. Найдём 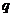по заданным объему выборки 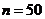и надежности 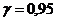по таблице распределения 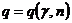(Приложение 4): 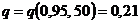. Тогда доверительный интервал примет вид:

Или .

3) Найдём доверительный интервал для оценки математического ожидания с надежностью 0,95, если известно, что среднее квадратическое отклонение 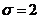. Доверительный интервал для оценки математического ожидания нормального распределения с известным СКО имеет вид: 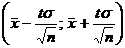. Найдём 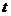из равенства 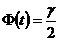по таблице функции Лапласа (Приложение 2) по заданной надежности 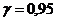. Тогда 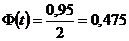и 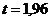. Вычислим концы доверительного интервала: или .

Таким образом, доверительный интервал для математического ожидания нормального распределения, вычисленный при известном СКО, уже, чем при неизвестном.

Практическое занятие.
Точечные и интервальные оценки генеральной совокупности

Задания для решения на практическом занятии

1. Выборка задана в виде распределения частот:

хi
ni

Найти распределение относительных частот. Построить полигон частот и эмпирическую функцию распределения.

2. Построить полигон частот и относительных частот по данному распределению выборки:

хi
ni

Найти выборочную среднюю, выборочную и исправленную дисперсии.

3. Задана выборка количественного признака непрерывной случайной величины Х. Найти ряд распределения частот и относительных частот. Построить гистограмму частот.

Выборка: 1; 2; 3; 1; 1.5; 4; 4.8; 2.5; 2; 5.6; 8; 8.2; 6; 6.3; 6.8; 7.; 5.8; 5; 5.2; 3.8; 5.3; 5.5; 4.5; 4.3; 4.6; 5.1; 9; 9.5; 10.

4. Из генеральной совокупности извлечена выборка объема :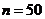

хi
ni

Найти несмещенную оценку генеральной средней.

5. По выборке объема n=41 найдена смещенная оценка D_в =3 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.

6. В таблице приведены результаты измерения роста (в см) случайно отобранных 100 студентов. Найти выборочную среднюю и выборочную дисперсию роста обследованных студентов.

Рост (см)	154-158	158-162	162-166	166-170	170-174	174-178	178-182
Число студентов

Указание. Найти середины интервала и принять их в качестве вариант.

7. Заданы генеральная совокупность и выборка некоторой дискретной случайной величины Х. Найти числовые характеристики генеральной совокупности и их точечные оценки. Построить полигон частот (теоретических и эмпирических). Составить теоретическую и эмпирическую функции распределения, построить их графики.

Генеральная совокупность. 1, 1, 2, 5, 5, 3, 5, 8, 5, 1, 4, 6, 2, 3, 7, 4, 7 ,5, 2, 3, 5, 4, 2, 1, 1, 8, 9, 7, 10, 5, 5, 6, 4, 4, 2, 1, 10, 7, 5, 8, 4, 7, 3, 3, 4, 6, 8, 7, 8, 4, 2, 7, 6, 7, 8, 6, 8, 5, 4, 2, 1, 10, 10, 2, 10, 5, 6, 5, 4, 4, 5, 5, 5, 6, 9, 8, 5, 4, 4, 5, 6 ,8, 5, 2, 1, 1, 3, 5, 4, 5, 8, 7, 3, 3, 5, 6, 6, 5, 4, 4.

Выборка. 1,3,3,5,4,8,9,5,10,5,6,4,7,5,8,6,4,1,2,3.

8. Пусть признак Х – оценка за контрольную работу по математике в вашей группе. Найти закон распределения случайной величины, построить полигон распределения, функцию распределения, найти числовые характеристики случайной величины.

9. Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания a нормально распределенного признака Х генеральной совокупности, если генеральное СКО s = 5, выборочная средняя 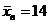, объем выборки n=25.

10. Станок-автомат штампует валики. По выборке объема n = 100 вычислена выборочная средняя диаметров изготовленных валиков. Найти с надежностью 0,95 точность, с которой выборочная средняя оценивает математическое ожидание диаметров изготовляемых валиков, зная, что их СКО s = 2 мм. Предполагается, что диаметры валиков распределены нормально.

11. Найти минимальный объем выборки, при котором с надежностью 0,975 точность оценки математического ожидания а генеральной совокупности по выборочной средней равна d = 0,3, если известно СКО s = 1,2 нормально распределенной генеральной совокупности.

12. Из генеральной совокупности извлечена выборка объема n=10:

xi	-2
ni

а) Оценить с надежностью 0,95 при помощи доверительных интервалов математическое ожидание нормально распределенного признака генеральной совокупности; генеральное СКО, если известна дисперсия D=2,5.

б) Оценить с надежностью 0,95 при помощи доверительных интервалов математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней, если дисперсия неизвестна.

Сравнить полученные результаты.

в) Оценить с надежностью 0,95 при помощи доверительных интервалов генеральное СКО по исправленному СКО,

13. По данным объема выборки n=16 из генеральной совокупности найдено исправленное СКО s=1 нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное СКО s с надежностью 0,95.

14. По данным девяти равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений 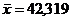и исправленное СКО s=5. Оценить истинное значение измеряемой величины с надежностью 0,95.

Задания для самостоятельной работы

1. Выборка задана в виде распределения частот:

хi
ni

Найти распределение относительных частот, построить полигон и эмпирическую функцию распределения.

2. Построить полигон частот по данному распределению выборки. Построить полигон относительных частот. Составить и построить эмпирическую функцию распределения.

хi
ni

3. Из генеральной совокупности извлечена выборка объема n=50:

хi	18,4	18,9	19,3	19,6
ni

Найти выборочную дисперсию и исправленную выборочную дисперсию.

4. По выборке объема n=51 найдена смещенная оценка D_в =5 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.

5. Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 часов. Найти с надежностью 0,95 доверительный интервал средней продолжительности а горения лампы всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы s = 40 часов. Предполагается, что продолжительность горения ламп распределена нормально.

6. Из генеральной совокупности извлечена выборка объема n=12:

xi	-0,5	-0,4	-0,2		0,2	0,6	0,8		1,2	1,5
ni

Оценить с надежностью 0,95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала. .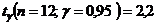

7. По данным объема выборки n=10 из генеральной совокупности найдено исправленное СКО s=5,1 нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное СКО s с надежностью 0,999.

8. Количественный признак Х генеральной совокупности распределен нормально. По выборке объема n=16 найдены выборочная средняя 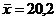и исправленное СКО s=0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

9. Найти минимальный объем выборки, при котором с надежностью 0,95 точность оценки математического ожидания а генеральной совокупности по выборочной средней равна d = 0,2, если известно СКО s = 1,5 нормально распределенной генеральной совокупности.