Алгоритм построения гистограммы

1) Определить длину промежутка 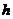. Для этого сначала нужно найти разницу 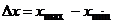, из практических соображений определить число промежутков 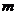, тогда .

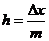2) Вычислить значения концов промежутков. Первый способ. За значение левого конца первого промежутка принимают 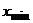, все остальные концы промежутков получаются по формуле 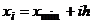, 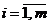(все промежутки, кроме последнего, имеют вид: 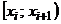, последний промежуток имеет вид 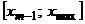). Второй способ. За значение левого конца первого промежутка принимают 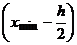, за правый – 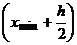. Все остальные значения концов промежутков получаются по формуле 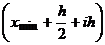, 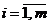(в этом случае промежутков получится 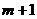больше, все промежутки имеют вид: ).

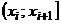3) Вычислить сумму частот (относительных частот) наблюдаемых значений, попавших в каждый из интервалов.

4) Построить прямоугольники, основаниями которых служат частичные интервалы длиной 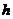, а высоты равны отношению 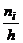(соответственно ).

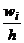Пример 1.1. Распределение рабочих механического цеха по тарифному разряду имеет вид:

Тарифный разряд							сумма
Количество рабочих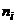

Построить полигон частот, полигон относительных частот, кумуляту и эмпирическую функцию распределения.

Решение.1)Для построения полигона частот требуется нанести на плоскость 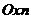координаты точек .

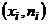2) Для полигона относительных частот требуется найти распределение относительных частот и нанести на плоскость 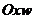координаты точек .

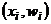2) Для построения кумуляты требуется найти значения накопленных частот.

3) Для построения эмпирической функции распределения требуется найти распределение относительных частот и значения накопленных относительных частот.

Результаты вычислений сведём в таблицу:

Тарифный разряд							сумма
Количество рабочих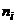
Относительные частоты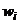
Накопленные частоты: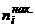
Накопленные относительные частоты: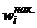

Пример 1.2. Из генеральной совокупности значений нормально распределенного признака Х извлечена выборка объемом :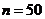

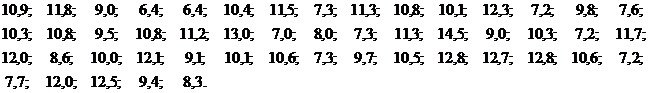
Построить гистограмму и кумуляту относительных частот, и эмпирическую функцию распределения

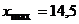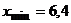Решение. 1) Построим гистограмму относительных частот. По выборке определяем, что , а тогда 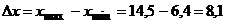. Целесообразно взять число интервалов 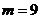, тогда 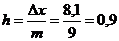. За значение левого конца первого промежутка примем 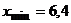, за правый – 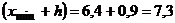. Все остальные значения концов промежутков получаются по формуле , .

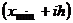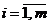Вычислим сумму частот, а затем и относительных частот вариант, попавших в каждый из промежутков.

Результаты вычислений запишем в таблицу.

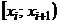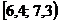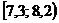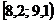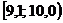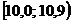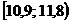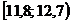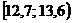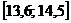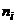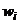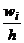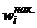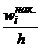Построим прямоугольники, основаниями которых служат частичные интервалы длиной 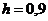, а высоты равны отношению .

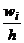2) Для построения кумуляты и эмпирической функции распределения найдём величины накопленных частот 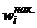и величины 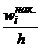. Построим соответствующие графики:

Замечание. Для дискретного вариационного ряда

Для интервального вариационного ряда

Статистические оценки параметров распределения