Теоремы сложения и умножения вероятностей и следствия из них

[3. Ч.1, гл.2 - 4 полностью, гл.5, § 1].

Пример 1. Два охотника стреляют по одной мишени и имеют вероятности попадания 0,7 и 0,8 соответственно. Оба сделали по одному выстрелу. Какова вероятность того, что

а) в мишени ровно две пробоины,

б) в мишени хотя бы одна пробоина,

в) в мишени ровно одна пробоина?

Решение. Введем обозначения: событие А - попал первый охотник, 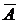- первый охотник промахнулся, В - попал второй охотник, 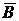- второй охотник промахнулся, С - в мишени ровно две пробоины, D - в мишени хотя бы одна пробоина, Е - в мишени ровно одна пробоина.

Событие С состоит в том, что произошло и А, и В одновременно, то есть произошло произведение событий АВ , т.е. С = АВ. Событие D состоит в том, что произошло хотя бы одно из событий А или В, то есть сумма событий А + В , т.е. D = А + В, и, наконец, событие Е состоит в том, что А произошло а В нет или В произошло а А нет, Е = A 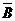+ 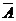B. Учитывая, что А и В независимые события (вероятность попадания одного из охотников не зависит от того попал другой или нет)

Р ( 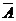) = 1 - Р(А) = 0,3 и Р ( 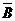) = 1 - Р(В) = 0,2.

Следовательно

Р(С) = 0,7´0,8 = 0,56 ,

Р(D) = Р(А) + Р(В) - Р(АВ) = 0,7 + 0,8 - 0,7х0,8 = 0,94 ,

Р(Е) = Р(А)Р( 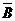) + Р( 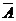)Р(В) = 0,7х0,2 + 0,3х0,8 = 0,38.

Пример 2. На фабрике, изготовляющей болты, первая машина производит 25 %, а вторая – 35 %, третья – 40 % всех изделий. В их продукции брак составляет соответственно 5, 4 и 2 %.

а) Какова вероятность того, что случайно выбранный болт дефектный?

в) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой машиной?

Решение. а) Обозначим за Н₁ событие – болт сделан на первой машине, за Н₂ событие – болт сделан на второй машине, за Н₃ событие – болт сделан на третьей машине. Тогда: Р(Н₁) = 0,25 – вероятность того, что болт сделан на первой машине. Соответственно Р(Н₂) = 0,35 и Р(Н₃) = 0,40.

Пусть событие А – болт бракован, тогда Р (А|Н₁) = 0,05 – вероятность, что брак выпущен первой машиной, соответственно Р(А|Н₂) = 0,04, а Р(А|Н₃) = 0,02.

Р(А) = Р(Н₁)·Р(А|Н₁) + Р(Н₂)·Р(А|Н₂) + Р(Н₃)·Р(А|Н₃) = 0,25 · 0,05 + 0,35 · 0,04 + 0,40 · 0,02 + 0,0125 + 0,014 + 0,008 = 0,0345.

Б) Р(Н₁|А) – вероятность того, что дефектный болт произведен первой машиной

.

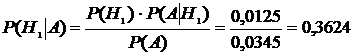Пример 3. Что вероятнее выиграть у равносильного противника: а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми, если ничьих не бывает?

Решение. Для равносильных противников вероятность выигрыша (проигрыша) одинакова, то есть .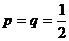

а) Вероятность выигрыша m партий из n 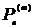задается формулой

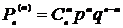
В первом случае n=4, m=3. Следовательно, вероятность выиграть три партии из четырех

.

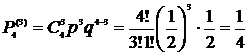Когда n=8, а m=5, то

.

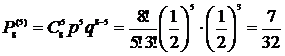Следовательно, .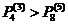

Б) Вероятность выиграть не менее трех партий есть сумма вероятностей выиграть три или четыре партии из четырех, так как эти события несовместны, то

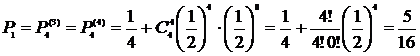
(Напомним, что 0!=1).

Аналогично, вероятность выиграть не менее пяти партий из восьми

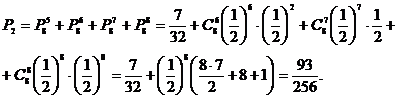
Р_{2 >} Р_1.

Следовательно, выиграть не менее пяти партий из восьми вероятнее.

Контрольная работа № 4. Задания.

1. Определить область сходимости ряда:

1.1.	1.11.
1.2.	1.12.
1.3.	1.13.
1.4.	1.14.
1.5.	1.15.
1.6.	1.16.
1.7.	1.17.
1.8.	1.18.
1.9.	1.19.
1.10.	1.20.