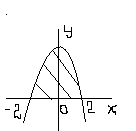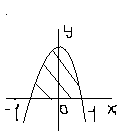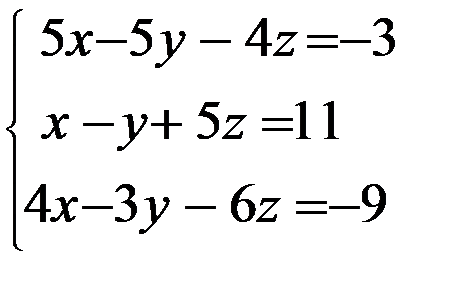Для специальностей технического профиля
МАТЕМАТИКА
Методические указания
для студентов заочной формы обучения
Для специальностей технического профиля
Челябинск, 2017
Содержание
Введение. 3
Методические указания к контрольной работе. 3
Методические рекомендации по изучению теоретического материала и выполнению практических работ. 16
ЛИТЕРАТУРА.. 61
Введение
Методические указания для студентов заочной формы обучения по учебной дисциплине «Математика» предназначены для реализации Федерального государственного образовательного стандарта для специальностей технического профиля.
Самостоятельная работа при заочной форме обучения является основным видом учебной деятельности и предполагает следующее:
− самостоятельное изучение теоретического материала;
− подготовку к зачету.
Настоящие методические указания составлены в соответствии с рабочей программой учебной дисциплины, утвержденной в многопрофильном колледже.
Цель методических указаний - помочь студентам при самостоятельном освоении программного материала и выполнении домашней контрольной работы.
Методические указания включают:
1. Паспорт рабочей программы учебной дисциплины.
2. Методические рекомендации по выполнению контрольной работы.
3. Методические рекомендации к практическим работам.
4. Задания для дифференцированного зачета.
5. Информационное обеспечение.
Наряду с настоящими методическими указаниями студенты заочной формы обучения должны использовать учебно-методический комплекс учебной дисциплины, включающий рабочую программу; методические указания для самостоятельной работы; методические указания для практических занятий; практикум; учебное пособие.
Рабочим учебным планом для студентов заочной формы обучения предусматриваются теоретические и практические занятия. Обзорные лекции проводятся по сложным для самостоятельного изучения темам программы и должны помочь студентам систематизировать результаты самостоятельных занятий.
По итогам изучения дисциплины проводится дифференцированный зачет.
Методические указания к контрольной работе
ПРАВИЛО ВЫБОРА ВАРИАНТА
Вариант контрольной работы определяется в зависимости от порядкового номера студента в учебном журнале. При необходимости можете уточнить Ваш вариант у заведующей отделением.
Контрольная работа содержит 12 заданий по темам «Дифференциальное исчисление», «Интегральное исчисление», «Комплексные числа», «Элементы линейной алгебры», «Теория вероятностей и математическая статистика». В каждом задании по 20 вариантов.
Будьте внимательны при выборе варианта. Работа, выполненная не по своему варианту, возвращается без проверки.
Тема 1 «Дифференциальное исчисление»
Задание 1. Вычислить производную функции:
1. 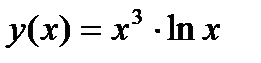 2. 2. 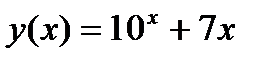 3. 3. 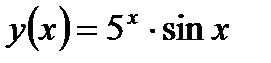 4. 4. 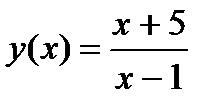 5. 5. 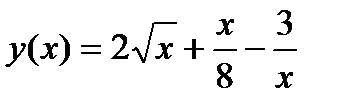 6. 6. 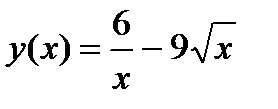 7. 7. 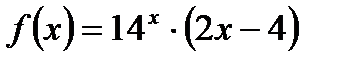 8. 8. 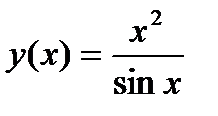 9. 9. 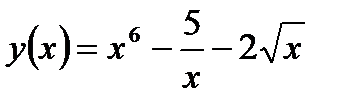 10. 10. 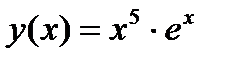 | 11. 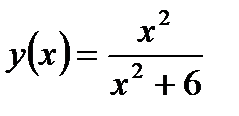 12. 12. 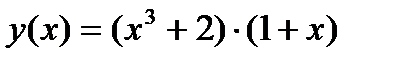 13. 13. 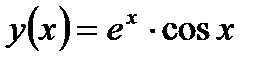 14. 14. 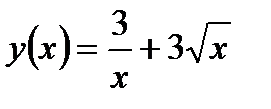 15. 15. 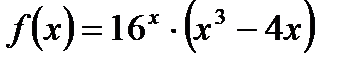 16. 16. 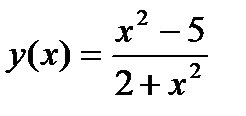 17. 17. 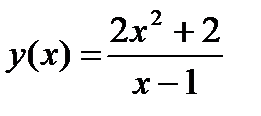 18. 18. 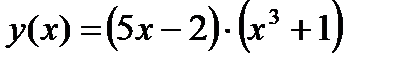 19. 19. 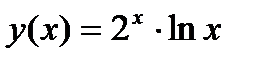 20. 20. 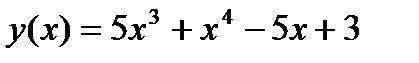 |
Задание 2. Вычислить производную сложной функции:
1. 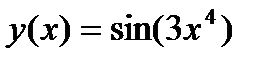 2. 2. 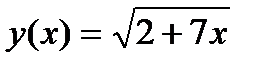 3. 3. 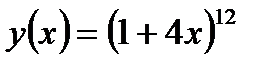 4. 4. 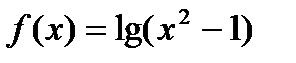 5. 5. 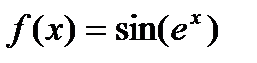 6. 6. 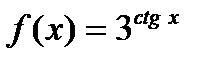 7. 7. 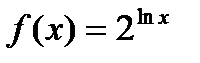 8. 8. 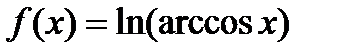 9. 9. 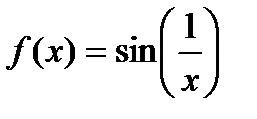 10. 10. 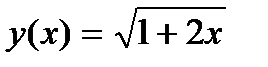 | 11. 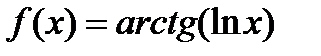 12. 12. 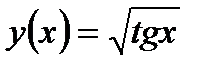 13. 13. 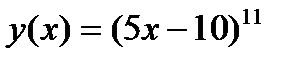 14. 14. 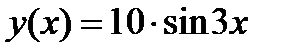 15. 15. 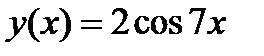 16. 16. 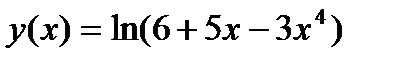 17. 17. 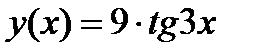 18. 18. 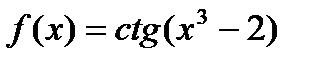 19. 19. 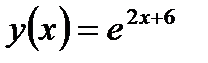 20. 20. 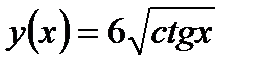 |
Задание 3. Решить задачу с применением производной:
1. Тело движется прямолинейно по закону 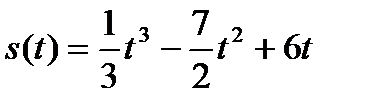 (м). Вычислить скорость и ускорение в момент времени 2 сек.
(м). Вычислить скорость и ускорение в момент времени 2 сек.
2. Тело движется прямолинейно по закону 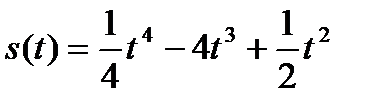 (м) . В какой момент времени ускорение равно нулю?
(м) . В какой момент времени ускорение равно нулю?
3. Тело, брошенное вертикально вверх движется по закону: 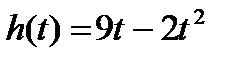 (м). Найти наибольшую высоту подъема.
(м). Найти наибольшую высоту подъема.
4. Движение тела происходит по закону 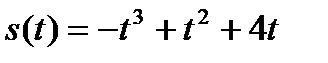 (м).Определить скорость и ускорение в момент времени 5 сек.
(м).Определить скорость и ускорение в момент времени 5 сек.
5.Тело массой 2 кг. движется прямолинейно по закону 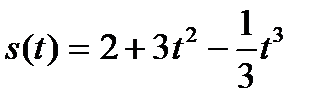 . Определить силу, действующую на тело в момент времени
. Определить силу, действующую на тело в момент времени 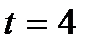 с
с
6.Тело движется прямолинейно по закону 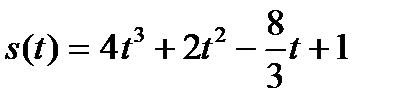 (м). Определить скорость и ускорение в момент времени
(м). Определить скорость и ускорение в момент времени 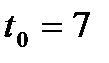 .
.
7.Тело массой 2 кг. движется прямолинейно по закону 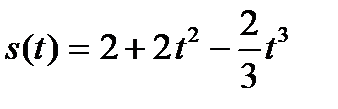 . Определить кинетическую энергию тела в момент времени
. Определить кинетическую энергию тела в момент времени 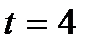 с.
с.
8.Тело, брошенное вертикально вверх, движется по закону 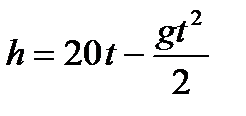 (м), где g=9,8. Найти скорость тела через 3 с после начала движения. В какой момент времени тело достигнет наивысшей высоты?
(м), где g=9,8. Найти скорость тела через 3 с после начала движения. В какой момент времени тело достигнет наивысшей высоты?
9.Тело массой 3 кг. движется прямолинейно по закону 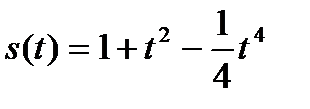 . Определить силу, действующую на тело в момент времени
. Определить силу, действующую на тело в момент времени 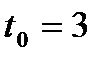 с.
с.
10.Тело движется по закону 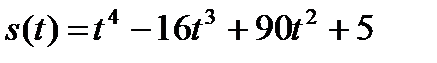 (м). Найти ускорение в момент времени
(м). Найти ускорение в момент времени 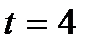 с.
с.
11. Тело движется по закону 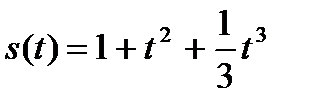 (м). Определить силу, действующую на тело в момент времени 2 сек, если масса тела 8 кг.
(м). Определить силу, действующую на тело в момент времени 2 сек, если масса тела 8 кг.
12. Тело массой 2 кг. движется прямолинейно по закону 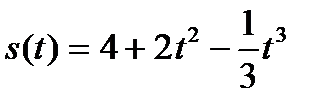 . Определить кинетическую энергию тела в момент времени
. Определить кинетическую энергию тела в момент времени 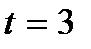 с.
с.
13. Тело, брошенное вертикально вверх, движется по закону 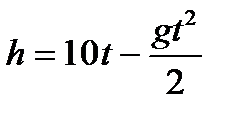 (м), где g=9,8.Найти скорость тела через 2с после начала движения.
(м), где g=9,8.Найти скорость тела через 2с после начала движения.
14. Тело движется прямолинейно по закону 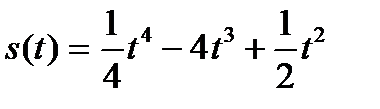 (м). В какой момент времени ускорение равно нулю?
(м). В какой момент времени ускорение равно нулю?
15. Тело движется прямолинейно по закону 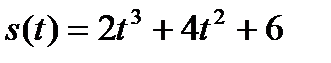 (м.) Найти кинетическую энергию в момент времени 2 сек., если масса тела 10 кг.
(м.) Найти кинетическую энергию в момент времени 2 сек., если масса тела 10 кг.
16. Тело, брошенное вертикально вверх движется по закону: 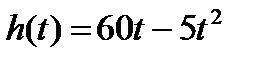 (м). Найти момент времени, когда тело достигнет наибольшей высоты.
(м). Найти момент времени, когда тело достигнет наибольшей высоты.
17. Тело движется прямолинейно по закону 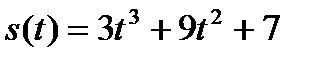 (м.) Найти кинетическую энергию в момент времени 1 сек, если масса тела 8 кг.
(м.) Найти кинетическую энергию в момент времени 1 сек, если масса тела 8 кг.
18.Тело движется по закону 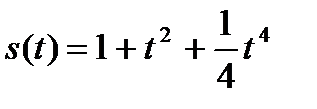 (м). Определить силу, действующую на тело в момент времени 3сек., если масса тела 6 кг.
(м). Определить силу, действующую на тело в момент времени 3сек., если масса тела 6 кг.
19. Тело, брошенное вертикально вверх движется по закону: 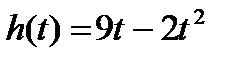 (м). Найти ускорение тела и наибольшую высоту подъема.
(м). Найти ускорение тела и наибольшую высоту подъема.
20.Тело движется прямолинейно по закону 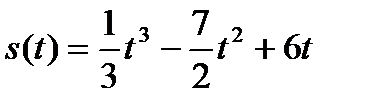 (м). Вычислить скорость и ускорение в момент времени 2 сек.
(м). Вычислить скорость и ускорение в момент времени 2 сек.
Тема 2 «Интегральное исчисление»
Задание 4. Вычислить неопределенный интеграл:
1. 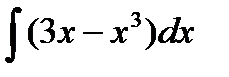 2. 2. 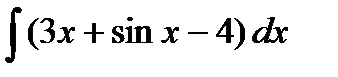 3. 3. 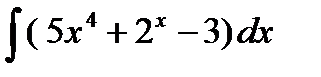 4. 4. 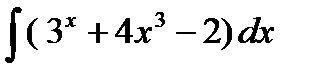 5. 5. 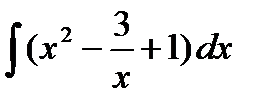 6. 6. 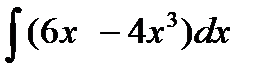 | 11. 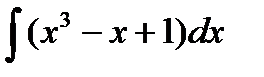 12. 12. 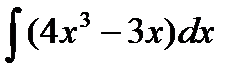 13. 13. 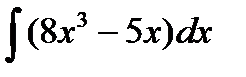 14. 14. 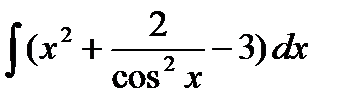 15. 15. 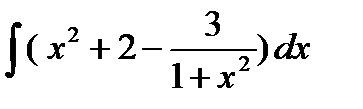 |
7. 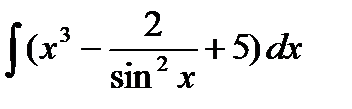 8. 8. 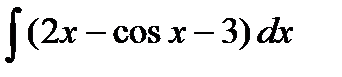 9. 9. 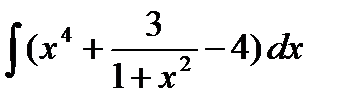 10. 10. 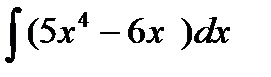 | 16. 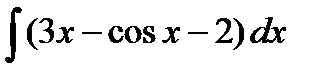 17. 17. 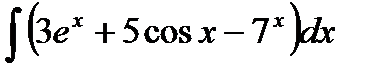 18. 18. 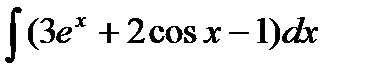 19. 19. 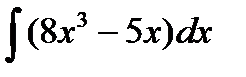 20. 20. 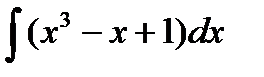 |
Задание 5. Вычислить неопределенный интеграл способом замены переменной:
1. 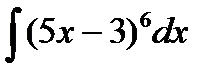 2. 2. 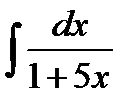 3. 3. 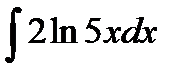 4. 4. 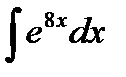 5. 5. 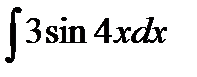 6. 6. 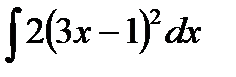 7. 7. 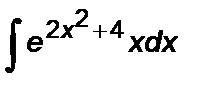 8. 8. 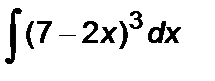 9. 9. 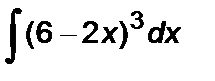 10. 10. 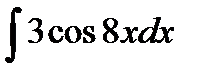 | 11. 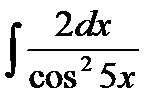 12. 12. 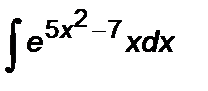 13. 13. 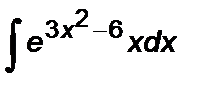 14. 14. 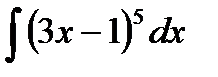 15. 15. 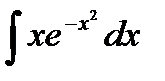 16. 16. 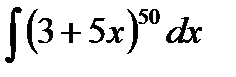 17. 17. 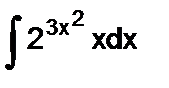 18. 18. 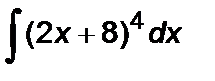 19. 19. 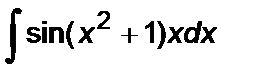 20. 20. 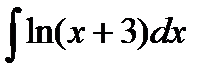 |
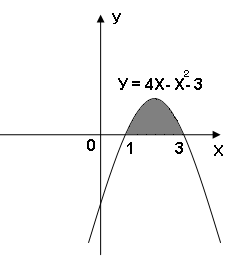
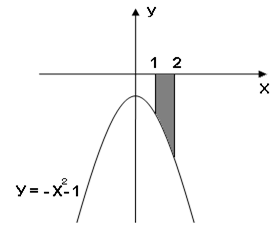
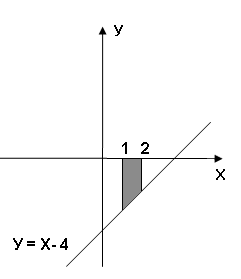
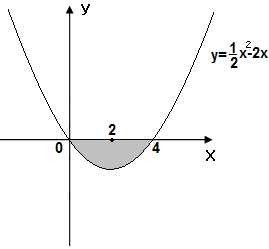
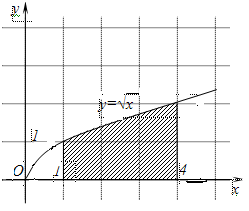
Задание 6. Вычислить площадь выделенной фигуры с помощью определенного интеграла.
1.
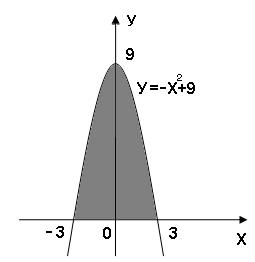
2.
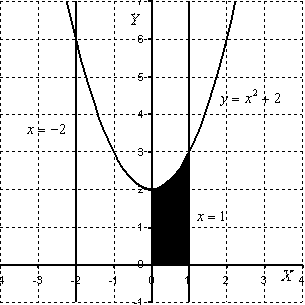
3.
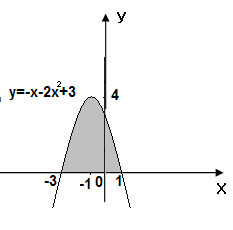
5.
6.
7.
8.
9.
10.
| 11. 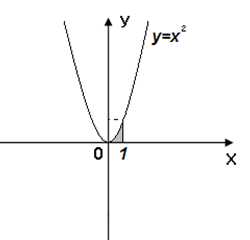 12. 12. 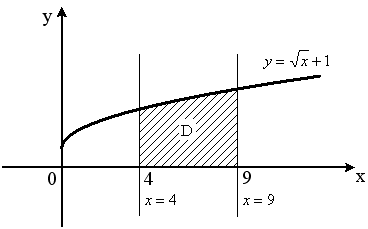 13. 13. 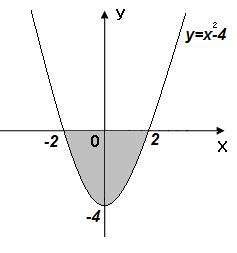 14. 14. 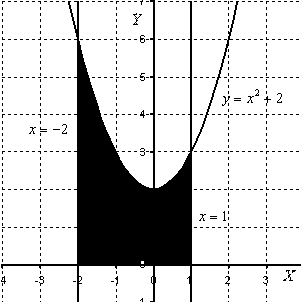 15. 15. 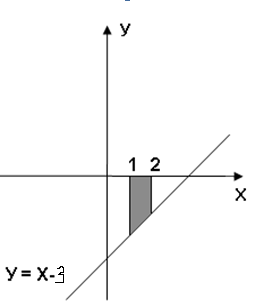 16. 16. 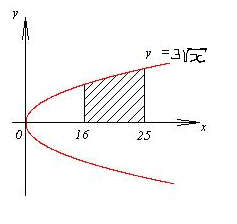 17. 17. 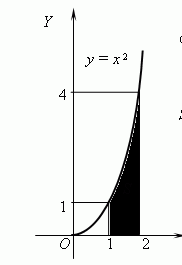 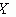 18. 18. 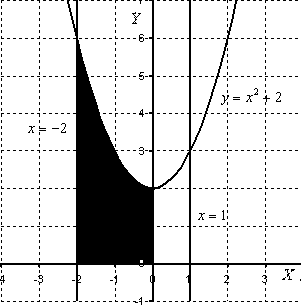 19. 19. 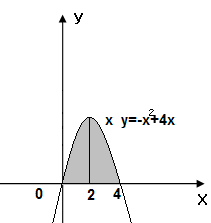 20. 20. 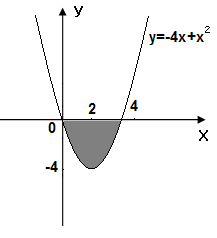 |
Тема 3. «Теория вероятностей и математическая статистика»
Задание 7. Решить задачу:
1. В магазине работают 2 мужчин и 7 женщин. Трое из них должны пойти в отпуск летом. Кто именно – определяется жребием. Найти вероятность того, что летом в отпуск пойдут только женщины.
2. В пачке 10 тетрадей, среди них 4 тетради в клетку, а остальные в линейку. Найти вероятность того, что среди наудачу взятых трех тетрадей все в клетку.
3. В ящике лежат 3 красных, 5 синих и 10 белых шаров. Какова вероятность, что вынутый шар красный?
4. Из 20 методичек по математике 3 по теории вероятностей. Студент наудачу взял две методички.
Найти вероятность того, что среди взятых нет методичек по теории вероятностей.
5. Среди 10 документов, поступивших в офис, два оформлены с ошибками. Для проверки наудачу взяли 4 документа. Какова вероятность того, что среди них нет неверно оформленных документов?
6. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность выиграть, купив 1 билет?
7. Среди 15 счетов 3 счета оформлены неверно. Ревизор наудачу берет 2 счета. Найти вероятность того, что среди взятых счетов все оформлены неверно.
8. Из трех бухгалтеров, восьми менеджеров и шести научных работников необходимо сформировать комитет из 3 человек. Найти вероятность того, что в комитете окажутся одни бухгалтера.
9. В урне лежат 5 красных, 7 синих и 11 белых шаров. Какова вероятность, что вынутый шар окажется белым?
10. Из 25 билетов ( пронумерованных от 1 до 25) выбирается 4. Какова вероятность того. что номер билета есть число, кратное 3?
11. Из 10 конструкций 3 высокого качества. Найти вероятность того, что среди взятых 2 конструкций высокого качества?
12. Учебная группа, состоящая из 15 юношей и 10 девушек, выбирает дежурных из 4 человек. Найти вероятность того, что в числе выбранных будут только юноши.
13. Студент знает 20 из 30 вопросов на экзамене. Найти вероятность того, что студент знает 2 вопроса, заданных ему.
14. Из 20 билетов ( пронумерованных от 1 до 20) выбирается 3. Какова вероятность того ,что номер билета есть число, кратное 4?
15. Из слова «автоматика» выбирается наугад буква. Какова вероятность того, что это буква «а»?
16. В партии, состоящей из 10 одинаково упакованных изделий, смешаны изделия двух сортов, причем 6 из этих изделий – первого сорта, а остальные изделия – второго сорта. Найти вероятность того, что взятые наугад два изделия окажутся 1-го сорта.
17. Из слова «математика» выбирается наугад буква. Какова вероятность того, что это буква «т»?
18. Бросают игральный кубик. Найдите вероятность того, что выпадет чётное число очков.
19. В коробке лежат 5 красных, 7 зелёных и 2 синих кубика. Случайным образом из коробки берут кубик. Какова вероятность того, что из коробки взяли зелёный кубик?
20. Участники жеребьёвки тянут из ящика жетоны с номерами от 1 до 100. Найдите вероятность того, что номер первого наудачу извлечённого жетона не содержит цифры 5.
Задание 8.
1-5. Ученики 9-го класса получили следующие четвертные оценки по математике: 4, 5, 5, 3, 4, 4, 4, 3, 5, 4, 5,5, 5, 3, 3, 4, 4, 4, 4, 3. Определите среднюю оценку, полученную учениками. Проверьте выполнение закона 3-х сигм.
6-10. Для оценки количества детей дошкольного возраста исследуют двадцать квартир. При опросе в каждой квартире оказалось детей указанного возраста следующее количество: 0; 1; 3; 1; 0; 4; 1; 2; 0; 0; 1; 2; 1; 0; 1; 0; 2; 0; 3; 1. Определите среднее количество детей дошкольного возраста. Проверьте выполнение закона 3-х сигм.
11-15. При обследовании потока пассажиров на автобусном маршруте из шести остановок на конечном пункте было опрошено 20 человек. Каждый называл номер остановки, на которой он вошел: 4; 1; 5; 4; 3; 1; 2; 5; 6; 5; 5; 3; 4; 4; 4; 5; 6; 5; 3; 4. Определите среднее значение номера остановки. Проверьте выполнение закона 3-х сигм.
16-20. Исследуется возраст студентов по 20 случайно выбранным личным делам. Получен результат: 16, 19, 18, 16, 16, 17, 19, 17, 19, 16, 17, 18, 17, 18, 17, 19, 16, 16, 18, 17. Определите средний возраст студентов. Проверьте выполнение закона 3-х сигм.
Тема 4 «Комплексные числа»
Задание 9. Даны комплексные числа в алгебраической форме. Выполнить указанные действия:
| 1. Z1= 2+3ί Z1+ Z2 ; Z1/ Z2 Z2= -4+4ί 2. Z1= 2-3ί Z1+ Z2 ; Z1/ Z2 Z2= 4+4ί 3. Z1= -2+3ί Z1+ Z2 ; Z1/ Z2 Z2= -4-4ί 4. Z1= -2-3ί Z1+ Z2 ; Z1/ Z2 Z2= 4-4ί 5. Z1= 2+3ί Z1+ Z2 ; Z1/ Z2 Z2= 4-4ί 6. Z1= 2+3ί Z1+ Z2 ; Z1/ Z2 Z2= -4-4ί 7. Z1= 2-3ί Z1+ Z2 ; Z1/ Z2 Z2= -4+4ί 8. Z1= 2-3ί Z1+ Z2 ; Z1/ Z2 Z2= -4-4i 9. Z1= -2+3i Z1+ Z2 ; Z1/ Z2 Z2= 4+4ί 10. Z1= -2-3i Z1+ Z2 ; Z1/ Z2 Z2= 4+4i | 11. 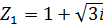 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 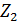 = = 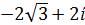 12. 12. 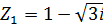 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 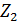 = = 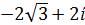 13. 13. 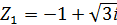 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 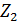 = = 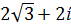 14. 14. 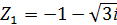 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 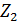 = = 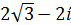 15. 15. 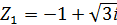 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 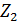 = = 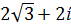 16. 16. 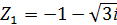 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 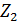 = = 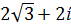 17. 17. 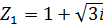 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 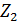 = = 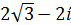 18. 18. 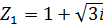 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 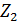 = = 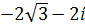 19. 19. 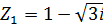 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 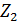 = = 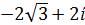 20. 20. 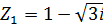 Z1- Z2 ; Z1×Z2 Z1- Z2 ; Z1×Z2 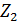 = = 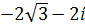 |
Задание 10. Перевести комплексные числа Z1 и Z2 тригонометрическую форму.
Тема 5 «Элементы линейной алгебры»
Задание 11. Даны матрицы:
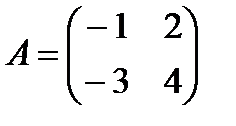
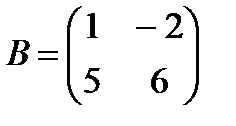
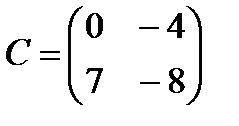
Выполните указанные действия с матрицами
| 1.ABТ -3C; 2.2AТ +BC; 3.AТB-2C; 4.3AB+CТ; 5.3ABТ -C; 6.2ABТ +C; 7.3AТ -BC; 8.AТ +2BC; 9.ACТ+3В; 10.2ACТ-В; | 11.2AТ C+В; 12.3A+CТB; 13.2A-BТC; 14.3CA-BТ; 15.2BТ+AC; 16.CB+3AТ; 17.CТ-2BA; 18.3BТ+СA; 19.2CТ-AB; 20.BA+CТ. |
Задание 12. Решить систему уравнений методом Крамера
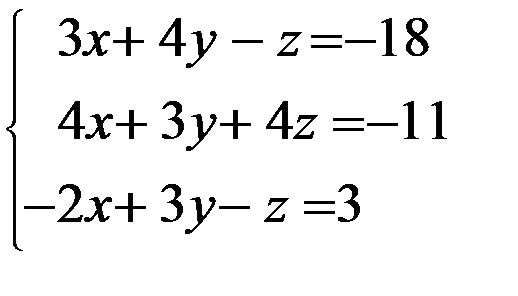 3. 3. 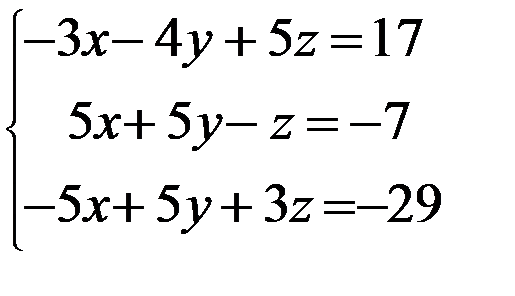 4. 4. 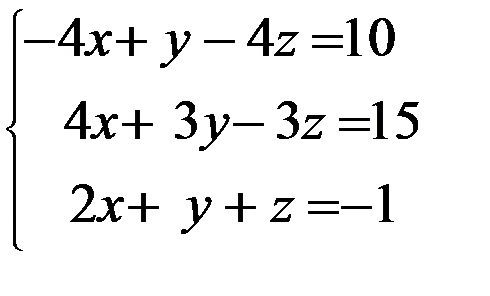 5. 5. 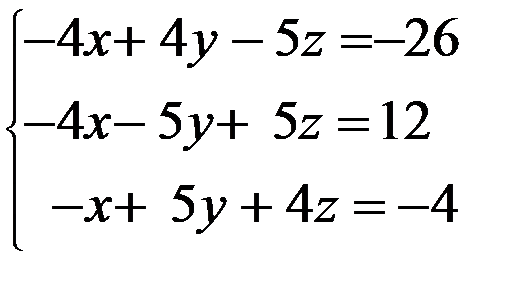 6. 6. 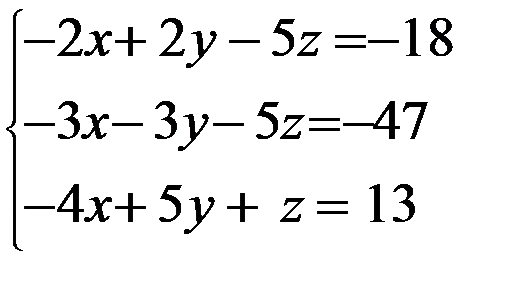 7. 7. 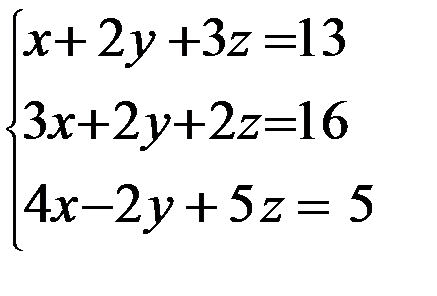 8. 8. 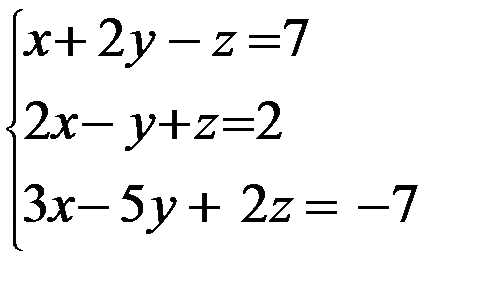 9. 9. 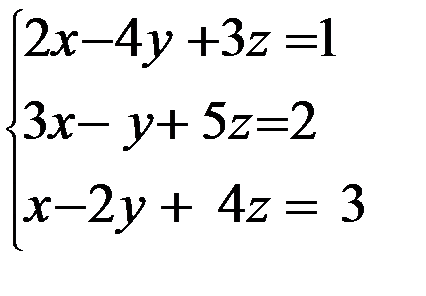 10. 10. 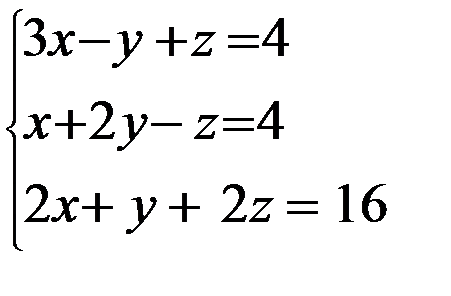 | 11. 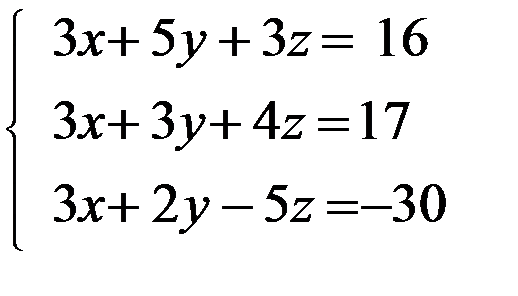 12. 12. 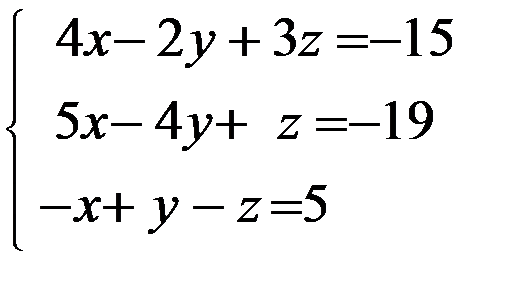 13. 13. 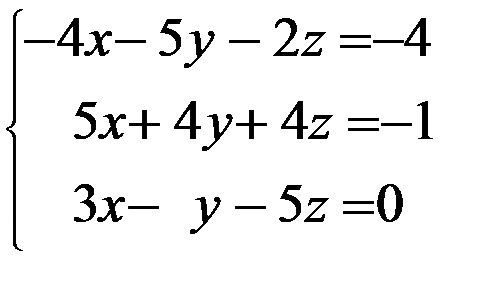 14. 14. 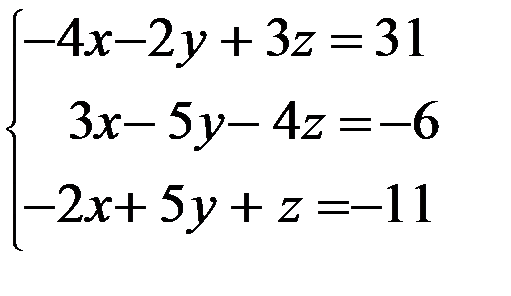 15. 15. 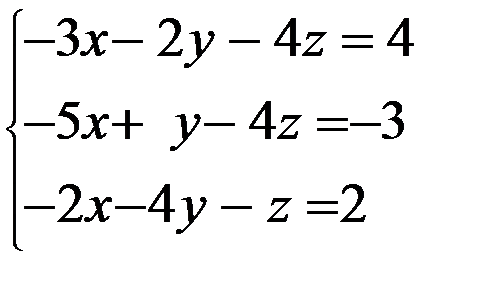 16. 16. 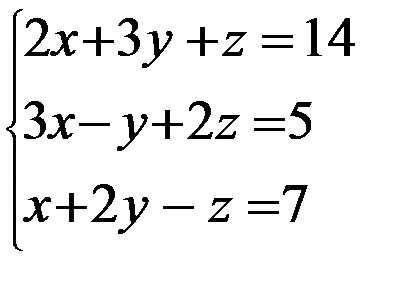 17. 17. 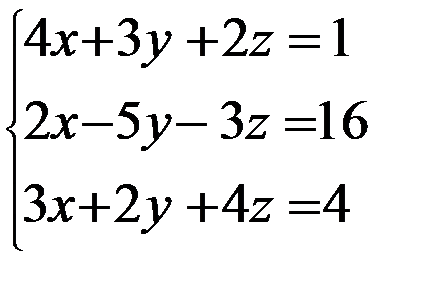 18. 18. 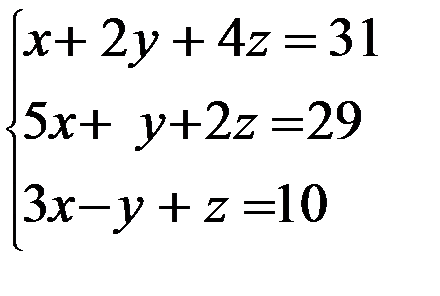 19. 19. 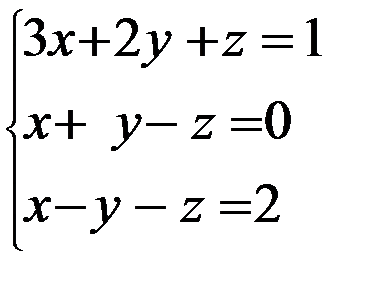 20. 20. 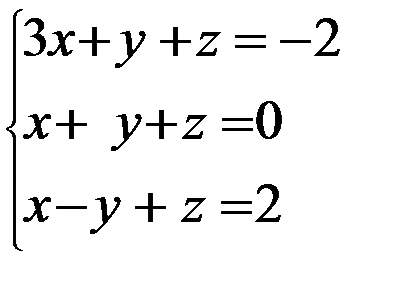 |
ПРАВИЛА ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
При выполнении контрольных работ по математике нужно придерживаться следующих правил:
1. Контрольную работу выполнять в тетради чернилами черного или синего цвета, оставляя поля для замечаний преподавателя.
2. На обложке тетради разборчиво написать фамилию, инициалы, номер варианта, название дисциплины «Математика». В конце работы указать дату выполнения и расписаться.
3. Работа обязательно должна содержать все задачи именно вашего варианта.
4. Решения задач располагать в порядке номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи записать полностью ее условие.
6. Решения задач излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. По результатам контрольной работы выставляется оценка.
8. Если контрольная работа возвращена на доработку, то необходимо исправить недочеты (в той же тетради) и сдать работу на повторную проверку.
9. Студенту, не выполнившему контрольную работу до начала экзаменационной сессии, может быть предложена аудиторная контрольная работа.
Методические рекомендации по изучению теоретического материала и выполнению практических работ
Приращение функции
Определение 1.Приращением величины называется разность между новым значением величины и старыми обозначается буквойΔ.
ΔN = N2 – N1.
Другими словами, приращение величины показывает на сколько изменилась величина.
Определение 2. Приращением аргумента (функции) называется разность между новым значением аргумента (функции) и старым и обозначается буквой Δ.
Δх = х2 – х1 - приращение аргумента;
Δу = у2 – у1 - приращение функции.
Если известны начальное значение величины N и ее ΔN, то можно найти ее новое (наращенное) значение N2 = N + ΔN.
Примеры
1. Найти приращение функции у=2х2 – 1, если х изменился от 3 ед. до 3,5 ед.
Решение
Найдем значение функции у1 при х1=3: у1=2∙32 – 1=17 ед,
затем найдем у2 при х2 = 3,5: у2 = 2∙3,52 – 1 = 23,5 ед.
Тогда Δу = у2 – у1 = 23,5 – 17 = 6,5 ед.
Производная функции
ОпределениеПроизводной функции называется предел отношения приращения функции Δy к приращению аргумента Δx, когда приращение аргумента стремится к нулю, и обозначается 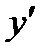 .
.
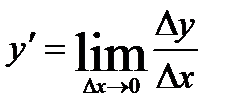 |
Производная производной первого порядка называется производной второго порядка.
y’’=(y’)’
Формулы дифференцирования
1. (С)′ = 0 11. (sin x)′ = cos x
2. (х)′ = 1 12. (cos x)′ = - sin x
3. (u + v – w)′ = u′ + v′ - w′ 13. (tg x)′ = 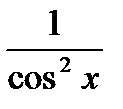
4. (u∙v)′ = uv′ +vu′ 14. (ctg x)′ = 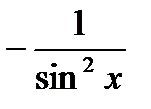
5. (Cx) = C 15. (ln x)′ = 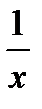
6. (Cu)′ = C(u)′ 16. (lg x)′ = 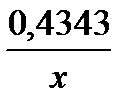
7. (x m)′ = m∙x m – 1 17. (a x)′ = a x∙ln x
8. 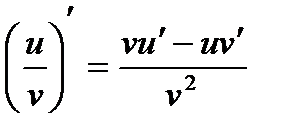 18. (e x)′ = e x
18. (e x)′ = e x
9. 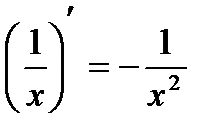 19. (arcsin x)′ =
19. (arcsin x)′ = 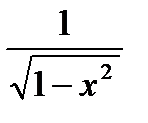
10. ( 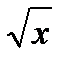 )′ =
)′ = 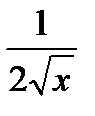 20. (arctg x)′ =
20. (arctg x)′ = 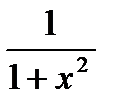
Замечание.Нахождение производной функции называется дифференцированием функции.
Примеры
Продифференцировать функции:
1. у = 2х3 – 4х2 + 5х – 3
Решение.По правилу (3) имеем:
у′ =(2х3)′ - (4х2)′ + (5х)′ – (3)′
Применяя к первым трем слагаемым правило (6), а к последнему – правило (1), получим:
у′ =2(х3)′ - 4(х2)′ + 5(х)′ – 0.
По правилу (5) и (2) имеем:
у′ =2∙3х2 - 4∙2х + 5 ∙1 = 6х2 - 8х + 5.
2. у = (х2 + 1)(2х + 3)
Решение.По правилу (4) имеем:
у′ = ((х2 + 1)(2х + 3))′ = (х2 + 1)(2х + 3)′ + (х2 + 1)′ (2х + 3)
По правилу (3) имеем:
у′ =(х2 + 1)((2х)′ + (3)′) + ((х2)′ + (1)′) (2х + 3)
По правилам (6), (2), (1) и (7)
у′ =(х2 + 1)(2 + 0) + (2х + 0)(2х + 3) =2х2 + 2 + 4х2 + 6х = 6х2 +6х + 2.
3. 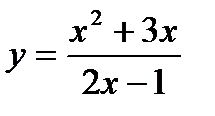
Решение. По правилу (8) имеем:
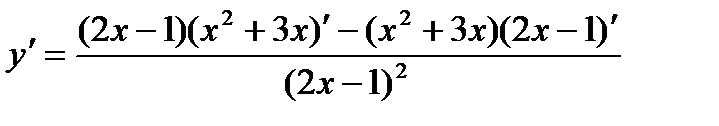
По правилам (7), (5), (1):
= 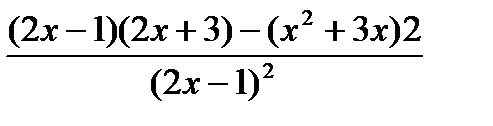
раскроем скобки и приведем подобные: 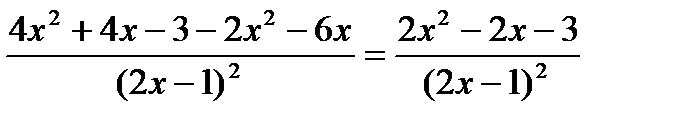 .
.
4. 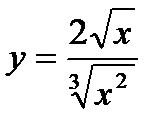
Решение.Упростим функцию:
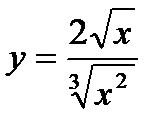 =
= 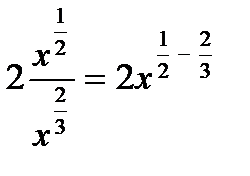 =
= 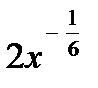
по правилу дифференцирования степенной функции (8) получим
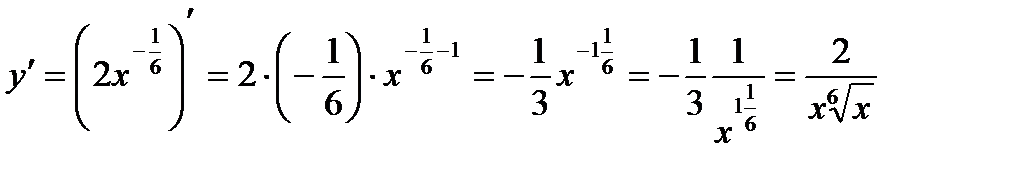
5. 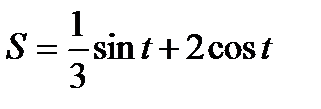
Решение.По правилу (8) имеем:
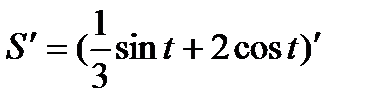 =
= 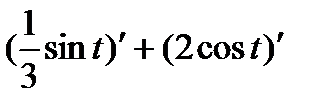 =
=
По правилу (6), (11), (12) имеем:
= 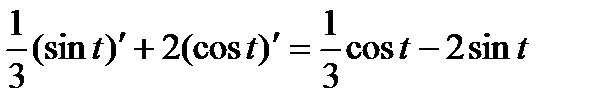
Практическая работа 1
"Дифференцирование функций и построение графиков"
Цель работы: формировать умения по выполнению дифференцирования функций и применению ее к решению задач
Основные понятия
Определение 1.Функция называется простой, если над аргументом выполняется одно функциональное действие.
Определение 2. Функция называется сложной, если над аргументом выполняется более одного функционального действия.
Замечание.Путем замены переменной сложную функцию можно свести к простой, но уже относительно новой переменной.
Например
Производная сложной функции
Производная сложной функции равна произведению производной данной функции по промежуточному аргументу (замене) на производную промежуточного аргумента (замены) по основному.
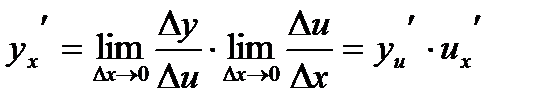 |
(1)
Например. Найти производную функции y = (3x2 – 5)3.
Решение. y’ = ((3x2 – 5)3) ’ Функция сложная.
Заменой переменной обозначимu = (3x2 – 5).
Тогда функция примет вид y = u3.
По (1) ищем ее производную в таком виде: y’ = (u3) ’=3u2∙u’.
Вернемся к старой переменной: y’ = (u3) ’=3u2∙u’ = 3(3x2 – 5)2(3x2 – 5)’
Взяв производную скобки, окончательно получим:
y’ = 3(3x2 – 5)2∙6х = 18х(3x2 – 5)2.
Замечание.
1) Для введения промежуточной переменной u необходимо помнить, что функция должна стать простой, т.е. иметь одно действие. Для этого необходимо разобраться в порядке действий в данной функции, найти последнее и оставить его, т.е. обозначить за u все, что есть, до последнего действия.
2)За u не обозначается постоянное число, помнить, что u – это функция.
3) За u не обозначается все выражение, т.к. тогда не будет ни одного действия.
Например.
1) y = 2(x – 1)5, u = (x – 1) 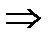 у = 2u5
у = 2u5
2) y = 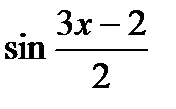 , u =
, u = 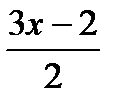
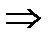 y = sin u
y = sin u
3) 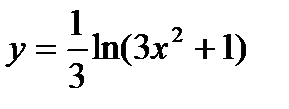 , u =
, u = 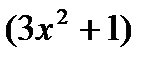
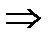 y =
y = 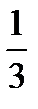 ln u
ln u
Примеры
Продифференцировать функции
1) y = (x3 – 4x + 1)3
Решение
Функция сложная, т.к. над аргументом х выполняется несколько действий. Введем промежуточную функцию u = (x3 – 4x + 1), сводящую данную функцию к простой y = u3.
И тогда, по формуле степенной функции (7) получим:
y’ =(u3)’=3u2∙u’ = 3 (x3 – 4x + 1)2(x3 – 4x + 1)’ =3 (x3 – 4x + 1)2(3х2 – 4)
2) 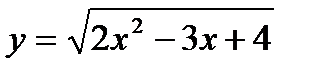
Решение
Функция сложная, т.к. над аргументом х выполняется несколько действий. Введем промежуточную функцию u = 2x2 – 3x + 4,сводящую данную функцию к простой: 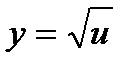 .
.
Тогда, по формуле (10):
( 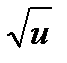 )′ =
)′ = 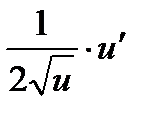 , получим:
, получим:
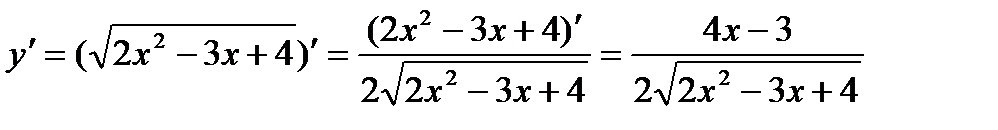
3) 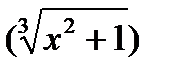
Если дан корень другой степени, то его нужно преобразовать в степень с дробным показателем и затем применить формулу (7).
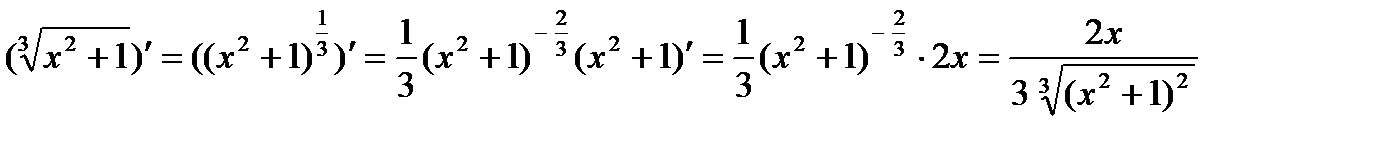
4) 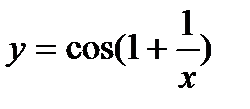
Решение
Функция сложная, введем промежуточную переменную 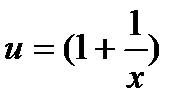 .
.
И по формуле (12):
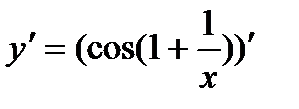
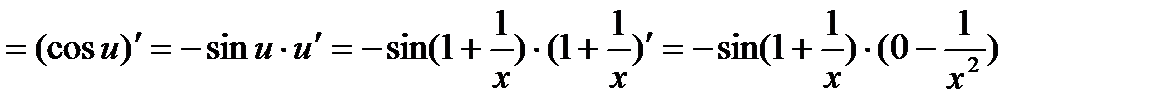 =
=
= 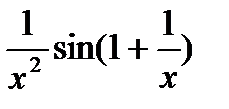
Решение
Найдем момент (время), когда пути, пройденные точками, сравняются, т.е. будут равны: S1 = S2 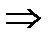 5t2–2t+1 = 5t2–3t+2.
5t2–2t+1 = 5t2–3t+2.
Решая полученное уравнение относительно t, получим t = 1.
По определению физического смысла производной V = (S)’.
Таким образом, найдем формулы для вычисления скоростей каждой точки:
V1 = (S1)’ = (5t2 – 2t + 1)’ = 10t – 2;
V2 = (S2)’ =(5t2 – 3t + 2)’ = 10t – 3.
Тогда в момент t = 1равенства пути найдем скорости каждой точки:
V1 (1) = 10∙1 – 2 = 8;
V2 (1) = 10∙1 – 3 = 7.
По определению физического смысла производной второго порядка ускорение а = (V)’.
Тогда, найдем формулы для вычисления ускорения каждой точки:
a1 = (V1)’ = (10t – 2)’ = 10
а2 = (V2)’ = (10t – 3)’ = 10.
Таким образом, ускорение не завит от времени ни для одной точки и равно 10 в любой момент времени для каждой точки.
2.Точка движется прямолинейно по закону 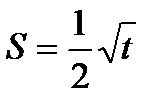 . Найти ее скорость в момент t = 2,25.
. Найти ее скорость в момент t = 2,25.
Решение
1) Найдем скорость по формуле: 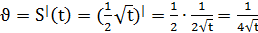
2) Вычислим скорость в момент времени t=2,25
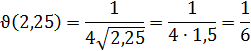
Решение.
1) Найдем скорость
V= 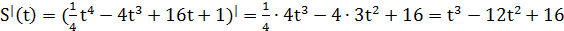
2) Найдем скорость в начальный момент времени
V(0)= 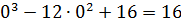
3) Найдем ускорение по формуле:
а=V¢(t)=S¢¢(t)= 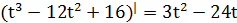
4) Вычислим ускорение в момент времени t=2
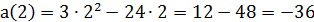
Интеграл и его приложения
Теоретический материал
Имея функцию, можно по известным правилам найти ее производную, то есть продифференцировать. Это имеет большое практическое значение: нахождение скорости, ускорения, уголовного коэффициента касательной и т.п.
Однако часто приходится решать обратную задачу: дана функция f(x), требуется найти функцию F(x) такую, что 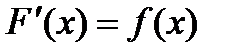 или
или 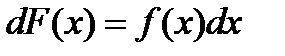 .
.
Для решения обратной задачи служит операция интегрирования, обратная операции дифференцирования.
Функцию F(x) называют первообразной для f(x).
Пример 1. Найти первообразную для функции 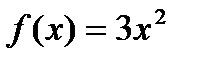 .
.
Такой первообразной является функция 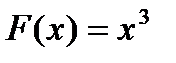 , так как
, так как 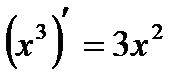 . Но это не единственная первообразная для
. Но это не единственная первообразная для 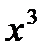 . Также подойдут:
. Также подойдут: 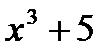 ,
, 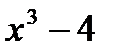 и вообще
и вообще 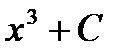 , где С – произвольная постоянная, потому что
, где С – произвольная постоянная, потому что 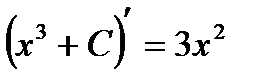 .
.
Пример 2. Найти первообразную для функции 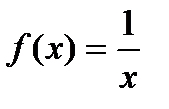 .
.
Первообразной для функции 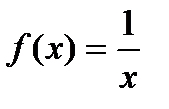 будет
будет 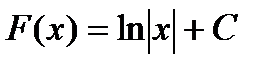 , так как
, так как 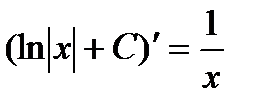 .
.
Пример 3. Найти первообразную для функции 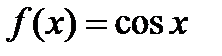 .
.
Первообразной для функции 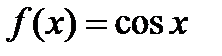 будет
будет 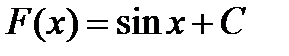 , так как
, так как 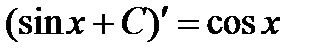 .
.
Определение 1. Функция F(x) + C называется первообразной для функции f(x), если выполняется условие 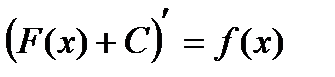 .
.
Определение 2. Множество первообразных F(x)+С, соответствующих данной функции f(x), называют неопределённым интегралом и обозначают символом 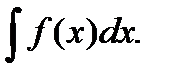
Можно записать: 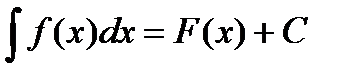 ,
,
где 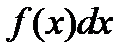 - подынтегральное выражение,
- подынтегральное выражение,
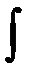 - знак неопределённого интеграла,
- знак неопределённого интеграла,
С – постоянная интегрирования.
Таблица неопределенных интегралов
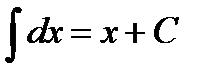 | 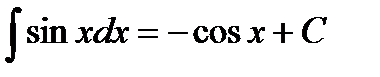 | ||
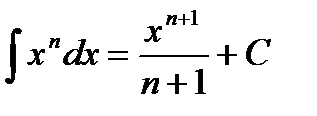 , если n≠1 , если n≠1 | 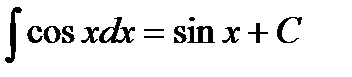 | ||