Матрицы и действия над ними. Умножение матриц.
Матрицы и действия над ними. Умножение матриц.
Матрица – таблица чисел вида -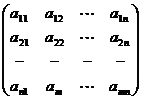 
Если число м не равно н, то матрица прямо – линейная, если равно то квадрат. (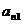 
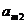
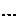
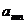) – главная диагональ. Матрица из одной строки – матрица строка. Матрица из одной столбца – матрица столбец. Ноль матрица – все элементы нули. Матрица, у которой на главной диагонали единицы, а остальные нули – единичная матрица, значится Е. В транспонированной 
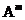, если она получатся из исходной при замене строк на столбцы.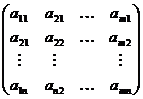 
= 
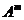=В Сумма двух матриц называется матрица С по формуле: А+В=С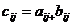 
1)А+В=В+А – коммутативность. 2) (А+В)+С = А+(В+С) – ассоциативность. 3)А+0=А Матрицы можно умножать на число. А*К=В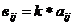 
К – любое число. Произведение матрицы на матрицу. А*В=С 
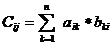Из формулы видно, что произведение возможно только, если число столбцов равно числу строк. Свойство умножения: 1)А*В # В*А – не коммутативность А*В=В*А – коммутативность. 2) (А*В)*С=АС+ВС – дистрибутивность. 3)А*Е=А=Е*А
2. Алгебраические дополнения и миноры. Определители второго порядка и их свойства. Алгебраическим дополнением элемента aij матрицы A называется число Aij = ( − 1)i + jMij, где Mij — дополнительный минор, определитель матрицы, получающейся из исходной матрицы A путем вычёркивания i -й строки и j -го столбца.
Минор. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.
Определителем второго порядка, соответствующим данной матрице, называется число, обозначаемое символом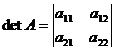 
и определяемое равенством det А = а11а22 - а12а21. Диагональ, образованная элементами а11 и а22 называется главной. Диагональ, образованная элементами а12 и а21 называется побочной. Свойства:1) Определитель не изменится, если его строки поменять местами. 2) Если в определители поменять местами любые 2 строки или столбца, то он изменит свой знак на противоположный. 3) Если строка (столбец) в определителе имеет общий множитель, то этот множитель можно вынести за знак определителя. 4) Определитель с двумя одинаковыми строками (столбцами), равен нулю. 5) Если все элементы какой-либо строки или столбца прибавить элементы другой строки или столбца умноженное на одно и то же число, то определитель не изменится .3. Определители третьего порядка. Вычисление определителя разложением по строке (столбцу). Понятие об определителях n-го порядка.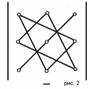 
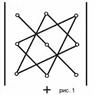
Определитель n-порядка равен сумме попарных произведений элементов какой-нибудь строки (столбца) на их алгебраических дополнений. Замечание: 1)Рекомендуется открывать определитель, где больше нулей. 2)Все свойства определителя 2 порядка справедливы для n-порядка.
Производные основных элементарных функций.
 |  |
 |  |
 | |
 |  |
 |  |
 |  |
 |  |
| |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
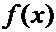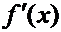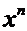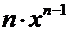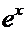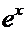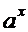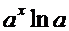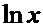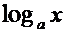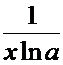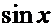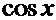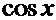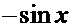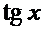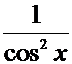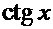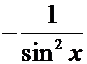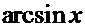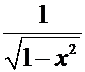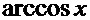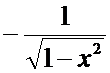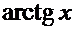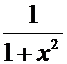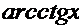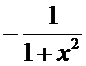Матрицы и действия над ними. Умножение матриц.
Матрица – таблица чисел вида -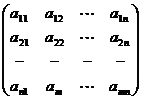
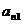
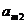
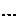
Если число м не равно н, то матрица прямо – линейная, если равно то квадрат. ( 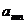) – главная диагональ. Матрица из одной строки – матрица строка. Матрица из одной столбца – матрица столбец. Ноль матрица – все элементы нули. Матрица, у которой на главной диагонали единицы, а остальные нули – единичная матрица, значится Е. В транспонированной 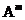, если она получатся из исходной при замене строк на столбцы.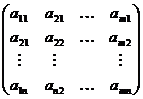 = =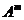В Сумма двух матриц называется матрица С по формуле: А+В=С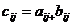
1)А+В=В+А – коммутативность. 2) (А+В)+С = А+(В+С) – ассоциативность. 3)А+0=А Матрицы можно умножать на число. А*К=В 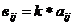К – любое число. Произведение матрицы на матрицу. А*В=С 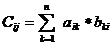Из формулы видно, что произведение возможно только, если число столбцов равно числу строк. Свойство умножения: 1)А*В # В*А – не коммутативность А*В=В*А – коммутативность. 2) (А*В)*С=АС+ВС – дистрибутивность. 3)А*Е=А=Е*А
2. Алгебраические дополнения и миноры. Определители второго порядка и их свойства. Алгебраическим дополнением элемента aij матрицы A называется число Aij = ( − 1)i + jMij, где Mij — дополнительный минор, определитель матрицы, получающейся из исходной матрицы A путем вычёркивания i -й строки и j -го столбца.
Минор. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.
Определителем второго порядка, соответствующим данной матрице, называется число, обозначаемое символом 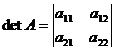и определяемое равенством det А = а11а22 - а12а21. Диагональ, образованная элементами а11 и а22 называется главной. Диагональ, образованная элементами а12 и а21 называется побочной. Свойства:1) Определитель не изменится, если его строки поменять местами. 2) Если в определители поменять местами любые 2 строки или столбца, то он изменит свой знак на противоположный. 3) Если строка (столбец) в определителе имеет общий множитель, то этот множитель можно вынести за знак определителя. 4) Определитель с двумя одинаковыми строками (столбцами), равен нулю. 5) Если все элементы какой-либо строки или столбца прибавить элементы другой строки или столбца умноженное на одно и то же число, то определитель не изменится .3. Определители третьего порядка. Вычисление определителя разложением по строке (столбцу). Понятие об определителях n-го порядка.
Определитель n-порядка равен сумме попарных произведений элементов какой-нибудь строки (столбца) на их алгебраических дополнений. Замечание: 1)Рекомендуется открывать определитель, где больше нулей. 2)Все свойства определителя 2 порядка справедливы для n-порядка.