В коробке лежат 4 голубых, 3 красных, 9 зеленых, 6 желтых шариков. Какова вероятность того, что выбранный шарик будет не зеленым?

A. 13/22;

В лотерее 1000 билетов, среди которых 20 выигрышных. Приобретается один билет. Какова вероятность того, что этот билет невыигрышный?

C. 0,98;

Имеется 6 учебников, из которых 3 в переплете. Наудачу берут 2 учебника. Вероятность того, что оба взятых учебника окажутся в переплете составляет…

A. 0,2;

В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу выбирают 3-х человек. Вероятность того, что все отобранные будут мужчинами составит …

A. 0,3;

В ящике 10 шаров, из которых 6 окрашенных. Наудачу извлекают 4 шара, не возвращая их. Вероятность того, что все вынутые шары окажутся окрашенными, составляет…

B. 0,071;

В ящике 4 красных и 2 синих шара. Из него наудачу берут три шара. Вероятность того, что все эти три шара – красные, равна…

A. 0,2;

Монету подбрасывают 100 раз. Вероятность появления решки 0,42. Сколько раз выпала решка?

A. 42;

Студент знает 20 вопросов из 25 вопросов по дисциплине. Ему предлагают 3 вопроса. Вероятность того, что студент знает их, составляет…

C. 0,495.

В урне 4 белых и 3 черных шара. Одновременно вынимают два шара. Вероятность того, что оба шара белые, составляет…

C. 2/7.

Бросают 3 кубика сразу. Вероятность того, что выпадут 3 шестерки, составляет…

C. 1/216.

Участковый врач в течение недели принял 35 пациентов, из которых пяти пациентам был поставлен диагноз – язва желудка. Определите относительную частоту появления на приеме пациента с заболеванием желудка.

C. 1/7.

В урне находится 6 белых, 9 черных и 5 красных шаров. Какова вероятность вынимания красного шара?

A. 0,25;

Определить относительную частоту заражения гриппом, если из 20 человек, находившихся в контакте с больным, здоровыми остались 8.

A. 0,4;

На приеме у участкового врача в течение недели побывало 72 человека, из которых 16 пациентам был поставлен диагноз - бронхит. Определить относительную частоту появления на приеме пациента, больного бронхитом.

A. 0,22

Определить вероятность выпадения при бросании игральной кости числа очков, меньшего 5.

C. 4/6;

Определите вероятность выпадения нечетного числа очков при бросании игральной кости.

D. 0,5.

События A и B противоположные, если P(A)=0.4 , тогда P(B)=

B. 0,6;

Если события A и B несовместимые и P(A)=0.2 а P(B)=0.05 , то P(A+B)=

A. 0,25;

Если P(B/A)=P(B), то события A и B:

C. зависимые;

Условная вероятность события A при условии B записывается в виде:

D.

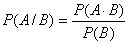Если P(AB)=0.35 и P(B)=0.7 , то P(A/B)=

C. 0,5.

Если вероятность события A не зависит от того, произошло ли событие B или нет, то P(A) и P(B) являются:

A. безусловными;

События называются зависимыми

D. если появление одного из них влияет на появление другого.

Гипотезами называют события, которые

A. являются независимыми и образуют полную группу;

Вероятность произведения двух зависимых событий равна

A. произведению вероятностей первого из них на вероятность второго;

Условной вероятностью события А называется

A. вероятность события А, вычисленная при условии, что вероятность события В приняла определенное значение;

Случайные величины могут быть

C. либо дискретными, либо непрерывными;

Относительной частотой случайного события называется величина, равная

A. отношению числа случаев, благоприятствующих событию к общему числу равновозможных, несовместных событий;

B. пределу, к которому стремится отношение числа случаев, в которых реализуется событие, к общему числу испытаний при неограниченном увеличении числа испытаний;

C. отношению общего числа испытаний к числу испытаний, в которых реализуется событие A.

Случайная величина – это величина

C. явление, которое при совокупности одних и тех же условий может произойти, а может не произойти;

Дискретная случайная величина:

A. число операций в день;

D. число вызовов на станцию скорой помощи за 1 час.

Выберите верные утверждения о дискретной случайной величине:

B. вероятность появления конкретного значения величины Х равно нулю;

C. величина принимает конечное или счетное множество значений;

Какие из приведенных примеров определяют, как случайную величину?

B. вес студента;

Какая характеристика имеет смысл среднего значения случайной величины?

D. математическое ожидание.